循环神经网络(RNN)的例子与他的训练算法
RNN
在经历了前馈网络的直线结构，接下来我们要学习的就是循环神经网络的自环结构，这种结构的优点是能够短时记忆并且在能在这段时间内训练参数，实现自动学习的功能，同时过程中神经网络有了记忆能力。在处理目标检测时与CNN组成为R-CNN网络，自然语言处理中也使用RNN处理上下文有关联的文本，其中主要使用LSTM模型。
拓扑结构
首先我们需要知道RNN的结构是什么样的，既然他是自环的传递的，单个神经结构是这样的，每个部分都有两个节点，一个负责处理输入。一个负责反馈输出，后者叫记忆体。
注意，本文的公式形式与其他博文不同，要注意U、W、V的位置，避免记错
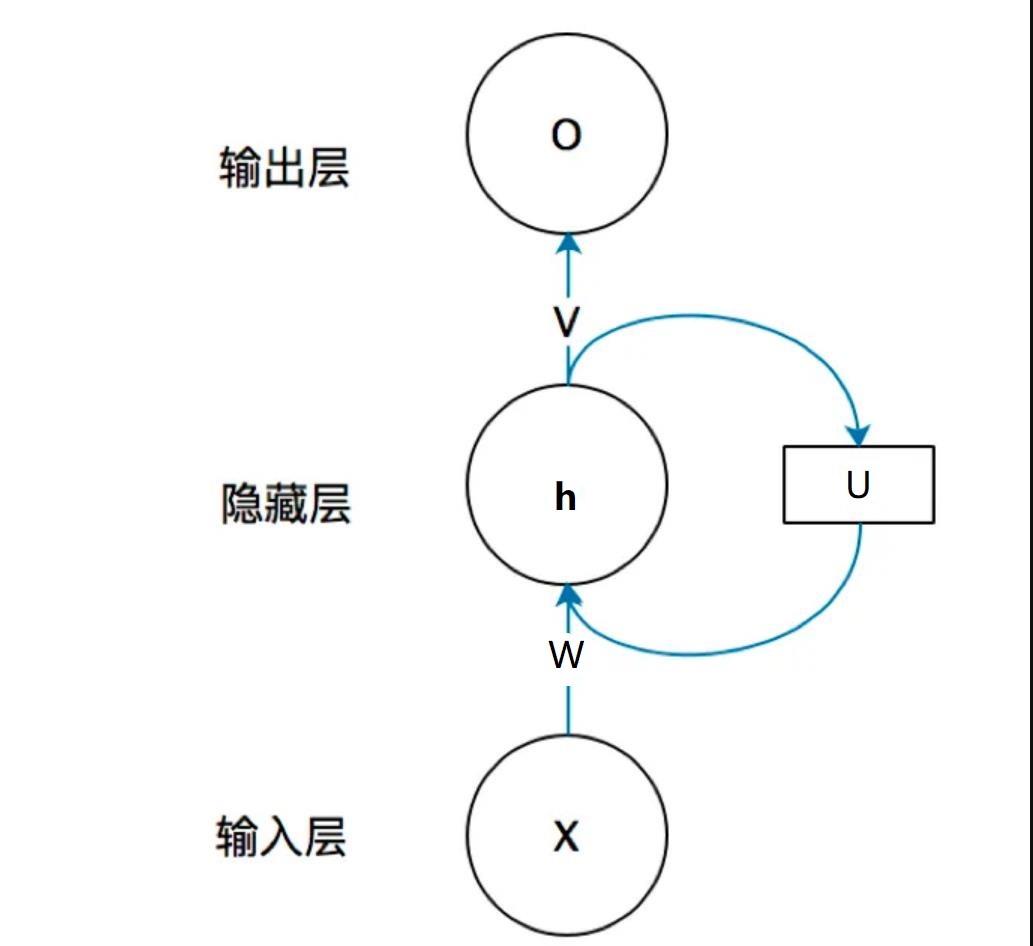
如果在时间尺度上对RNN展开，就得到了一个直线型的结构：
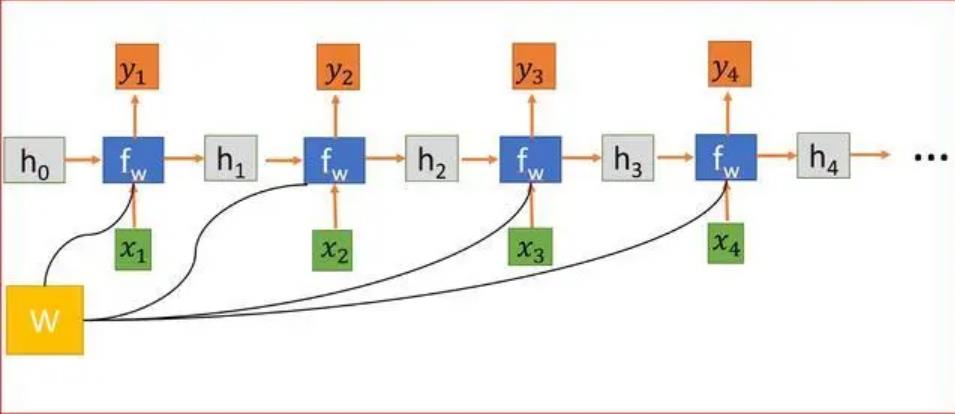
第一个图片中w表达的是记忆体的矩阵，在第二个图中h表达为f的输出和w组成的函数，这个函数是马尔可夫的。
在NLP中最关键的一步就是word2vec，这类算法很多，比如贝叶斯或者特征提取网络，最终都会将内容转化一个向量序列，这个1向量序列就是神经网络的输入。我们将他写作$\vec x=(x_1,x_2,…,x_n)$，这样学习体h与时间t作为角标之间有关系，f为一个激活函数，一般为sigmoid。
$$
h_t=f(z_t)
$$
其中我们的$z_t$等于如下形式：
$$
z_t=Uh_{t-1}+Wx_t+b
$$
而输出有：
$$
o_t=Vh_t+c
$$
训练
既然我们了解了他的结构那我们肯定要去学习如何训练这个网络，首先我们需要分析，这种结构的本质上还保留了前馈神经网络的特性，所以我们依然可以使用反向传播算法进行训练，可是由于每个单元都具有两个函数，并且这个函数是马尔可夫的，所以我们需要在训练时加入时间产生的因素。这样我们就有了BPTT（随时间进行的反向传播）算法。
BPTT
首先我们需要一个损失函数L，我们让损失函数关于前一时刻的输出进行建立关系：
$$
\frac{\partial L}{\partial u_{ij}}=\sum_{k=1}^t\frac{\partial L}{\partial z_k}\frac{\partial z_k}{\partial u_{ij}}
$$
解释一下这个微分，他表达损失函数关于第ij个循环节点的参数的偏微分，因为循环神经网络是有时间关系限制，所以我需要将所有时间的链式法则进行加和，最后就是基本的链式法则表达时刻t节点(i,j)的微分。为了包含进所有记忆体，我们将链式结构在时间上展开：
$$
\frac{\partial L}{\partial z_k}=\frac{\partial h_k}{\partial z_k}\frac{\partial z_{k+1}}{\partial h_k}\frac{\partial L}{\partial z_{k+1}}
$$
为了便于表示我们定义一个误差变量，它的计算依然是链式法则，写出对应项即可：
$$
\delta_k = \frac{\partial L}{\partial z_k} = Ef’(z_k) U^T \delta_{k-1}
$$
其中E是单位矩阵，负责把激活函数的导数值变成矩阵形式（导数值应为向量），这样我们可以有最终的计算公式：
$$
\frac{\partial L}{\partial U}=\sum_{k=1}^t\delta_{t,k}h_{t,k-1}^T
$$
$$
\frac{\partial L}{\partial W}=\sum_{k=1}^t\delta_{t,k}x_{k}^T
$$
$$
\frac{\partial L}{\partial b}=\sum_{k=1}^t\delta_k
$$
关于输出过程的迭代可以很容易的计算：
$$
\frac{\partial L}{\partial V}=\frac{\partial L}{\partial o_t}h_t^T
$$
$$
\frac{\partial L}{\partial b}=\frac{\partial L}{\partial o_t}
$$
这样我们就有了最基本的训练算法，当然如果对时间效率追求不高，可以使用实时反向传播，不过无法计算出可以使用的梯度，所以此法一般用于在线学习。
长程依赖问题
为了防止RNN在计算过程中出现梯度消失或者梯度爆炸的问题，因为BPTT是包含了时间作为角标的，如果时间尺度过大就会导致梯度非常大，如果两次训练是相差瞬时，那么就会出现梯度消失，为了必满这种情况发生，可以采取以下几种办法：
1、梯度爆炸就衰减，对相关参数进行l1或l2正则化限制参数的取值范围，让他能够即使的截断时间。
2、梯度消失让记忆体的输出更大，通过改变U的大小就可以，但是会出现李毅中梯度爆炸的情况，当然也有h积累过多造成的记忆容量溢出的问题
为了有效解决这些办法，可以使用门控循环神经网络，代表为长短期记忆网络(LSTM)
LSTM
为了保证能够拥有记忆时效，我们需要重新整理一下节点的结构，他需要一个输入(output)，一个输出(input)和一个遗忘(forget)，我们把这三部分都用门控表示，得到：
$$
i_t=\sigma(w_ix_t+U_ih_{t-1}+bi)
$$
$$
f_t=\sigma(w_fx_t+U_fh_{t-1}+b_f)
$$
i为输入门，f为遗忘门，我们计算：
$$
\hat C_t = tanh(W_cx_t+U_ch_{t-1}+b_c)
$$
然后使用上一时刻的C计算当前时刻的C：
$$
C_t=f_tC_{t-1}+i_t\hat C_t
$$
最后我们整合输出信息得到：
$$
o_t=\sigma(w_ox_t+U_oh_{t-1}+bo)
$$
$$
h_t=o_ttanh(C_t)
$$
我们很容易就看出来，这种门控结构对输出内容进行了有效的限制，这样每个神经元结构就变成了这样(画了半天，真难受)
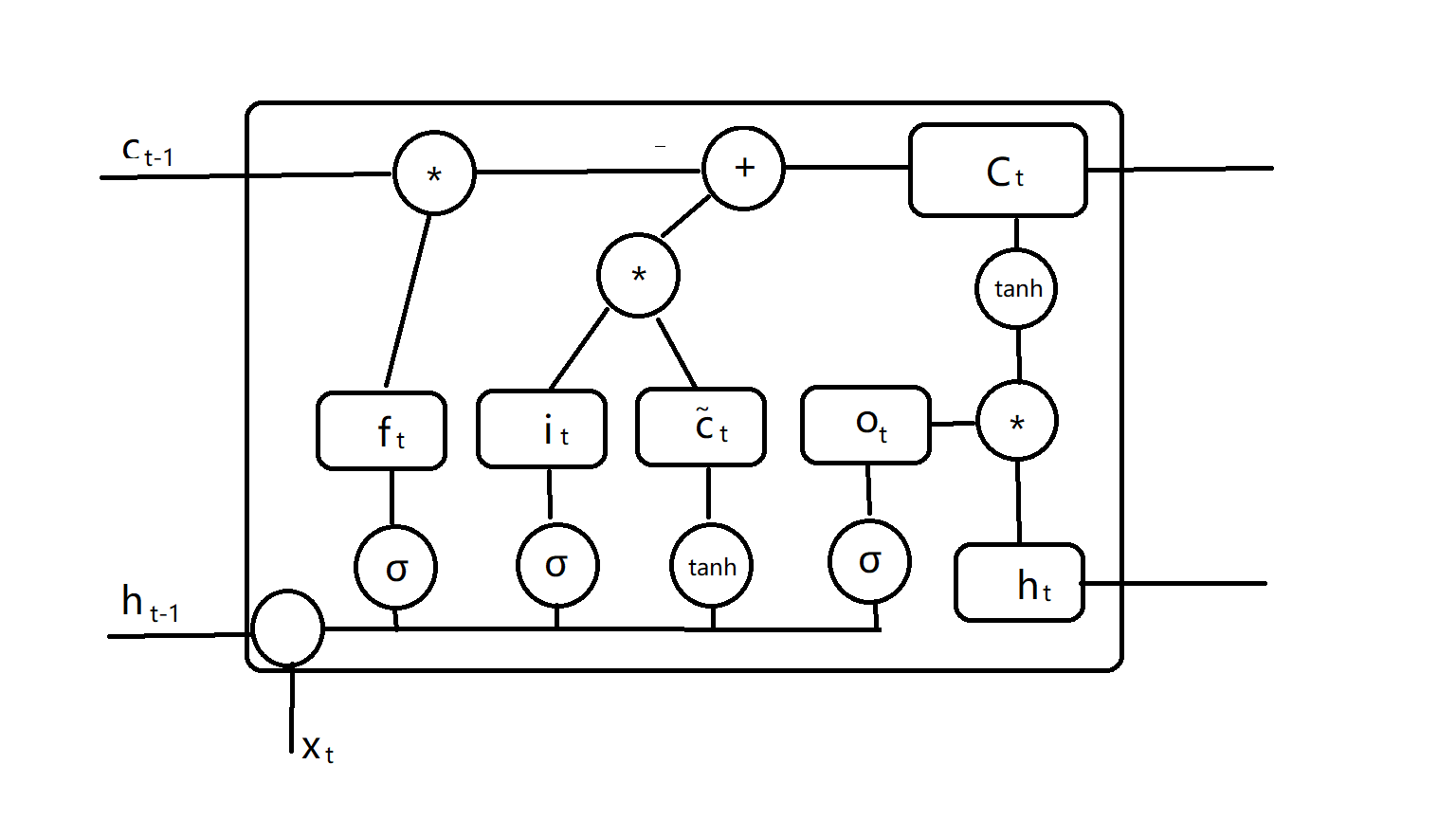
c是对状态的控制，实际上LSTM仍然可以使用BPTT进行训练。在处理输入时能够同时限制学习程度，非常好的解决了长程依赖的梯度爆炸和梯度消失问题。
扩展
堆叠循环网络：将多个循环神经网络首尾相接得到的神经网络
双向循环网络：将两个神经网络互相反向合并，得到的神经网络
总结
循环神经网络凭借它能够有一定记忆的能力，在自然语言处理中能发挥异彩，尤其是在对于前后文有关联的问题上，LSTM更能够解决这类问题。
通过本文学习，读者可以清晰的了解到RNN的结构，了解到BPTT对RNN的训练过程，读者在阅读完成之后可以参考其他的文献，使用tensorflow或者pytorch实现一个RNN来解决一些实际问题，当然在学习了解到LSTM后，在自然语言处理方面也可以如鱼得水，相信此文章会帮助到更多有需要的人。