关于脉冲神经网络的数学原理
介绍
脉冲神经网络(Spiking Neural Network,SNN)是第三代神经网络,从第一代的MP结构到第二代使用BP算法计算的全连接神经网络,现在的第三代模拟神经突触信号的脉冲神经网络。
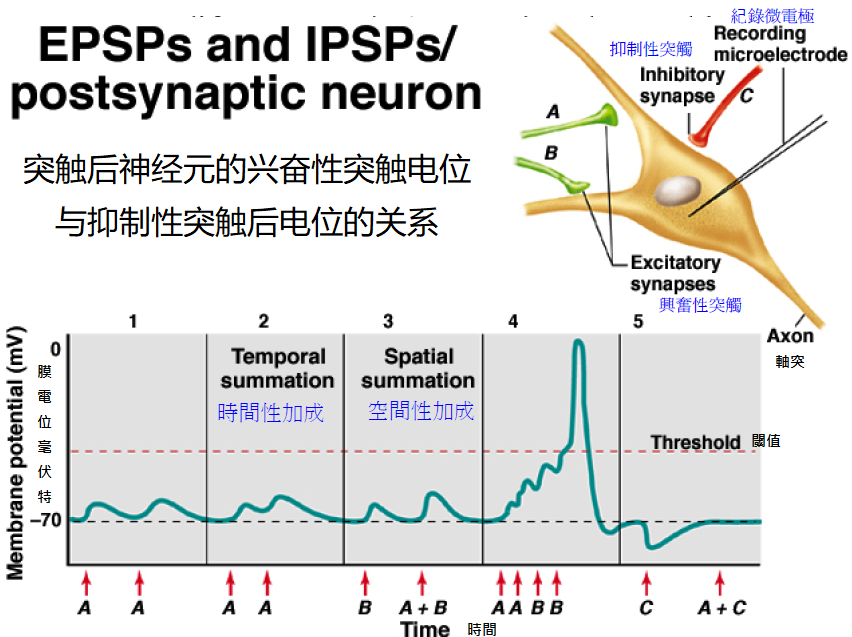
从图里分析,A与B都是兴奋性突触,每次神经递质的传递都会产生一次上升沿,且波动是可加的,在四部分同时传递了四次兴奋信号后,突触后神经元也兴奋了,相对的最后一次的抑制性信息使信号出现下降沿。所以从图上分析,神经的兴奋不仅可以包含时间,也包含空间,所以一个神经元具有编码时空的能力。
为了模拟这种效果,SNN使用了LIF模型,下面是关于ANN与SNN的结构区别,我们可以罗列以下区别:
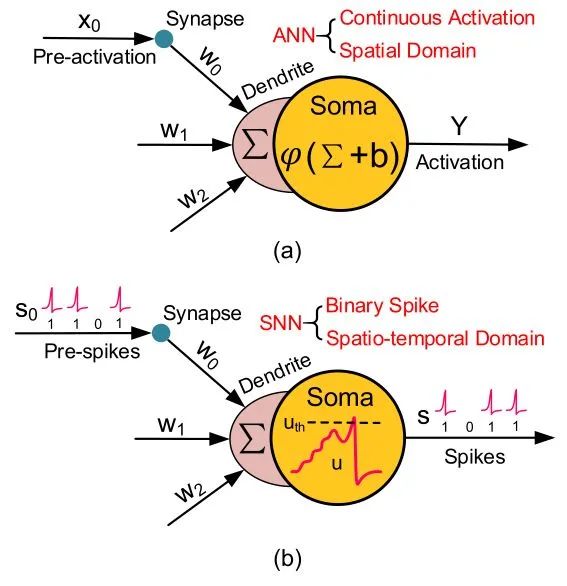
- 激活方式的区别:ANN使用激活函数而SNN使用阈值
- 信号的区别:ANN输出为值而SNN输出为向量信号
- 模型的区别:ANN使用MP模型,SNN使用LIF模型,前者形式更为简单
LIF模型
既然这是一个突触模型,自然要有相似的图像,我们将膜电势u(t)与自身的循环值结合起来就有:
I(t)表示外部刺激对神经的输入,u(t)表示t时刻的膜电压,$\tau$是一个时间常数,在前向传播的过程中,数据在空域(SD)进行传播,同时在时域(TD)产生一个持久的信号,这样就可以有持久的编码。为了得到电势的更新规则,我们让前一刻的电压与后一刻的电压相等,也就是$u(t)|_{t=t-1}=u(t-1)$。
解得:
有了状态更新的过程我们需要前向传播了,对于LIF模型是不需要偏置的,所以只需要一个权重向量即可:
解释以下参数:$x_i^{t+1}$表示t+1时刻第i层n个节点的输出,$\sum_{j=1}^{n-1}w_{i,j}o_j^{t+1}$表示t+1时刻n-1层所有节点的输出组成的向量与第i层的权重向量的乘积,结果是向量。l(n-1)表示的是这一层的节点个数。
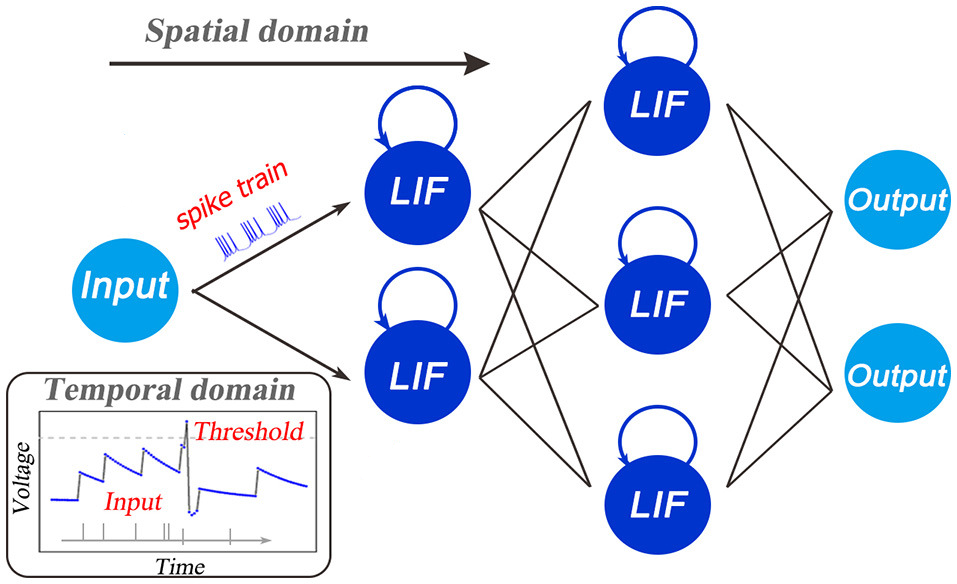
从SNN的结构来看与RNN相似,为了避免长程依赖问题,这里借用了LSTM的公式结构,也就是提供了门控机制。
所以加入了一个非易失性集成(不会被丢失的重复输入),这一步负责更新记忆体u,这里和上文所述的神经元状态方程的解是一个格式的。所以:
自然,这里也需要激活函数:
注意!因为LIF模型的输出是向量,所以不可以用传统的sigmoid或者tanh,而是使用了指示函数进行阈值激活,当值大于某阈时为1,否则为0。
训练
这里可以参考BPTT算法,提出STBP算法,为了方便计算,这里还是使用均方差作为损失函数:
因为计算时需要考虑到所有时刻,所以需要$\frac{1}{T}\sum_t^To_s^t$进行计算输出的平均值。我们简单求个导数:
其中s属于SD,T属于TD。从此我们可以发现,时域和空域是交叉的,我们自然需要考虑时间对传播的影响,所以我们需要针对时域进行分类讨论:
末时刻(t=T)
- 处于最后一层时:
根据链式法则,我们可以得到关于
这个值就是我们之后需要用于更新参数的值,具体如何做可以在下文看到。
- 处于其他层的时候(第n层,n<N):
这个时候就需要考虑空间的因素了,所以上标层数,上标即为时空因素。稍微解读一下,我们需要向前更新一层,就需要用这层的梯度和之前的δ相乘,所以我们需要求出层内所有这样的值进行相加。经过求导法则可以化简形式。
其他时刻(t<T)
- 处于最后一层时:
因为时间状态发生了改变,所以我们需要在时域内进行传播,利用间接求导+直接求导可以写出:
其中$\frac{\partial L}{\partial o_i^{T,N}}$不变,可以直接代入。
- 处于其他层的时候:
在这种情况下,我们需要同时考虑时空因素,而就之前的推断来看:时域需要直接导数加间接导数,空域需要累加所有节点,所以可以写出:
同理也可以计算关于状态的导数,依然使用上述的规则:
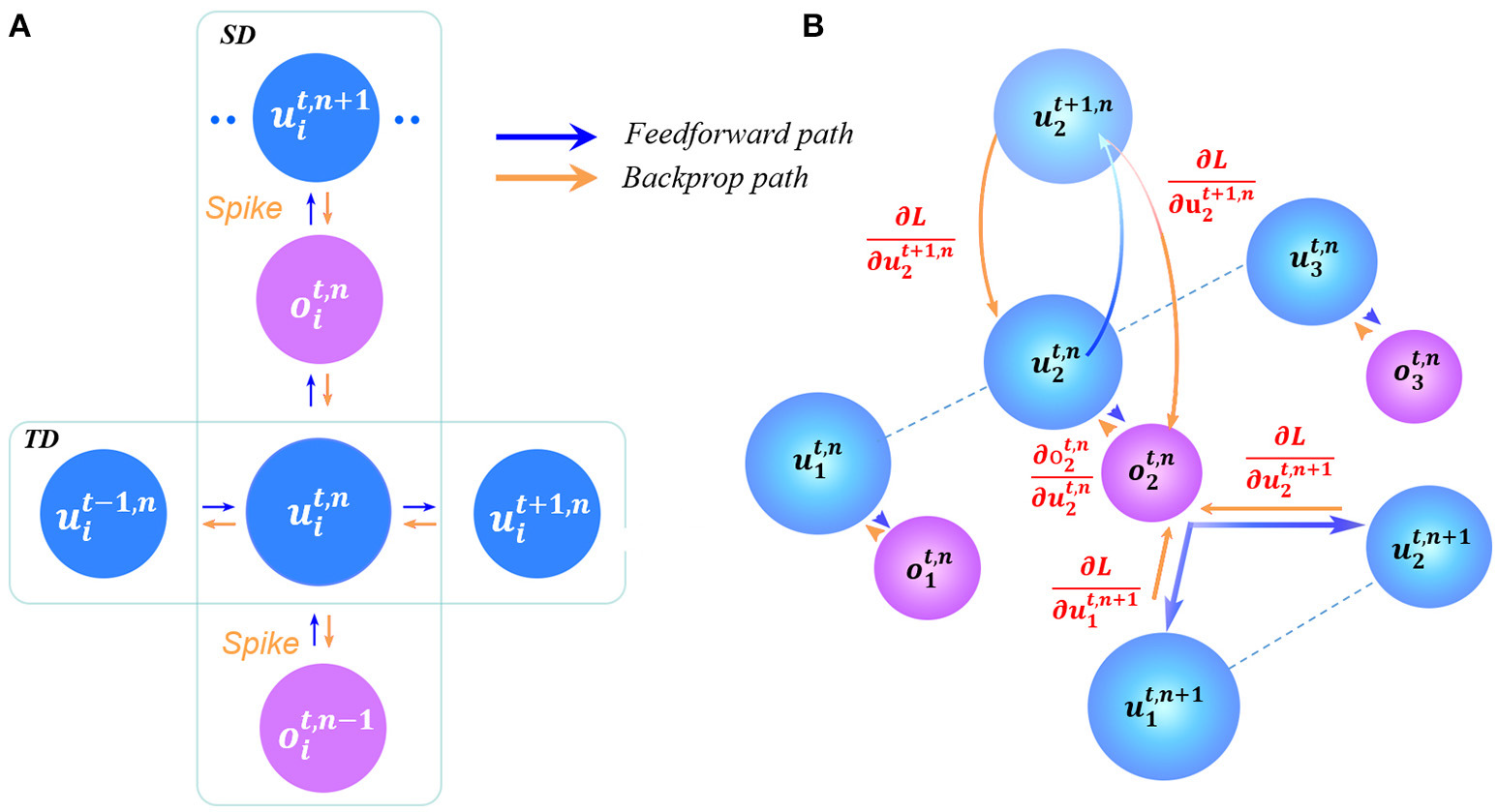
参数更新
自然我们如果要更新权重,我们只需要:
这里省略了状态更新的导数计算过程,不过无非是一个常数项,计算很容易,就结果来看应该为一个矩阵,而从状态更新来看,偏置梯度为:
结果为一个向量,对应当前层各个节点的值。计算过程都不难。从结果来看,g是一个不可微分的函数,我们需要进行一个近似计算,下面是论文提出的相关函数,使用h表示:
$V_{th}$就是阈值,a是一个极小量。
可以看到h3与逻辑函数十分相似,其实就是sigmoid形式的导数。
以上内容均满足:
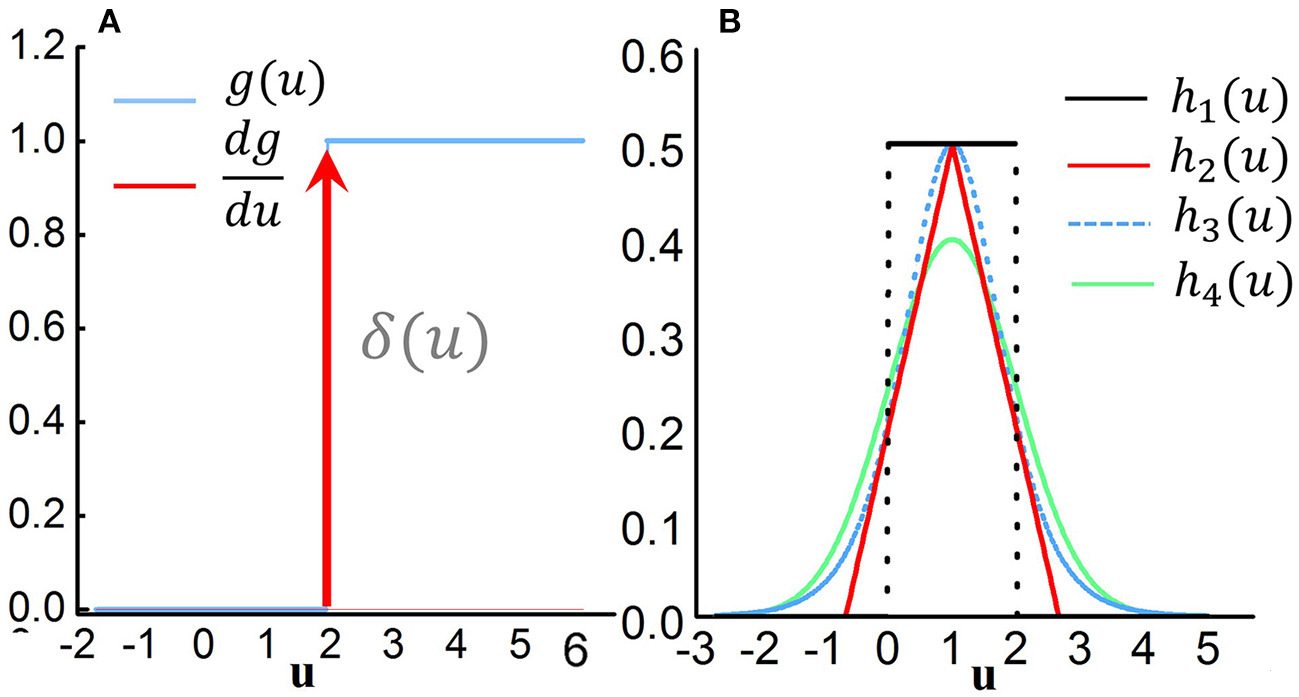
而关于这些函数的训练精度可以参考下图,其中a的取值影响了拟合速度
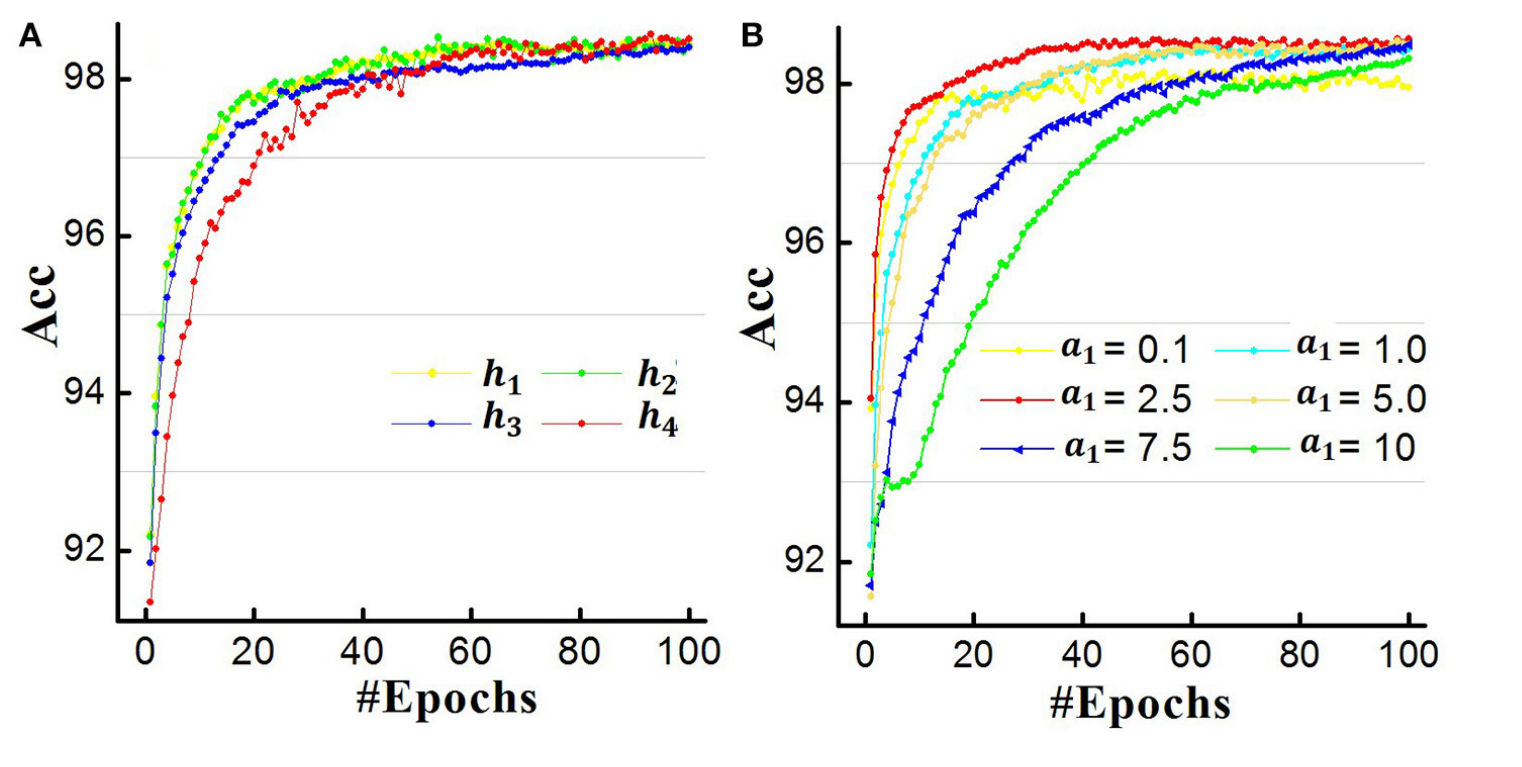
总结
学完脉冲神经网络之后,接下来就是类脑计算领域了,接下来可能就会范围更广,所以需要更加耐心去学习了!
通过阅读本期博文,读者可以学到脉冲神经网络的结构和传播方式,以及参数更新,读者可以重写Tensorflow的layer类实现SNN的计算和参数更新。