关于玻耳兹曼机的数学原理
介绍
玻尔兹曼机是一种使用玻尔兹曼常数定义的价值函数作为训练函数的模型，他的价值函数是马尔可夫离散的，所以为了让利益最大化，我们需要一个似然函数去估计权重。
首先我们必须知道为什么玻尔兹曼机不能使用反向传播进行训练，要知道，前馈神经网络结构都是有向图，而玻尔兹曼机是无向图，也就意味着他并没有方向，自然无法使用反向传播，那么我们先复习一下反向传播
复习BP
我们绘制一个前馈神经网络的结构图，这里为了描述比较简单，我只使用了一条通路，规定x为输入值，y为实际输出值，$\hat y$ 为理论输出值为了衡量我们结果的准确程度，我们需要定义一个损失函数：
$$
L(y,\hat y)=\frac{1}{2}\sum_n(y-\hat y)^2
$$
这里使用的很像协方差的计算方法，有一个关键的区别就是系数不同，这里所选用的$\frac{1}{2}$是为了求导之后能消去，提高计算的简洁。
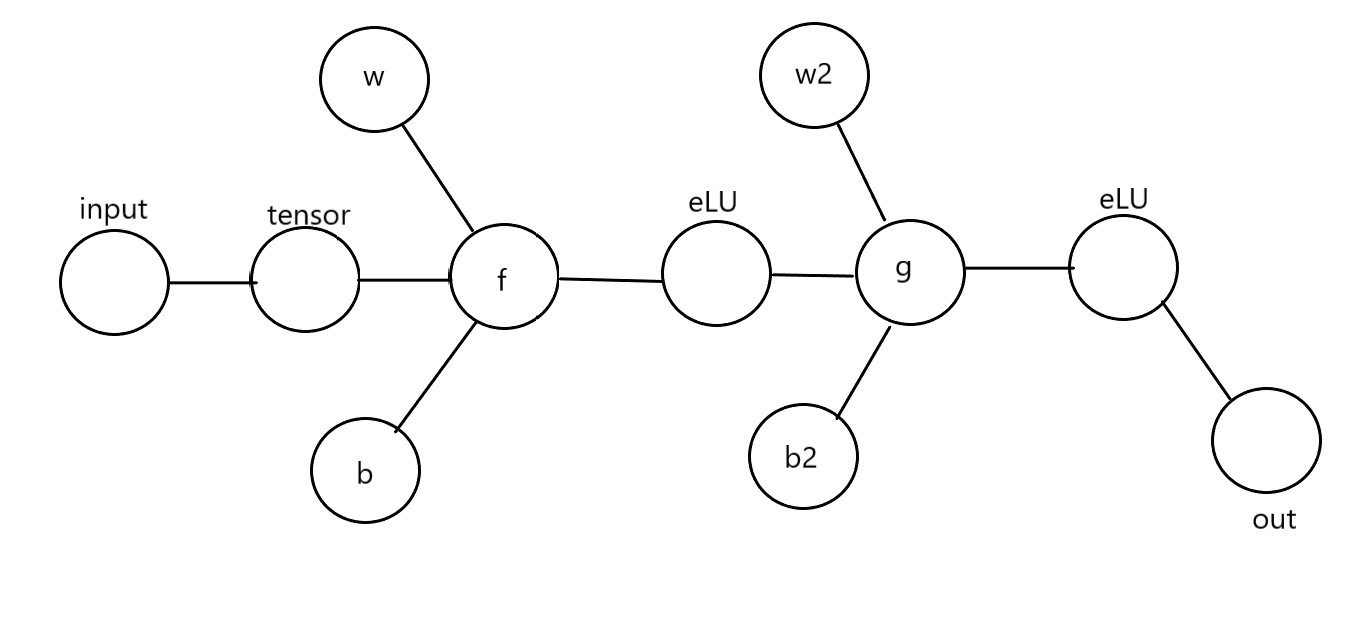
所谓的反向传播，我们把整个传播的过程看作是一个多元函数的运算，然后我们针对某些值求出对应的偏导数。对于结果而言，我们有：
$$
\frac{\partial L}{\partial x} = \frac{\partial L}{\partial \hat y}·\frac{\partial \hat y}{\partial x}
$$
这个过程，我们可以打开$\hat y$这样我们就可以细化为多个导数乘积的形式了：
$$
\frac{\partial L}{\partial w2} = \frac{\partial L}{\partial g}·\frac{\partial g}{\partial w2}
$$
首先我们计算前部分$ \frac{\partial L}{\partial g}$这里我们结合损失函数的定义可以得到：
$$
\frac{\partial L}{\partial g} = \frac{\partial(\frac{1}{2}\sum_n(y-\hat y)^2)}{\partial \hat y}=y(y-\hat y)
$$
后半部分我们很容易求出等于：
$$
\frac{\partial g}{\partial w2} = f
$$
所以最后的结果只需乘法运算即可，这样我们就求出了损失关于某一参数的梯度，这样我们就可以使用注入Adam方法，动量法进行参数学习了。
受限玻尔兹曼机与玻尔兹曼机
玻尔兹曼机本质上是一种概率分布规则，他与反向传播的目的一样，都是通过求函数梯度进行更新，不过玻尔兹曼并未使用损失函数，而是使用似然函数。对比两种玻尔兹曼机的名字，我们发现其实大同小异，无非是多了受限二字，我们看看两者的拓扑结构：
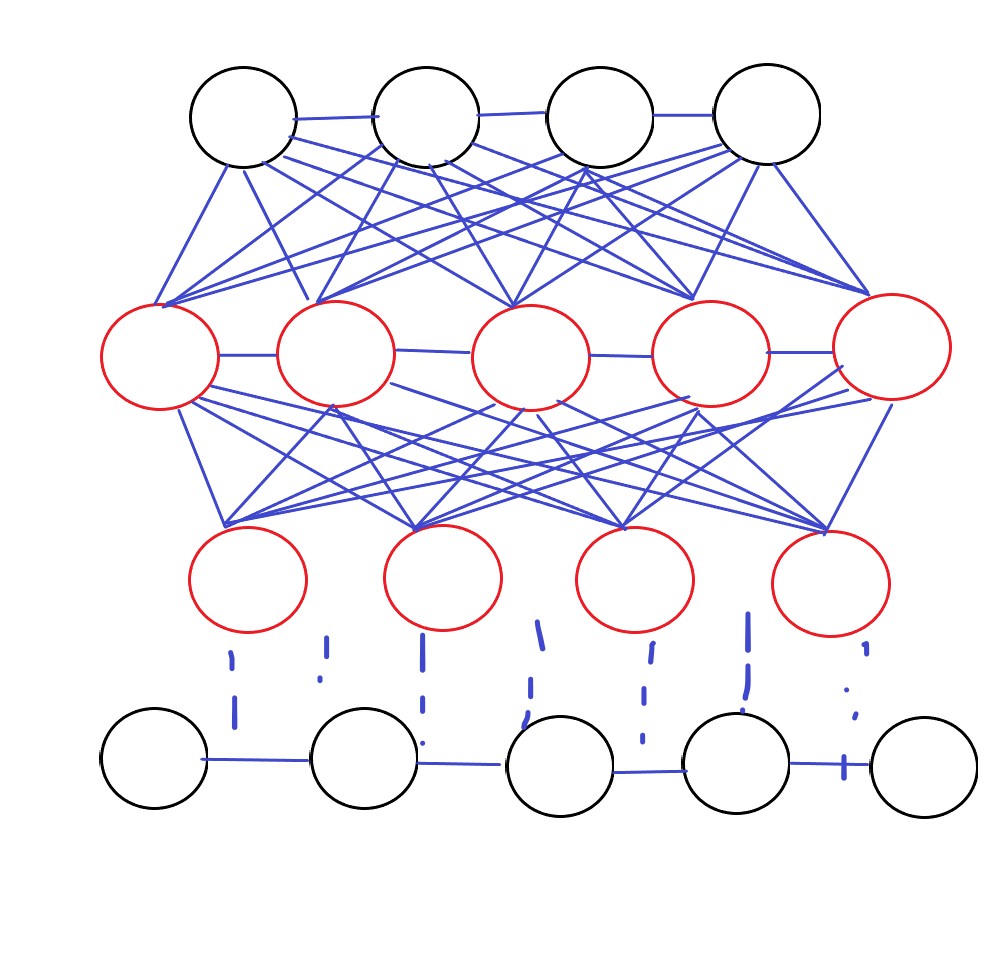
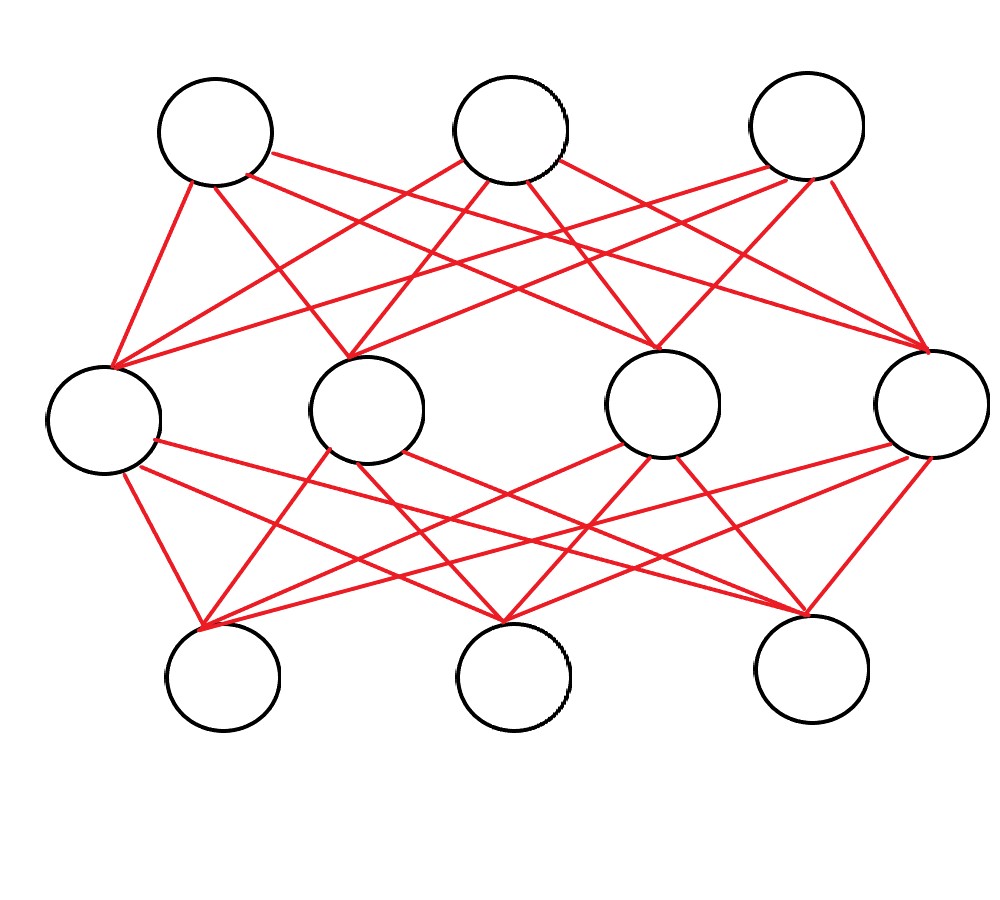
我们看到受限玻尔兹曼机并没有同层结点的连接，也就意味着同层之间不可以进行迭代计算，为了防止同层死循环，所以放弃了同层连接。玻尔兹曼机的训练过程可以使用以下几步：
- 随机初始化各节点的权重和偏置
- 计算出结果并输出
- 使用似然函数修正权重
我们定义似然函数$p(x|\theta)=\prod_n p(x_n|\theta)$，其中的$\theta$可以表示权重或偏置中任意一个量。此条件分布满足玻尔兹曼分布，所以我们可以写出：
$$
p(x_n|\theta)=\frac{1}{Z(\theta)}exp(-E(x,\theta))
$$
E是能量函数，Z为归一因子，两者分别写作：
$$
Z(\theta)=\sum_x exp(-E(x,\theta))
$$
$$
E(x,y)=-\sum_ia_ix_i-\sum_jb_jy_j-\sum_i\sum_jx_iw_{ij}y_j
$$
当然能量函数用矩阵方程写起来更舒服。不过效果等价。不过因为这个函数是带有指数形式的，我们可以把他拆成对数函数，也就是：
$$
ln,p(x_n|\theta)=E(x,\theta);ln,Z(\theta)
$$
当然这不是我们所需要的，我们对参数求导，得到最终结果为：
$$
\frac{\partial ln,p(x)}{\partial w_{ij}}=P(\theta_j=1|x)x_i-\sum_{x}P(x)P(\theta_j=1|x)x_i
$$
$$
\frac{\partial ln,p(x)}{\partial a_i}=x_i-\sum_xP(x)x_i
$$
$$
\frac{\partial ln,p(x)}{\partial b_j}=p(\theta_j=1|x)-\sum_xp(x)p(\theta_j=1|x)
$$
以上这些就是玻尔兹曼机使用的函数，学习算法不变，只是计算梯度的途径发生了改变。
对受限玻尔兹曼机而言，我们就需要对它进行分层（可见层v和隐藏层h），使用方法类似于玻尔兹曼机，我们对能量函数稍作修改即可。
$$
E(v,h)=-\sum_ib_iv_i-\sum_jc_jh_j-\sum_i\sum_jv_iw_{ij}h_j
$$
训练方法同上，仅需换参数即可，这样我们就完成了参数的学习。
应用
如果多层受限玻尔兹曼机堆叠起来会变成什么呢？答案就是一种新的神经网络结构，他就是深度信念网络（DBN），这是一种区别与前馈结构的新结构，它使用的是无向图，目前主要使用的神经结构有：前馈神经网络、循环神经网络、对抗神经网络、级联神经网络、玻尔兹曼机。信念网络主要是利用分布函数或者似然函数进行更新的模型网络，他们共同的特点就是都为无向图。
DBN主要是受限玻尔兹曼网络(RBN)和sigmoid信念网络(SBM)堆叠而成，拓扑结构如下：
对于RBM我们可以使用上文的几个公式最大化似然函数值，尽可能提高可见节点的分布真实性，但在DBN中我们会有贡献度分配的问题，所以我们必须想办法转化SBM为RBM进行学习，然后按照区间逐层训练最后得到结果。
我们给出逐层训练的公式：
$$
p(h_n|h_{n-1})=\sigma(w_nh_n+b_n))
$$
或者使用交替苏醒的方法:
- Wake：从外界输入并自下而上认知，计算每层的后验概率，通过修改参数使后验概率最大化
- Sleep：自上而下认知，计算后验概率，向上修改权重让其最大化
最后我们复习一下概论的两个名词：
先验概率：从原因推结果发生概率
后验概率：从结果推因素的概率
总结
本次博文主要讲了玻尔兹曼机为代表的信念网络，同时复习了反向传播的过程，通过阅读本文，读者可以详细的了解到概念、计算公式以及应用场景。