超声波无源相控阵雷达

基础

有源相控阵雷达是R/T一体，而无源则是分立的模块，即分开的模块。所谓相控阵指的就是通过不同T端的相位差产生的干涉波进行测距，这样就可以在不旋转天线的情况下进行几乎180°的测距(实际并不能达到)，而战斗机使用的相控阵雷达都是使用的电磁波，因为电磁波是光速。而我们没有办法做出这样的效果，所以我们使用超声波模块。

本期我们采用线性阵列天线，也就是下图所示，所有R/T均为蓝色三角形并在同一条直线上，方向固定。阵元(R/T模块)之间间距为d，目标在某一个角度$\theta$上那么我们可以计算：

5

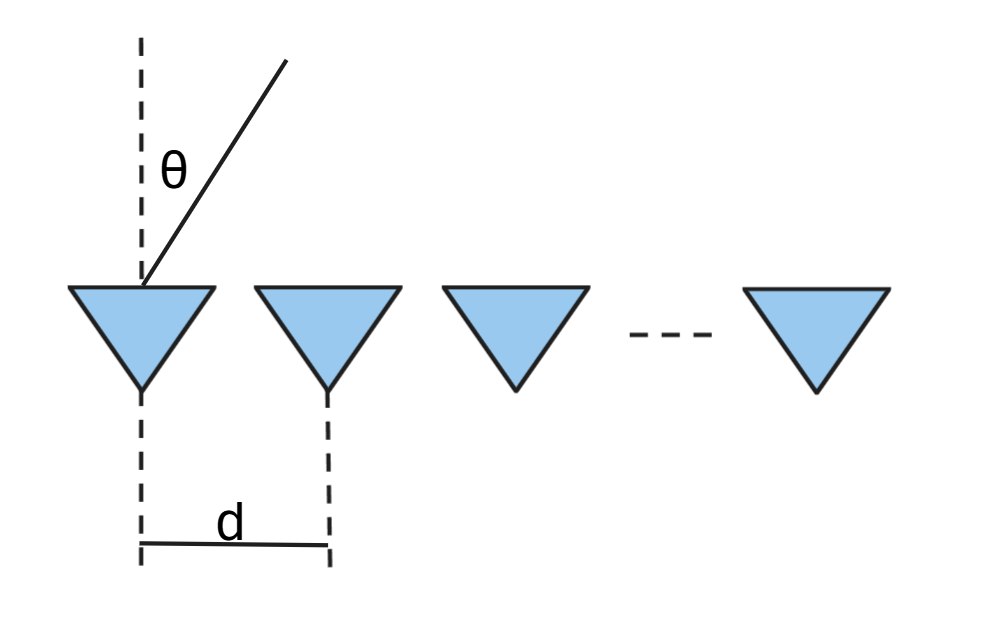
反弹相位差：

其中的$\lambda$为波长，相位差会引发路程差$\Delta L$。令：

然后我们需要确定相角度如何转化为数据发送时间延迟：

假设信号传播时间为$\Delta t$，则：

而这之中又包含下面的相角差异的公式。

所以我们需要完成的控制就是精确控制每个超声波模块发送声波的时间，以及采集回响时间。

  • 确定波束成形的角度$\theta$
  • 利用角度计算相位差
  • 计算模块时间延迟，每个模块都需要间隔一个时间延迟
  • 根据时间延迟发送波，并采集。
  • 采集回响信号时间(模块ECHO高电平时间)
  • 计算距离

仿真

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt

# 参数设置
num_elements = 8  # 阵列单元数目
element_spacing = 0.5  # 单元间距（以波长为单位）
scan_angle = 60  # 波束扫描角度（以度为单位）
phases = np.linspace(0, 2 * np.pi, num_elements)  # 每个单元的相角

# 创建方向余弦
theta = np.linspace(-np.pi / 2, np.pi / 2, 180)  # 扫描角度范围
psi = 2 * np.pi * element_spacing * np.sin(theta)  # 阵列因子

# 阵列因子计算
array_factor = np.zeros_like(theta, dtype=complex)
for n in range(num_elements):
    array_factor += np.exp(1j * (n * psi + phases[n]))

# 归一化阵列因子
array_factor = np.abs(array_factor) / num_elements

# 2D 绘图
plt.figure()
plt.polar(theta, array_factor)
plt.title('2D Array Factor')
plt.show()

# 3D 绘图
theta_grid, phi_grid = np.meshgrid(theta, theta)
X = np.sin(theta_grid) * np.cos(phi_grid)
Y = np.sin(theta_grid) * np.sin(phi_grid)
Z = array_factor * np.cos(theta_grid)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_title('3D Array Factor')
plt.show()

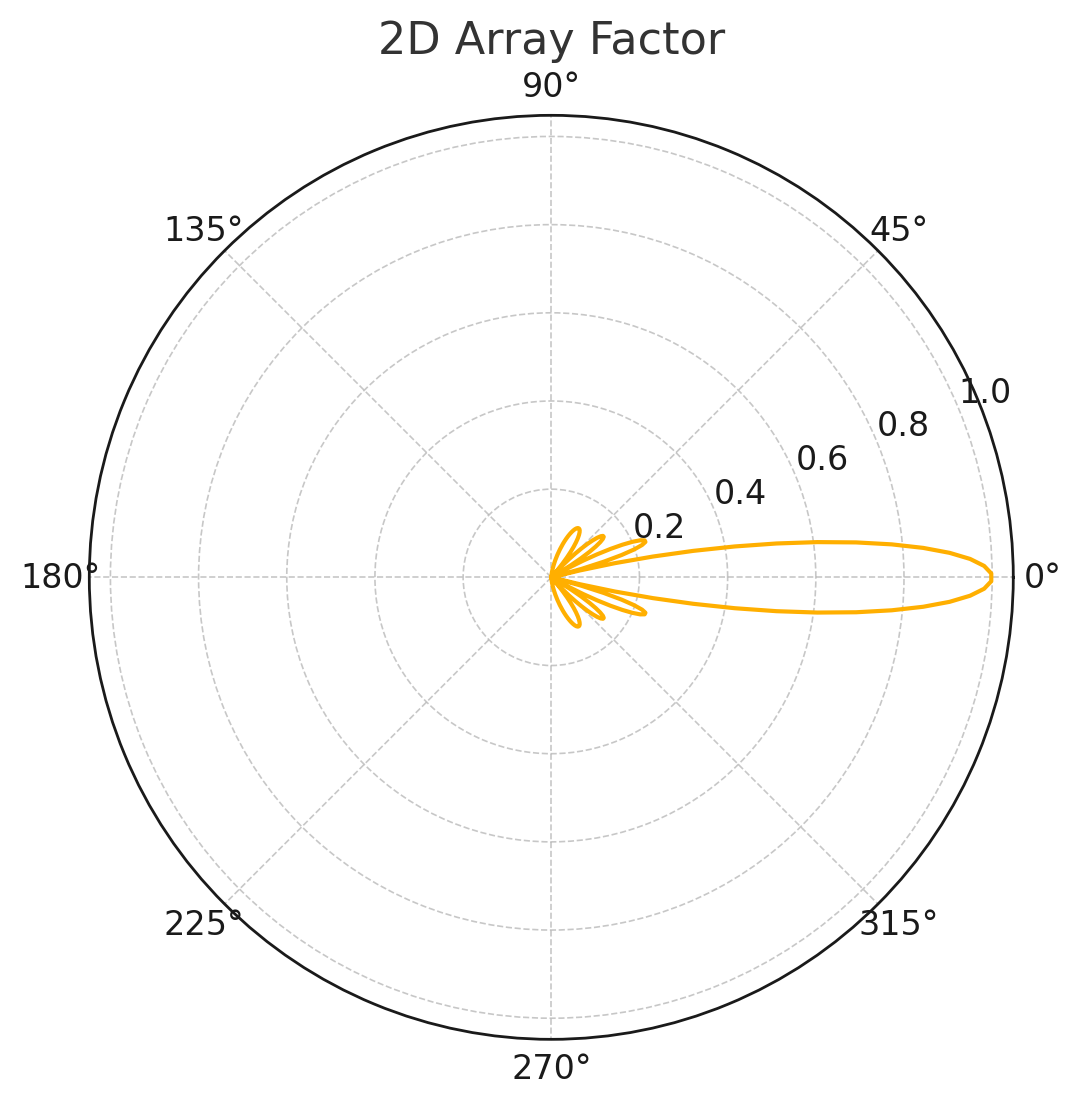
先试试0度下的阵列极坐标图：

1

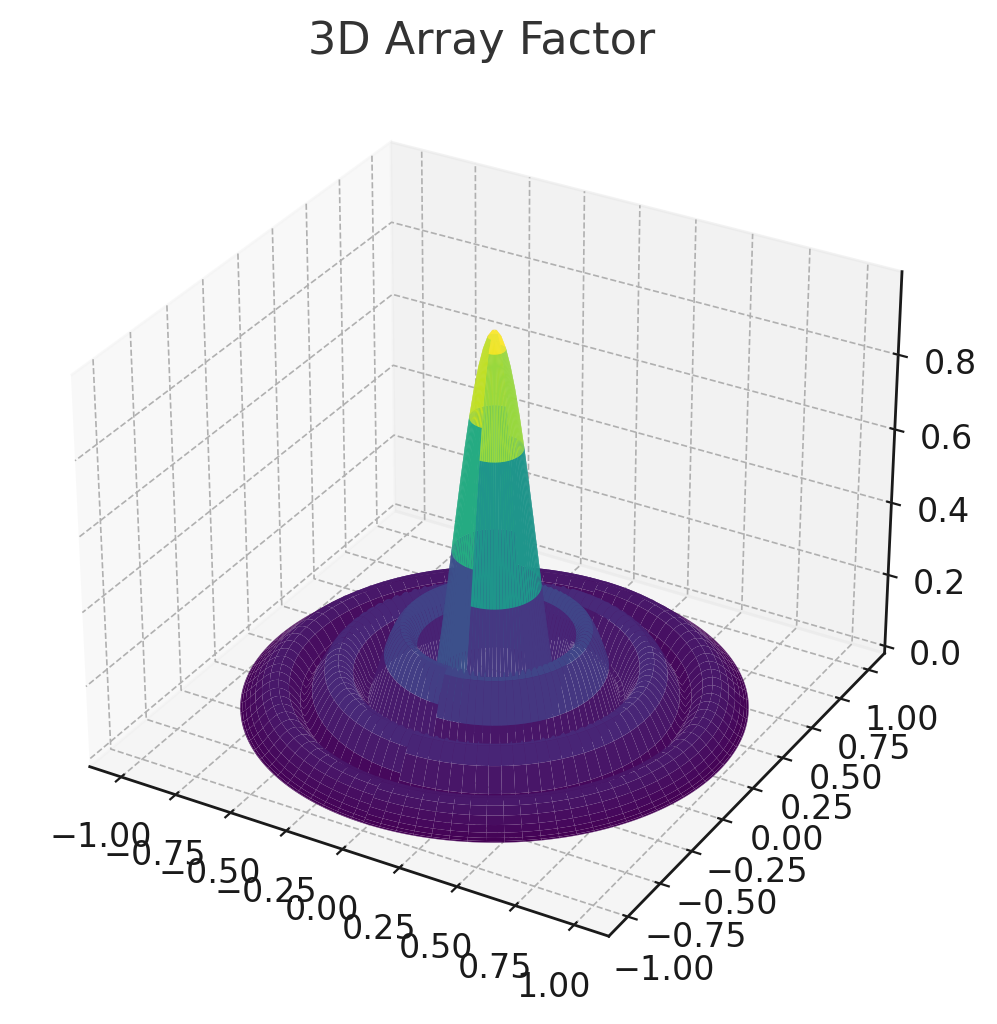
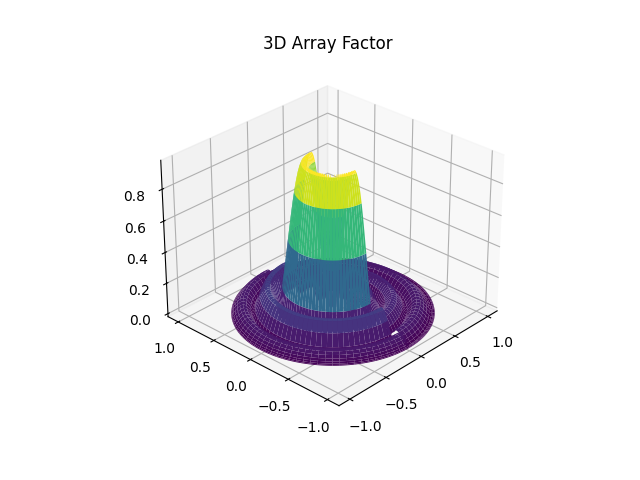
空间图为：

2

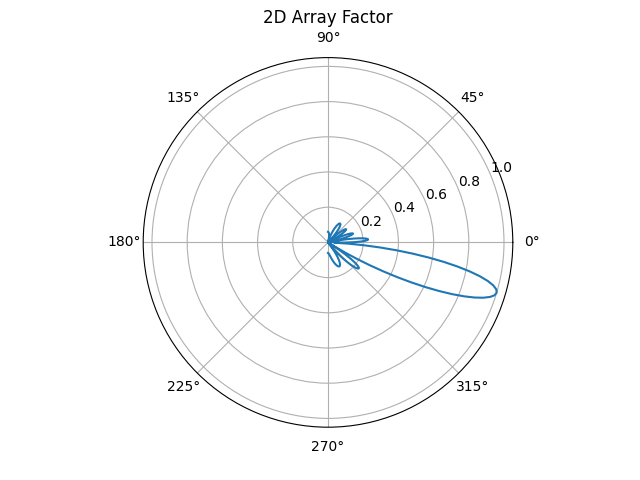
再试试60度：

3

4

实地部署

这里我使用了stm32f411ceu6，两个HC-SR04，这两个超声波模块的工作原理就是提供给Trig一段时间的高电平，然后就会触发超声波发送8个40KHZ的超声波，而echo会把信号传递时间化作高电平时间反映在echo引脚，也就是说echo引脚输出高电平时间就是信号传递时间。

首先我们需要一个us级的延时，这里我使用了定时器计数法，只要定时器给到1MHZ就可以实现每次1us计数一次了，这里我使用了tim2：

1
2
3
4
5
6
void delay_us(double us){
    HAL_TIM_Base_Start_IT(&htim2);
    __HAL_TIM_SET_COUNTER(&htim2, 0);
    while(__HAL_TIM_GET_COUNTER(&htim2) < us);
    HAL_TIM_Base_Stop_IT(&htim2);
}

再利用两个定时器分别采集超声波的echo信号时长。单位一样的1us。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
uint32_t P7_code = 0;
uint32_t P5_code = 0;

void HAL_GPIO_EXTI_Callback(uint16_t GPIO_Pin){
    // P5 or P7
    if(GPIO_Pin == GPIO_PIN_5){
        LED_OFF;
        if(HAL_GPIO_ReadPin(GPIOB, GPIO_PIN_5) == GPIO_PIN_SET){
            HAL_TIM_Base_Start_IT(&htim5);
        }
        else{
            HAL_TIM_Base_Stop_IT(&htim5);
            // 读取计数器的值
            P5_code = htim5.Instance->CNT;
            htim5.Instance->CNT = 0;
        }
    }
    else if(GPIO_Pin == GPIO_PIN_7){
        if(HAL_GPIO_ReadPin(GPIOB, GPIO_PIN_7) == GPIO_PIN_SET){
            HAL_TIM_Base_Start_IT(&htim3);
        }
        else{
            HAL_TIM_Base_Stop_IT(&htim3);
            // 读取计数器的值
            P7_code = htim3.Instance->CNT;
            htim3.Instance->CNT = 0;
        }
    }
}

其中的PB7和PB5是我的右和左的超声波模块，因为相控阵正前方才是0度，所以我们还需要区分正角度和负角度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void setPhase(double phase, Direction_E direction){
    if (phase < 1000){
        phase *= 1000;
    }
    if(direction == Forward){
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_6, GPIO_PIN_SET);
        delay_us(phase);
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_4, GPIO_PIN_SET);
        HAL_Delay(1);
        // 低电平
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_6, GPIO_PIN_RESET);
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_4, GPIO_PIN_RESET);
    }
    else if(direction == Backward){
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_4, GPIO_PIN_SET);
        delay_us(phase);
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_6, GPIO_PIN_SET);
        HAL_Delay(1);
        // 低电平
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_4, GPIO_PIN_RESET);
        HAL_GPIO_WritePin(GPIOB, GPIO_PIN_6, GPIO_PIN_RESET);
    }
}

在写一下中断回调函数和初始化就可以利用数据计算距离了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 定时器中断回调函数
void HAL_TIM_PeriodElapsedCallback(TIM_HandleTypeDef *htim){
    if (htim->Instance == TIM2) HAL_TIM_Base_Stop_IT(&htim2);

    if (htim->Instance == TIM3){
        HAL_TIM_Base_Stop_IT(&htim3);
        P7_code = 0;
    }
    if(htim->Instance == TIM5){
        HAL_TIM_Base_Stop_IT(&htim5);
        P5_code = 0;
    }
}


void AsynReadHR04Init(void){
    // 开启定时器中断
    HAL_TIM_Base_Start_IT(&htim2);
    HAL_TIM_Base_Start_IT(&htim3);
    HAL_TIM_Base_Start_IT(&htim5);
}

而计算方法很简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
double delta_t = 0;

void setDirection(int theta){
    // 相位差
    double Phi = 2 * PI * ElementSpacing * sin(theta * PI / 180) / Lambda;
    // 时间延迟
    double TimeDelay = Phi / (2 * PI * Frequency);
    // 发送波
    if(theta > 0)
        setPhase(TimeDelay, Forward);
    else
        setPhase(TimeDelay, Backward);
    // 位移差
    double delta_l = Phi * Lambda / (2 * PI);
    // 时差
    delta_t = delta_l / SoundSpeed;
}

double getDistance(){
    double time = P5_code * 0.0000001;
    return (time - delta_t) * SoundSpeed / 2;
}

这里的步骤就是上文说过的内容，接下来就是见证奇迹的时刻，我加入一个舵机反应角度

实验

6

7

技术
#C #ARM #相控阵雷达
超声波无源相控阵雷达
https://blog.minloha.cn/posts/1303139ce4927d2024090347.html
作者
Minloha
发布于
2024年9月3日
更新于
2024年9月16日
许可协议