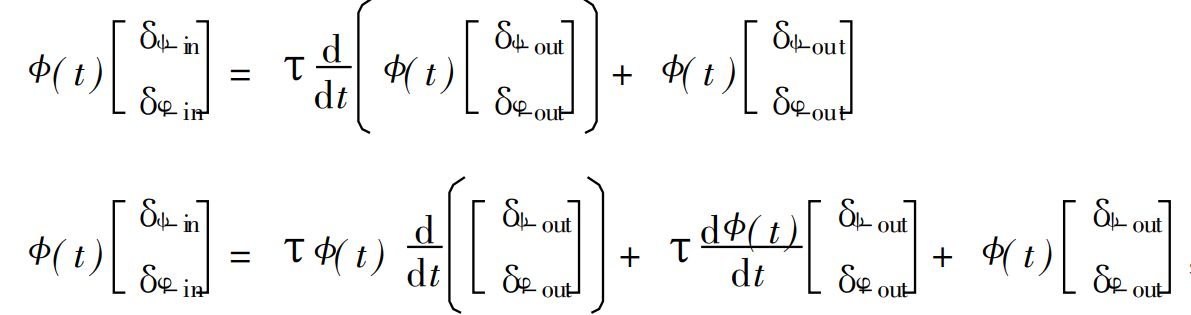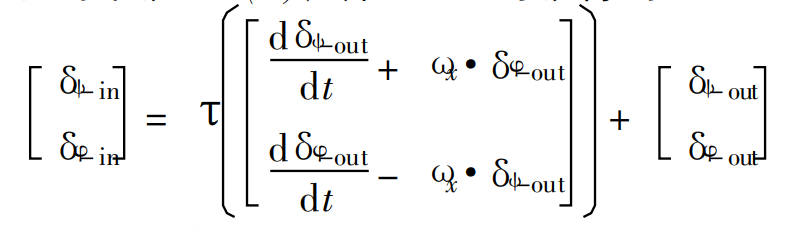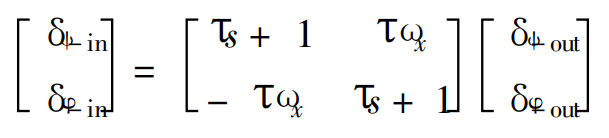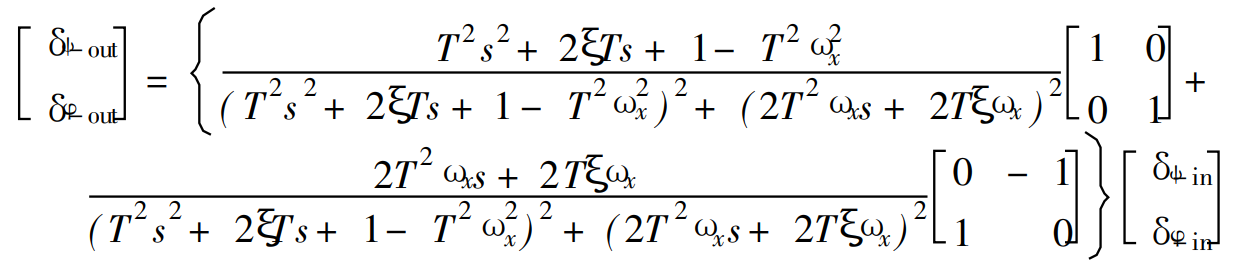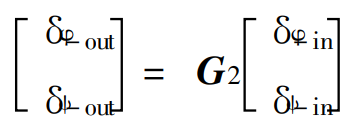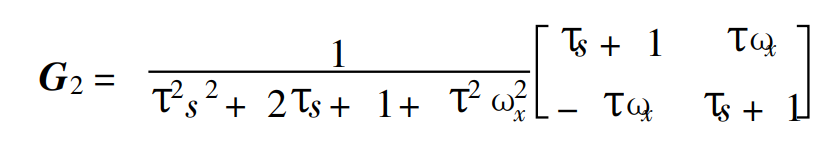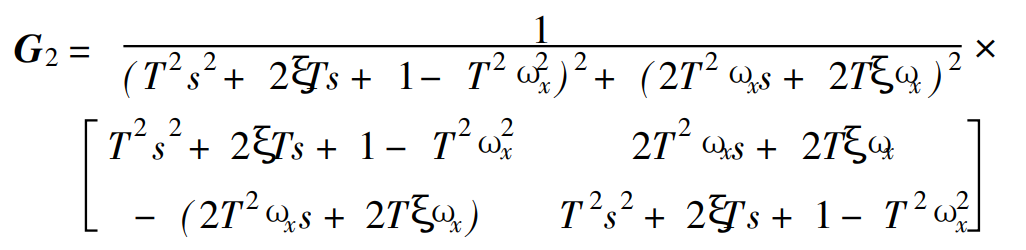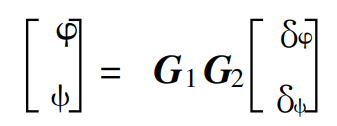火箭的控制原理——TVC与钱学森弹道

TVC姿态控制

假设我们的喷嘴是矢量喷口，则我们可以用$\delta_z$和$\delta_y$表达喷管的偏角。则$\delta_\phi$和$\delta_\omega$分别表达俯仰和偏航的等效角。对应的$\phi$和$\omega$对应俯仰角和偏航角，那么我们可以得到：

$$\delta_z=cos\omega_xt\delta_\phi+sin\omega_xt\delta_\omega$$ $$\delta_y=-sin\omega_xt\delta_\phi+cos\omega_xt\delta_\omega$$

而从等效角对应到具体角度可以用一个传递函数完成。

$$\phi=G_1\delta_\phi$$ $$\omega=G_1\delta_\omega$$

其中的G1可以是PID控制器。假设G1是积分系统。设输入信号为：

$$\delta_{\omega in}\delta_{\phi in}$$

和输出信号：

$$\delta_{\omega out}\delta_{\phi out}$$

则可以有：

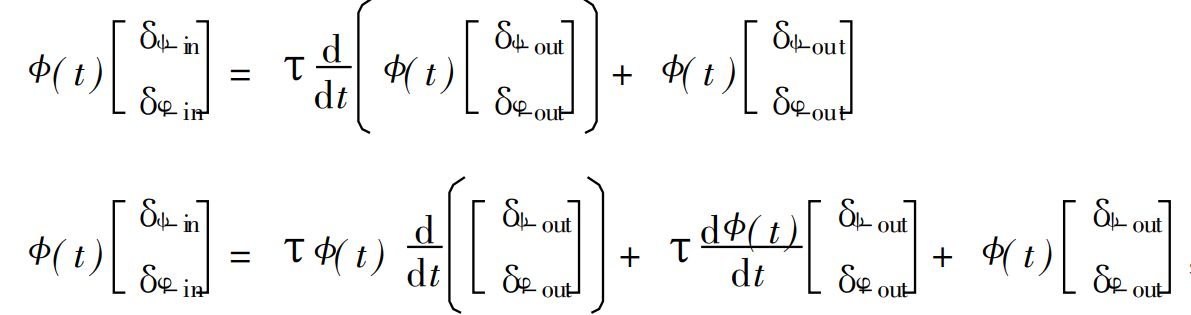
其中的$\phi(t)$为准坐标系到坐标系的转换矩阵。

两边同时取逆，可以得到：

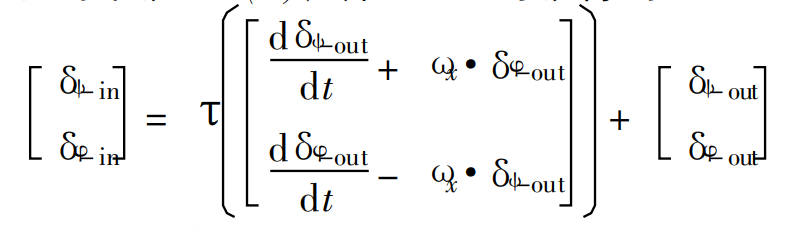
对两边进行拉普拉斯变换。

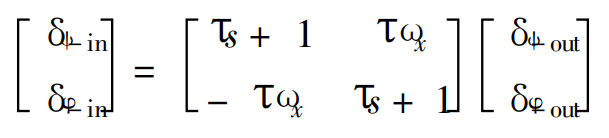
如果输入信号是二阶震荡信号可以有：

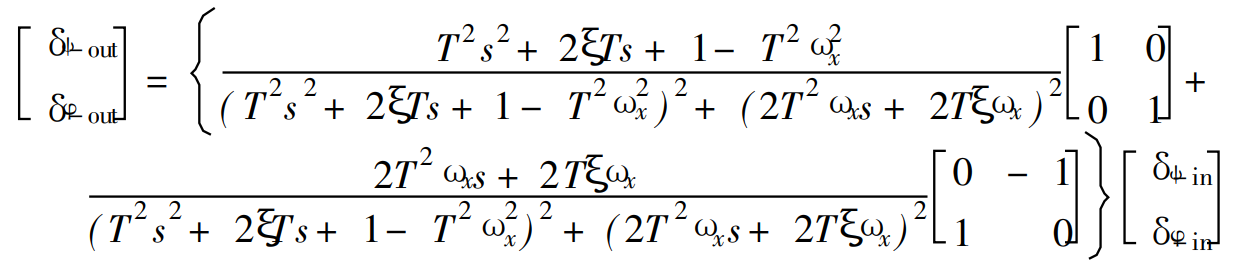
定义G2为延迟传递矩阵，可得：

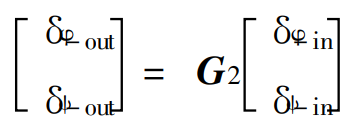
则一阶惯性伺服系统为：

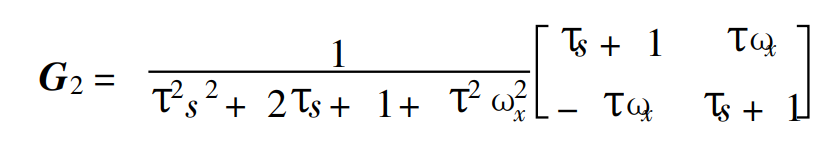
二阶惯性伺服系统：

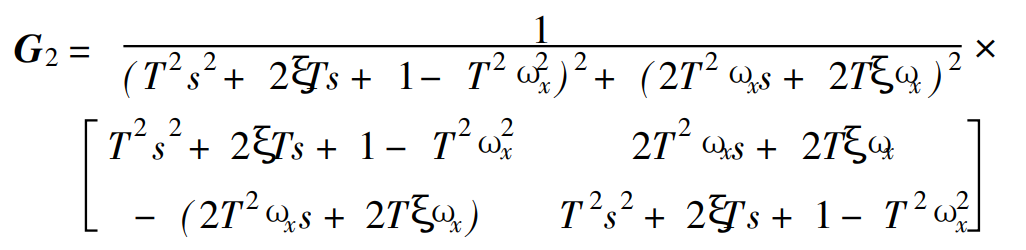
综上所述可以得到TVC开环传递公式：

---

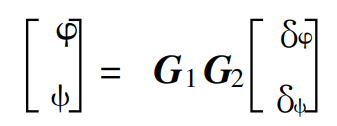
到目前为止我们已经清楚的了解到TVC控制的数学原理，为了可以精准控制姿态，我们需要对传递函数进行数学建模。接下来是具体控制器的运行过程。

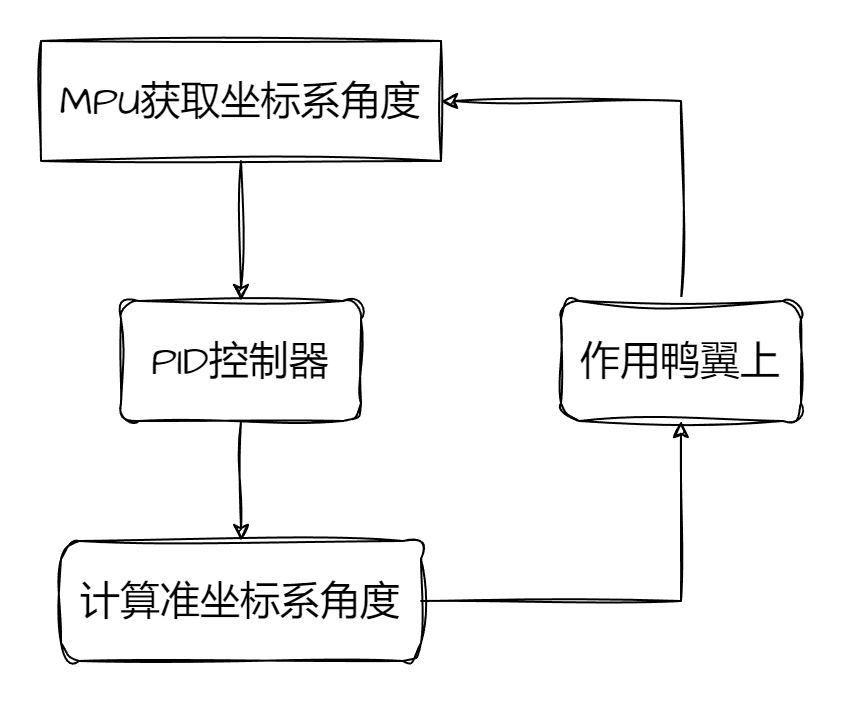
通过此算法可以保证推力矢量的稳定可控，接下来解释一下钱学森弹道

钱学森弹道

钱学森弹道是一个抛物线路径，曲线方程为：

$$y=ax^be^{-cx^d}$$

其中Y为纵向位移，X为横向位移，其中的abcd为常数，用于控制终点。

这个公式的用处不大，我们需要利用一些简单方法进行推导：

• 初速度：设导弹初速度为 $v_0$，发射角为 $ \theta_0$。
• 空气阻力：假设空气阻力$F_d$与速度v的平方成正比，即 $F_d = c_d v^2$，其中$c_d$为阻力系数。

• 运动分解：导弹的运动分为水平方向和竖直方向，分别考虑。

• 水平方向运动

水平方向上，假设不考虑空气阻力的情况，导弹的初始水平速度为 $v_{0x} = v_0 \cos\theta_0 $。

考虑空气阻力的情况下，水平速度的变化率可由以下方程表示：

$$\frac{dv_x}{dt} = - \frac{c_d}{m} v_x v$$

其中m为导弹质量，v是导弹瞬时速度 $v = \sqrt{v_x^2 + v_y^2}$。

由于空气阻力会减小水平速度，所以速度方程为：

$$v_x(t) = v_{0x} \cdot e^{-\frac{c_d}{m} t}$$

水平位移xt由速度积分得出：

$$x(t) = \int v_x(t) dt = \int v_{0x} \cdot e^{-\frac{c_d}{m} t} dt$$ $$x(t) = -\frac{m v_{0x}}{c_d} \cdot e^{-\frac{c_d}{m} t} + C$$

假设 t=0时x=0，则$C = \frac{m v_{0x}}{c_d}$，所以：

$$x(t) = \frac{m v_{0x}}{c_d} \left(1 - e^{-\frac{c_d}{m} t}\right)$$

• 竖直方向运动

竖直方向上，导弹初始速度为 $v_{0y} = v_0 \sin\theta_0$，受重力 mg 和空气阻力Fd的共同作用。

竖直速度的变化率为：

$$\frac{dv_y}{dt} = -g - \frac{c_d}{m} v_y v$$

同样的，通过解微分方程，可以得到竖直速度 $v_y(t)$ 和竖直位移 y(t)的表达式。由于过程较为复杂，我们给出解的形式：

$$v_y(t) = \left(v_{0y} + \frac{mg}{c_d}\right) \cdot e^{-\frac{c_d}{m} t} - \frac{mg}{c_d}$$

竖直位移 y(t) 为速度的积分：

$$y(t) = \int v_y(t) dt$$

同样假设 y(0) = 0，可以求得：

$$y(t) = \frac{m}{c_d} \left( v_{0y} + \frac{mg}{c_d} \right) \left(1 - e^{-\frac{c_d}{m} t}\right) - \frac{mg}{c_d} t$$

• 消除时间参数

为了得到导弹的轨迹方程 y(x)，我们需要消去时间 t。通过解水平方程 x(t) 得到 t 作为 x 的函数：

$$t(x) = -\frac{m}{c_d} \ln\left(1 - \frac{c_d x}{m v_{0x}}\right)$$

将其代入竖直位移方程 y(t)，即可得到y关于x的表达式：

$$y(x) = \frac{m}{c_d} \left( v_{0y} + \frac{mg}{c_d} \right) \left(1 - \left(1 - \frac{c_d x}{m v_{0x}}\right)\right) - \frac{mg}{c_d} \cdot t(x)$$

简化得到最终的轨迹方程：

$$y(x) = \left(v_{0y} + \frac{mg}{c_d}\right) \cdot \frac{x}{v_{0x}} - \frac{mg}{c_d} \cdot \frac{m}{c_d} \ln\left(1 - \frac{c_d x}{m v_{0x}}\right)$$

• 进一步简化（小空气阻力近似）

在空气阻力较小的情况下，即$ c_d \to 0$，轨迹方程可进一步简化为常见的抛物线形式：

$$y = x \tan(\theta_0) - \frac{g x^2}{2 v_0^2 \cos^2(\theta_0)}$$

对于有空气阻力确定落点的情况下：

初始速度 $v_0$ 和 发射角度 $\theta_0$ 已知,空气阻力 $F_d = c_d v^2$，其中 $c_d$ 是阻力系数，v 是速度。

2. 弹道方程

弹道方程的垂直和水平分量分别为：

$$\frac{dv_x}{dt} = - \frac{c_d}{m} v_x v$$ $$\frac{dv_y}{dt} = -g - \frac{c_d}{m} v_y v$$

其中，$v_x$和 $v_y$ 是速度的水平和垂直分量。

接下来用python代码完成路径仿真：

import numpy as np
import matplotlib.pyplot as plt

# 参数定义
g = 9.81  # 重力加速度 (m/s^2)
c_d = 0.005  # 阻力系数
m = 100  # 质量 (kg)
dt = 0.01  # 时间步长 (s)

# 定义不同的初速度 (m/s) 和发射角度 (度)
v0_values = [50, 70, 90]
theta_values = [30, 45, 60]

# 创建绘图
plt.figure(figsize=(10, 6))

# 绘制不同初速度和发射角度下的曲线
for v0 in v0_values:
    for theta0 in theta_values:
        # 将角度转换为弧度
        theta_rad = np.radians(theta0)

        # 初始条件
        v_x = v0 * np.cos(theta_rad)
        v_y = v0 * np.sin(theta_rad)
        x, y = 0, 0  # 初始位置

        # 用于存储轨迹的数组
        x_vals = []
        y_vals = []

        # 数值积分以确定弹道轨迹和落点
        while y >= 0:
            v = np.sqrt(v_x ** 2 + v_y ** 2)

            # 更新速度
            v_x -= (c_d / m) * v * v_x * dt
            v_y -= (g + (c_d / m) * v * v_y) * dt

            # 更新位置
            x += v_x * dt
            y += v_y * dt

            # 保存当前的 (x, y) 值
            x_vals.append(x)
            y_vals.append(y)

        # 绘制弹道轨迹
        plt.plot(x_vals, y_vals, label=f'v0 = {v0} m/s, θ = {theta0}°')

        # 标注落点位置
        plt.scatter(x, 0, color='red')
        plt.text(x, 0, f'({x:.1f}, 0)', fontsize=9, ha='right', color='red')

# 添加标题和标签
plt.title('ballistic trajectory')
plt.xlabel('distance (m)')
plt.ylabel('height (m)')
plt.legend()
plt.grid(True)

# 显示图形
plt.show()

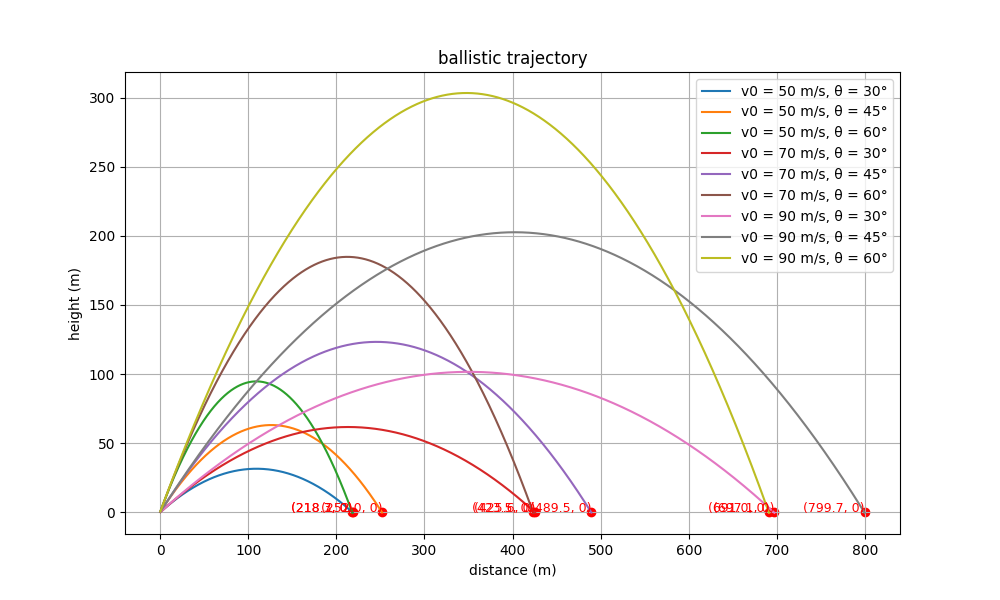
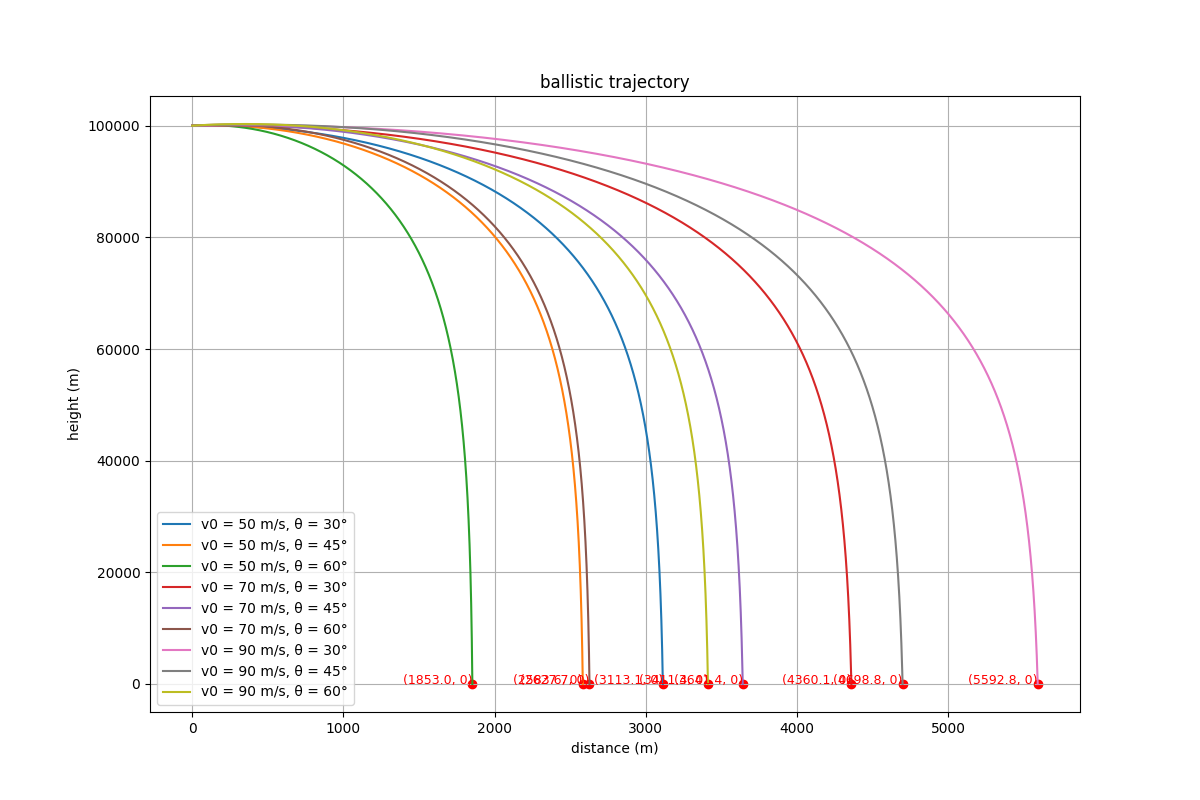
不要疑惑，钱学森弹道在突破大气层过程是图中的轨道，剩下的大气层打水漂过程我们无法完全仿真，因为需要考虑空气阻力，飞行器姿态控制，所以我们只能假设一下。

修改一下初始位置得到：

import numpy as np
import matplotlib.pyplot as plt

# 参数定义
g = 9.81  # 重力加速度 (m/s^2)
c_d = 0.005  # 阻力系数
m = 100  # 质量 (kg)
dt = 0.01  # 时间步长 (s)

# 定义不同的初速度 (m/s) 和发射角度 (度)
v0_values = [50, 70, 90]  # 初速度列表
theta_values = [30, 45, 60]  # 发射角度列表

# 创建绘图
plt.figure(figsize=(12, 8))

# 绘制不同初速度和发射角度下的轨迹
for v0 in v0_values:
    for theta0 in theta_values:
        # 将角度转换为弧度
        theta_rad = np.radians(theta0)

        # 初始条件
        v_x = v0 * np.cos(theta_rad)
        v_y = v0 * np.sin(theta_rad)
        x, y = 0, 100000  # 初始位置

        # 用于存储轨迹的数组
        x_vals = []
        y_vals = []

        # 数值积分以确定弹道轨迹和大气层内过程
        while y >= 0:
            v = np.sqrt(v_x ** 2 + v_y ** 2)

            # 更新速度
            v_x -= (c_d / m) * v * v_x * dt
            v_y -= (g + (c_d / m) * v * v_y) * dt

            # 更新位置
            x += v_x * dt
            y += v_y * dt

            # 保存当前的 (x, y) 值
            x_vals.append(x)
            y_vals.append(y)

        # 绘制弹道轨迹
        plt.plot(x_vals, y_vals, label=f'v0 = {v0} m/s, θ = {theta0}°')

        # 标注落点位置
        plt.scatter(x, 0, color='red')
        plt.text(x, 0, f'({x:.1f}, 0)', fontsize=9, ha='right', color='red')

# 添加标题和标签
plt.title('ballistic trajectory')
plt.xlabel('distance (m)')
plt.ylabel('height (m)')
plt.legend()
plt.grid(True)

# 显示图形
plt.show()