信息熵与赫夫曼算法

介绍

信息论

信息熵是信息论第一个研究的对象，在通信理论中，对于解决临界数据压缩的值和临界通信传输速率的值，对应就是信息熵和信道容量，而信道容量通常是由输入信号与输出信号的最大互信息决定。

赫夫曼算法不同于其他的编码，比如Shannon-Fano-Elias编码，它是一种基于最优树的码字算法，对于有限字符长度的信息，赫夫曼算法得到的编码具有更多的期望长度，不过两者平均编码长度一直在(H,H+1)内。

对于信息熵有计算公式：
$$
H(x)=-\sum_{x∈χ}^∞p(x)log_2, p(x)
$$

对于条件事件的信息熵，我们还可以通过两个随机变量写出联合熵，它的形式如下：
$$
H(X,Y)=-\sum_{x∈χ}\sum_{y∈Υ}p(x,y):log,p(x,y)
$$
简单的计算化简，还可以得到链式法则：
$$
H(X,Y)=H(X)+H(X|Y)
$$

χ是第二十二个希腊字母，读音类似英语单词He，读作/chi/

当然信息熵适用于基本事件概率不均等的信息熵求解，对数下是以2为底，所以H(x)的单位是bit，如果是ln p(x)得出的单位就是nat。显而易见的是，H(x)恒大于等于0，也就是熵的非负性。从概率p(x)我们可以推断出，x是一个泛函数，依赖于分布函数。

其他类型的编码比如信源编码和费诺编码本质原理相同，出于对图论的学习，我就不说了。

图论

对于树，我们可以区分为使用有向边连接的有向树和无向边连接的无树，对于一个有限的码字，假设它的长度为你，它可以自前向后分割为n个不同长度的子串，这些叫码字的前缀，而如果存在一个集合，它是一个有限长度码字前缀的集合，前缀之间不互相为前缀，那么叫集合内元素为前缀码，如果前缀码只使用了0和1表示，就说它是二元前缀码。

假设一个含权二元树，它保证每一条叶和枝所有权重最小，也就是满足下面表达式，其中L(w)表示结点所在层，求出的w(T)就是树权。
$$
w(T)=\sum_{i=1}^tw_iL(w_i)
$$
赫夫曼算法主要完成下面四个步骤：

• 1、将所有的结点含权放入集合C中
• 2、取出两个C中最小的元素，作为儿子，连接为父亲，父亲的权重为左儿子和右儿子的和
• 3、在C中去除两个儿子结点，加入父亲结点
• 4、判断C是否为空，不为空返回第二步

通过赫夫曼算法的到的根数就是最优树。从根开始依次给边赋权，左子树为1，右子树为0，那么就可以得出最优前缀码。

举例子

Minloha打算使用单片机通过传递电磁波完成选择题答案的传输，请你帮他设计一份编码，使数据传输最简洁。据统计，选择题出现A的概率为22%，出现B的概率为13%，出现C的概率为37%，出现D为28%

这题是单变量，那我们就用信息熵算出最大压缩量
$$
H(x)=-\sum p(x)log;p(x)
$$

$$
H(x)=-(0.22·log;0.22+0.13·log;0.13+0.37·log;0.37+0.28·log0.28)
$$

我们简单的计算一下，得到H(x)=1.90816694686取整为2，也就意味着我们只用2个码字就可以表示它们了，那我们画出它的二元树：

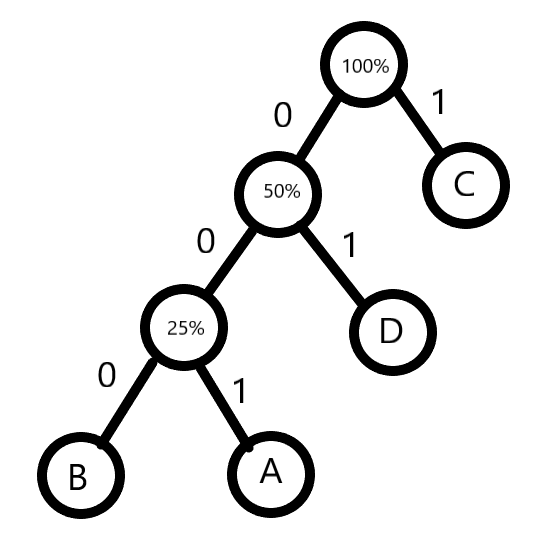
可以非常简单的看出，A表示为001，B表示为000，C表示为1，D表示为01，那么我们算一下平均码字长度，大小为2.25，比较接近我们的信息熵大小。

对比的，我们也算一下香农码，香农码计算公式为：
$$
l(x)=\lceil log;\frac{1}{p(x)} \rceil
$$
分别计算一下，可以算出A的码字长度为2.18442457114取整为3，B的码字长度为2.94341647163取整为3，C香农码字长为1.43440282415取整为2，D长1.83650126772取整为2，列表看看赫夫曼码字长度和香农码字长度大小比较

字符	理想码字长度	取整后码字长度	赫夫曼码字长度
A	2.18442457114	3	3
B	2.94341647163	3	3
C	1.43440282415	2	1
D	1.83650126772	2	2

可以看出赫夫曼编码还是十分契合理想码字长度的。

总结

本篇主要介绍了信息熵与赫夫曼编码的概念，通过阅读可以让读者明白计算的笔算方法，也可以通过不同的编程语言实现相应的功能。