浅谈图论

发展历史

在现在的计算机网络工程中，最不可或缺的就是拓扑图，其实拓扑图就是图的一个变种。对于拓扑学，它和图论的区别是应用场所不同，图是一个工具，而拓扑是切实通过代数运算的工具，拓扑应用的较多就是泛函分析，后面可能会说。图论在现代应用于线性代数或者密码学中，涉及表达的地方，都会有图存在。

图论是数学领域中发展最快的分支之一,数学史上著名的七桥问题欧拉只用了一步就证明了不重复地通过7座桥的路线是根本不存在的!这是拓扑学研究的先声。图的染色问题一直是图论研究的焦点问题。数学家赫伍德(Hedwood)成功地运用肯普的方法证明了五色定理,即一张地图能够用五种或者更少的颜色染色。美国伊利诺斯大学的黑肯(W.Haken)和阿佩尔(Appel),经过四年的艰苦工作.终于完成了四色猜想的证明。正是上述那些似乎没有多大意义的游戏的抽象与论证的方法,开创了图论科学的研究。

图

这就是图

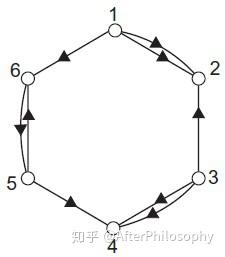
点和边

图论的要素就是点和边了，点没什么说的，用一个空心圆表示点。边有区别，在离散数学的二元关系的一章中，会知道二元关系就是图论中的一种叫有向边的边，在图上表现出序偶的第一元素用箭头指向第二元素。写出来一个从a到b的二元关系为<a,b>。如果描述的是集合之间的二元关系如A和B，那么就可以写为笛卡尔积A×B表示A与B之间的二元关系。相似的，对于A到B集合也可以从函数角度分析，A集合通过映射f到B集合，为了映射达到满射，引出了函数的置换，记作：

其中n叫做置换阶，常见的比如切比雪夫多项式，就是一种置换函数。有向边组成的有向图的一个性质是度(degree)，对于一个点它可以有出度和入度，表示为deg(v)，它可以衡量图的同构。相似复习一下二元关系在有向图的性质，也就是下面的三个性质。

  • 自反性(r)
  • 对称性(s)
  • 传递性(t)

在初学二元关系就已经引入图了，所以有向图应该是接触较早的。在学习二元关系中有一个难点，就是等价关系和次序关系，等价关系是一个同时具备自反性，对称性和传递性的关系R，在他的元素集合A中，满足：

同时对于关系R，它的第一元素组成的集合是集合A的等价类。次序关系中比较难的就是偏序关系，拟序关系还好说，拟序集用符号<A,<>表示，偏序集用符号<A,≤>表示。对于偏序关系R，他要有自反性，反对称性和传递性。这里会引出哈斯图的概念，不过无非就是省略自环和箭头的图，也就不细说了。同时对偏序关系的特殊元素还要记得，最大与极大、最小与极小，不一定同时存在。

如果两元素不存在向性关系，也就是无序，那就可以用无序对表示，同样，对于元素a、b它的无序对表示为(a,b)。也可以用集合的笛卡尔积表示，不复写了。一般对于一个图(Graph)点一般放进集合V，边放进集合E，则对于一个图可以记作G=<V,E>，可以画图或者使用邻接矩阵表示，对与矩阵也就会有类似矩阵方程的计算，离散中独有的就是布尔乘积，它是通过类似矩阵乘法的叉乘，不过最终点是通过析取联结词运算的。

源自知乎

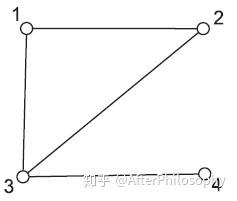
图的性质

对于有向图，一个节点v，他有n个以它为第二元素的序偶，则它的入度为n，记作$deg^-(v)=n$反之有m个以它为第一元素的序偶，则它的出度为m，记作$deg^+(v)=m$，对于整个图中，最大度记作Δ，最小度记作δ，最大最小出入度就是分别在右上角标号。而握手定理描述的就是下面的式子：

含义就是所有度数加和应为边数的二倍。

对于无向图，对其任意两个结点存在一条边能相互直达，就说两点是连通的，通常用连通性矩阵P表示。如果连通性矩阵的每一个元素都是1，那么图叫做连通图，反之叫做非连通图。自然的，图的等价类所有的导出子图都被称作为连通分支。而对于连通度，如果图G满足：

则V’’叫做点割集，如果|V’’|=1则叫做割点。同理如果图G满足：

则E’’叫做边割集，如果|E’’|=1叫做桥。而根据割集元素数量和种类，就引出了连通度的概念，即k(G)=min{|V’’| | V’’是点割集}，结果就是连通度k，V’’是点，则叫j做k-连通图，反之k(G)=min{|E’’| | E’’是边割集}，结果是连通度k，叫做k边-连通图。假设一个图，如果去掉所有有向边是连通的，就说图是弱连通，如果存在一对结点时连通的，就说时单向连通，如果任意节点均可达，就说是强连通的。假设等价关系的导出子图具有连通性，并且是有强弱之分，那么就可以分别命名为强连通分支，弱连通分支和单向连通分支。

对于边是含权的，如果需要计算任意两节点间的路径长度和最短路径，就需要下面两个算法

算法

dijkstra算法

如果你有学习过算法，你一定对他不陌生，他是通过不断转移标号，获取经过所有结点的一种算法，出于理解，我会用C++完成这个算法。dijkstra算法的思路是，从根节点开始标记为不定标签U，其余所有结点标记为变化节点V，寻找从U至V的最短路径，找到之后将最短的标记为U，重复上述步骤，直到被标记的是终点结点即可。

  • 第一步，标记根结点为U，找出与之相邻的结点路径，在距离表中保存它们的距离
  • 第二步，在相邻结点中找出距离下一组不包含V标记的结点中路径最短的，利用V标记当前结点，计算当前结点到下一组的所有距离，保存进距离表
  • 第三步，在未标记结点中继续寻找最短的，然后重复步骤二，直到所有点被标记完
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
//========================
// Dijkstra算法
// Author      : Villalba Caceres Vicente Javier
// Translate   : Minloha
// Name        : Dijkstra
//========================
#include <iostream>;
#include <queue>;
#include <vector>;

using namespace std;

struct Edge{
	int node;
	int cost;
	Edge(int _node, int _cost) : node(_node), cost(_cost) {}
	Edge() : node(-1), cost(-1) {}
};

struct Graph{
	vector<Edge> G[100];
	int V = 1;
	int E = 1;
};

struct State{
	int node;
	int cost;
	State(int _node, int _cost) : node(_node), cost(_cost) {}
	bool operator <(const State& b) const{
		return cost > b.cost;
	}
};

int algoritmo(const int begin, const int end, const Graph graph){
	priority_queue<State> pq;
	vector<int> Dist(graph.V, 0x3f3f3f3f);
	vector<bool> mark(graph.V, false);

	Dist[begin] = 0;
	pq.push(State(begin, 0));
	while (!pq.empty()){
		State st = pq.top(); pq.pop();
		mark[st.node] = true;
		if (st.node == end)
			return st.cost;

		int T = (int)graph.G[st.node].size();
		for (int i = 0; i < T; ++i){
			if (!mark[graph.G[st.node][i].node] && ((Dist[st.node] + graph.G[st.node][i].cost) < Dist[graph.G[st.node][i].node]))
			{
				Dist[graph.G[st.node][i].node] = st.cost + graph.G[st.node][i].cost;
				pq.push(State(graph.G[st.node][i].node, st.cost + graph.G[st.node][i].cost));
			}
		}
	}
	return -1;
}

struct Programa{
	int V, E;
	int comienzo, fin;
	void definirGrafo(Graph& graph){
		cout << "输入点数：" << endl;
		cin >> V;
		cout << "输入边数：" << endl;
		cin >> E;

		graph.V = V;
		graph.E = E;
	}
	void cargarGrafo(Graph& graph){
		for (int i = 0; i < E; ++i){
			int Origen, Destino, Peso;
			cout << "边" << i <<"的第一元素:" << endl;
			cin >> Origen;
			cout << "边" << i << "的第二元素: " << endl;
			cin >> Destino;
			cout << "边" << i << "输入边的权重:" << endl;
			cin >> Peso;

			graph.G[Origen].push_back(Edge(Destino, Peso));
			graph.G[Destino].push_back(Edge(Origen, Peso));
		}
	}
	void Dijkstra(Graph graph){
		cout << "输入根结点: " << endl;
		cin >> comienzo;
		cout << "输入终点:" << endl;
		cin >> fin;
		int n = algoritmo(comienzo, fin, graph);
		cout << "Dijkstra计算的距离: " << n << endl;
	}
};

int main(){
	bool out = false;
	char salir;

	Programa programa;
	Graph graph;

	while (!out){
		programa.definirGrafo(graph);
		programa.cargarGrafo(graph);
		programa.Dijkstra(graph);

		cout << "离开?(Y/N)" << endl;
		cin >> salir;
		if (salir == 'Y' || salir == 'y') {
			out = true;
		}
	}
}

你可以用此算法完成自己的图与Dijkstra距离。

Fluyd算法

这个算法的C++版本我短时间写不出来，那就只能说流程了呀~

  • i=0，首先规定自环距离为0，然后列举所有结点的距离，不可一步到达在矩阵中记作∞
  • i++，保留上一步矩阵中i行i列元素和主对角线元素，将其他位置的元素与保留下来的i行i列元素加和，如果和小于原有的值，则替换，得到新矩阵（如此循环）
  • 当i达到结点个数时，停止计算，则对应行列就是最短距离

相关的公式如下：

规定d为D的某行某列元素，则满足：

而d的计算满足：

而如果手算Floyd就十分有趣了，表示出图的加权邻接矩阵，通过保留主对角线上行列元素已经对应行与列，迭代到所有点之后，就能算出不同起点到不同终点的路径了。

dijkstra代码源自https://github.com/jpieroabarcam/Dijkstra.git，仅仅去掉注释和汉化一下

笔记
#C++ #离散数学 #算法
浅谈图论
https://blog.minloha.cn/posts/140429bf5fce562022040403.html
作者
Minloha
发布于
2022年4月4日
更新于
2024年9月15日
许可协议