离散数学基础
[一]集合论
集合论是非常简单又基础的,在高中数学的第一章便是集合论,因为内容重复,我只说简单的提一句。
集合要有以下性质:
- 互斥性:集合内没有重复的元素
- 无序性:集合内元素没有先后顺序
- 确定性:元素一定可以被确定是或否属于集合
集合的关系与运算
集合之间主要有子集和真子集的父子关系,或者等集表示两个互为子集的集合,一般记作集合A=集合B即:A=B。集合的表达常用的有三种,描述法,列举法,Venn氏图法,描述法就是对集合内的元素的区间加以描述,比如:
- A={ 所有的地球人 }
列举法就是列举出集合内所有元素,比如:
- B={ Minloha,Minloha的女朋友 }
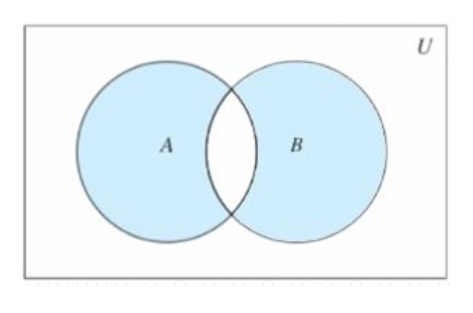
Venn氏图法可以通过直观的图形描述,这里就不举例了。
集合的运算
集合运算是简单的,同样的,集合运算也适用于概率论中事件的运算。集合运算有以下几种
- 交集:取出集合的公共部分,组成新的集合$A∩B$
- 并集:将集合所有元素构成一个新的集合,新集合要满足集合的性质记作$A∪B$
- 补集:从一个集合中取出当前集合不具有的元素,组成新的集合,记作$\bar A$或者$C^A_U$意味在全集U中的补集
- 差集:从一个集合中拿出另一个集合的部分,记作$A-B$,公式可以写作$A∩\bar B$意味A与B补集的交集

- 对称差集:指集合交集在并集中的补集,记作$A⊕B$,表示的集合是$(A-B)∪(B-A)$
这里主要有几个常用的公式:
- 分配律
- $A∩(B∪C)=(A∩B)∪(A∩C)$
- $A∪(B∩C)=(A∪B)∩(A∪C)$
- 吸收律
- $A∩(A∪B)=A,A∪(A∩B)=A$
- 德摩根律(记得变号)
- $ \overline{(A∪B)} = \bar A∩\bar B$
这些定律都可以通过Venn图表示证明,都是非常简单的。
集合的限度
集合可以分为有限集和无限集,而无限集又分为可数集合和不可数集合两类,我们把映射的含义拿来定义可数集合,规定自然数集N,如果集合与N存在对应关系Ψ使得集合与N之间每一个元素都存在一一对应关系,那么就说这个集合是可数的。而这个运算关系,也可以理解为是在计算集合的势能,所以也可以说是集合与自然数集N等势。等势集合一般记作下面的形式:
很像映射,也确实是一种映射关系。
如果集合A与自然数集N等势,那A是可数集合,记作$Χ_0$读作阿列夫零。同时有理数集合是可以用自然数的除法表示所有元素的,所以有理数集也是可数集合。而不可数集合就是与$(0,1)$开区间等势的集合,记作$Χ$。
而判断集合是否是可数的集合,只要找出对应的关系Ψ就可以了,
集合的应用
集合用于描述解决方案以及列举描述元素,它主要应用于概率论中,在离散数学我们几乎只涉及其表示方法,下面是一个例题,可以参考一下
传说在20人中,一定有10人是会编程的,10人会唱歌的,6人既会编程又会唱歌,问既不会编程又不会唱歌有几人
可以设所有人为全集U,会编程的人组成集合A,会唱歌的组成集合B,可以写出$A∪B$,就是所有会编程和会唱歌无重复元素的集合,那么他的补集就是待证的集合,$\overline{A∪B}= |A| + |B| - |A∩B|=10+10-6=14$,那么补集大小就是20-14=6,所以会有6人不会编程,不会唱歌。
[二]计数原理
这里在高中教材中同样有,这里的难点不是在计算,而是在思考解决问题的算式。同时在描述一些复杂的流程或者是在学习概率论的分布时,都会接触计数原理的内容。
计数原理在离散数学中主要介绍两个计算原理和两种数(排列组合),如果感兴趣可以在文末的评论区留言,我可能会出一期排列组合的博客,讲一讲常用的排列组合模型!对高考生也是有帮助的哟~
乘法与加法原理
乘法原理主要讲的是如果一件事情需要分成若干步,每一步都有不同数目的选择,那么最终可以产生的方案就是不同步骤下选择的乘积。即$n_1×n_2×n_3×n_{….}$,举例说:Minloha要从北京到上海,再去深圳。假设北京到上海有7种交通工具可以选择,上海到深圳有8种交通工具可以选择,那么Minloha可以有几种方案到达深圳?
很简单,7×8=56就可以了,这就是乘法原理的应用
加法原理主要讲的是情况,比如处理一件事有AB两种情况,那么只需要把不同情况下的选择数加和就可以了,也可以写作为$i_1+i_2+i_3+i_{…}$,举例说:Minloha已经到达了深圳,现在Minloha要去买一台电脑,A电脑店有20台电脑,B电脑店有10台电脑,请问Minloha有多少种选择?
答案很简单,就是20+10=30,也就是把具体的情况加和
排列组合
排列组合主要是他的含义,排列数在高中教材被写为$A_n^m$表示从n开始向减小的方向乘以m个数字,概率意义是从n个元素中有顺序的抽取m个。计算可以看例子,比如$A_4^2$表示从4开始向后乘两位,即4×3=12,而在《离散数学及其应用第三版》中将他写作为$P_n^m$,表达的含义是一样的。对于排列的计算可以有公式:
而组合数同样的记作为$C_n^m$表示从n个元素无顺序的取出m个,计算可以写作以下格式:
应用
应用主要讲两个原理,对于高中学过排列组合的一定都背过那些模型,插空隔板什么的。
对于常用的排列组合模型,我就不细说,直接一道题看看
将标号为1、2、3、4、5、6的张卡片放入三个不同的信箱中,如果每个信箱放两张,其中标号1、2放入一个信箱中,则不同的分发有几种?
解析:因为1、2已经确定,则只要分3、4、5、6就可以了,则有$C_4^2C_2^2$种针对余下的新的分发,而三个信箱所放信件各不相同,所以总体结果要乘以3。
答案是:$3×C_4^2C_2^2$=18种
容斥原理
所谓容斥原理,说的其实很简单,就是人们排斥不想要的,包容想要的,但有些问题比较特殊,需要包含错误内容作为补偿,这个原理就叫容斥原理,在高中数学中主要体现在计算模型:总体剔除,定序缩倍。
抽屉原理
这是一个在小学学习的内容,简单的说,你有5个苹果,要放进4个抽屉中,在保证每个抽屉都有苹果的前提下,必然有一个抽屉里面有两个苹果,这就是抽屉原理。
最后简单的来一个排列组合问题,高中难度的哟!
公司安排5位员工前往3个地点出差,要求每个人都要去,每个人只要去一个地方,请问有几种方案?
答案是:$A_5^3$=60种方案