强化学习网络与机器人控制——探索学习

RainBow

首先给出论文的地址：

https://arxiv.org/abs/1710.02298

这篇论文给出了一种融合度很高的深度强化学习模型，在其介绍部分详细说明了双DQN或者分布式Q学习的研究情况，也介绍了噪声DQN使用了随机网络（RND）进行了探索，但是都可以发现Q表格学习各有特色，归纳其中的特色就得到了RainBow模型（像彩虹一样花里胡哨）

正如作者所说，尽管DQN可以解决具有较高维度观测空间的问题，但是它只能处理离散且低维度的动作空间。并且由于DQN依赖动作价值函数的最大化，所以在连续空间下都需要进行离散后迭代优化，所以它无法直接应用在连续的状态空间。

所以为了解决一些问题，作者提出了一种离轨策略的AC方法，并且融合了很多内容，首先它学到了优先级经验回放，优先回放对学习更有帮助的经验（例如 TD 误差较大的经验），从而加速学习过程。而这对比DQN与DDQN的等概率采样有更强的优势。

其次RainBow是多步TD，可以传播更多的奖励。同时Rainbow也是离轨策略，通过目标网络进行动作选取，可以避免离散的动作空间对网络产生的稀疏奖励问题。通过分析对比RainBow的学习特点，它与DQN这种学习期望Q值的方法不同，它包含了近端优势（Advantage），可以非常方便的表达Q，特别是对那些对结果影响甚微的动作。

最后也是Rainbow真正的亮眼点就是它采用噪声网络代替了$\epsilon$贪心，贪心不可控而噪声网络是可学习的，网络可以根据情况调整自己的好奇心从而进行有效的学习。

首先介绍一下经验池，这个方法是强化学习非常基础的概念，类似与SARSA，它通过记录每一次转移情况进行保存，学习经验从经验池中采样，他的优化方法如下：

$$(R_{t+1}+\gamma_{t+1}\max q_{\theta}(S_{t+1},a')-q_\theta(S_t,A_t))^2$$

这个方法看着很眼熟，其实就是SARSA方法的一步更新，而更新的参数$\theta$代表了网络参数，这个方法可以通过RMSprop进行学习（小批量学习）

1、双Q网络

其次就是DQN的一些扩展方法，其中首当其冲的就是DDQN（双重Q学习），传统的Q学习受限于最大化Q值带来的误差而损害学习效果（因为DQN学习的并未Q的分布函数，而是Q的均值），所以D-DQN提出了一种新的更新方法如下：

$$(R_{t+1}+\gamma_{t+1} q_\theta^- (S_{t+1},arg\max_{a'}q_{\theta} (S_{t+1},a'))-q_\theta(S_t,A_t))^2$$

这种方法被证明可以减少DQN存在的均值与实际高偏差的现象。

2、优先经验回放

DQN从保存了一些组的经验缓冲区进行均匀采样（等概率），而在理想状态下我们希望可以学到更多有用的状态转换，所以提出了一种优先经验回访的方法，它是一种根据TD误差以p概率的转换（提供优先的就是这个概率p）

$$p_t\propto |R_{t+1}+\gamma_{t+1}\max_{a'}q_{\theta}^-(S_{t+1,a'})-q_{\theta}(S_t,A_t)|^\omega$$

3、类似AC网络

RainBow实现了类似AC网络的结构，采用了价值网络和优势网络，他们共享同一个卷积层，并利用下面的公式进行聚合。

$$q_\theta(s,a)=v_{\eta}(f_{\xi}(s))+a_{\psi}(f_{\xi}(s),a)-\frac{\sum_{a'}a_{\psi}(f_{\xi}(s),a')}{N_{actions}}$$

4、噪声网络

这也是Rainbow的特色所在，他抛弃了Linear层而是噪声层，参数传播给定了噪声参数：

$$y=(b+Wx)+(b_{noisy}·\epsilon^b+(W_{noisy}·\epsilon^\omega)x)$$

通过上述的所有内容进行组合，就得到了RainBow模型，这里我参考了一部分Github的开源代码，进行了适当的缩减，下面是噪声网络的实现：

# 噪声层
class NoisyLinear(nn.Module):
    def __init__(self, in_features, out_features, std_init=0.4):
        super(NoisyLinear, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.std_init = std_init
        self.weight_mu = nn.Parameter(torch.Tensor(out_features, in_features))
        self.weight_sigma = nn.Parameter(torch.Tensor(out_features, in_features))
        self.bias_mu = nn.Parameter(torch.Tensor(out_features))
        self.bias_sigma = nn.Parameter(torch.Tensor(out_features))
        self.reset_parameters()

    # 重置参数
    def reset_parameters(self):
        mu_range = 1 / np.sqrt(self.in_features)
        self.weight_mu.data.uniform_(-mu_range, mu_range)
        self.weight_sigma.data.fill_(self.std_init / np.sqrt(self.in_features))
        self.bias_mu.data.uniform_(-mu_range, mu_range)
        self.bias_sigma.data.fill_(self.std_init / np.sqrt(self.out_features))

    # 前向传播
    def forward(self, x):
        weight_epsilon = torch.randn_like(self.weight_sigma)
        bias_epsilon = torch.randn_like(self.bias_sigma)
        weight = self.weight_mu + self.weight_sigma * weight_epsilon
        bias = self.bias_mu + self.bias_sigma * bias_epsilon
        return F.linear(x, weight, bias)

然后实现个Dueling DQN（也就是模型改动的本体）

# Dueling Network
class DuelingNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, atoms=51):
        super(DuelingNetwork, self).__init__()
        self.action_dim = action_dim
        self.atoms = atoms
        self.feature_layer = nn.Sequential(
            nn.Linear(state_dim, 128),
            nn.ReLU(),
            nn.Linear(128, 128),
            nn.ReLU()
        )
        self.value_stream = nn.Sequential(
            NoisyLinear(128, 128),
            nn.ReLU(),
            NoisyLinear(128, atoms)
        )
        self.advantage_stream = nn.Sequential(
            NoisyLinear(128, 128),
            nn.ReLU(),
            NoisyLinear(128, action_dim * atoms)
        )

    def forward(self, x):
        features = self.feature_layer(x)
        value = self.value_stream(features).view(-1, 1, self.atoms)
        advantage = self.advantage_stream(features).view(-1, self.action_dim, self.atoms)
        q_dist = value + advantage - advantage.mean(1, keepdim=True)
        return F.softmax(q_dist, dim=-1)

经验池的实现也很简单，我们初步并不需要进行复杂的采样，我们先实现一个容器：

# Replay Buffer
class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = deque(maxlen=capacity)

    def push(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):
        return random.sample(self.buffer, batch_size)

    def __len__(self):
        return len(self.buffer)

最后实现整个智能体：

class RainbowAgent:
    def __init__(self, state_dim, action_dim):
        # 初始化 RainbowAgent 类
        self.state_dim = state_dim  # 状态空间的维度
        self.action_dim = action_dim  # 动作空间的维度
        self.atoms = 51  # 用于 Distributional RL 的原子数量
        self.v_min = 0  # Q 值分布的最小值
        self.v_max = 200  # Q 值分布的最大值
        self.support = torch.linspace(self.v_min, self.v_max, self.atoms).to(device)  # 生成均匀分布的支撑点
        self.delta_z = (self.v_max - self.v_min) / (self.atoms - 1)  # 支撑点之间的间隔

        # 初始化策略网络和目标网络
        self.policy_net = DuelingNetwork(state_dim, action_dim).to(device)  # 策略网络（用于选择动作）
        self.target_net = DuelingNetwork(state_dim, action_dim).to(device)  # 目标网络（用于计算目标 Q 值）
        self.target_net.load_state_dict(self.policy_net.state_dict())  # 同步目标网络和策略网络的权重
        self.optimizer = optim.Adam(self.policy_net.parameters(), lr=0.0001)  # 优化器

        self.memory = ReplayBuffer(10000)  # 经验回放缓冲区

    def act(self, state, epsilon=0.1):
        # 根据当前状态选择动作
        if random.random() < epsilon:
            return random.randint(0, self.action_dim - 1)  # 以 epsilon 的概率随机选择动作（探索）
        state = torch.FloatTensor(state).unsqueeze(0).to(device)  # 将状态转换为张量
        with torch.no_grad():
            q_dist = self.policy_net(state)  # 获取 Q 值分布
            q_values = (q_dist * self.support).sum(2)  # 计算 Q 值的期望值
        return q_values.argmax(1).item()  # 选择 Q 值最大的动作（利用）

    def update(self):
        # 更新策略网络
        if len(self.memory) < 64:
            return  # 如果经验回放缓冲区中的样本不足，直接返回

        batch = self.memory.sample(64)  # 从经验回放缓冲区中随机采样一个批次
        states, actions, rewards, next_states, dones = zip(*batch)  # 解压批次数据

        # 将数据转换为张量并移动到设备（GPU 或 CPU）
        states = torch.FloatTensor(np.array(states)).to(device)
        actions = torch.LongTensor(actions).to(device)
        rewards = torch.FloatTensor(rewards).to(device)
        next_states = torch.FloatTensor(np.array(next_states)).to(device)
        dones = torch.FloatTensor(dones).to(device)

        with torch.no_grad():
            next_q_dist = self.target_net(next_states)  # 获取下一个状态的 Q 值分布
            next_actions = (next_q_dist * self.support).sum(2).argmax(1)  # 选择下一个状态的最佳动作
            next_q_dist = next_q_dist[range(64), next_actions]  # 获取下一个状态最佳动作的 Q 值分布

            # 扩展 rewards 和 dones 的维度，使其与支撑点的维度匹配
            rewards = rewards.unsqueeze(1).expand(-1, self.atoms)
            dones = dones.unsqueeze(1).expand(-1, self.atoms)

            # 计算 Tz（目标 Q 值分布）
            Tz = rewards + (1 - dones) * 0.99 * self.support
            Tz = Tz.clamp(self.v_min, self.v_max)  # 将 Tz 限制在 [v_min, v_max] 范围内

            # 计算投影分布
            b = (Tz - self.v_min) / self.delta_z  # 计算 Tz 对应的支撑点索引
            l = b.floor().long()  # 下界索引
            u = b.ceil().long()  # 上界索引
            l[(u > 0) * (l == u)] -= 1  # 处理边界情况
            u[(l < (self.atoms - 1)) * (l == u)] += 1  # 处理边界情况

            # 计算投影分布的偏移量
            offset = torch.linspace(0, (64 - 1) * self.atoms, 64).long().unsqueeze(1).expand(64, self.atoms).to(device)
            proj_dist = torch.zeros_like(next_q_dist)  # 初始化投影分布
            proj_dist.view(-1).index_add_(0, (l + offset).view(-1), (next_q_dist * (u.float() - b)).view(-1))  # 计算下界贡献
            proj_dist.view(-1).index_add_(0, (u + offset).view(-1), (next_q_dist * (b - l.float())).view(-1))  # 计算上界贡献

        q_dist = self.policy_net(states)  # 获取当前状态的 Q 值分布
        log_q_dist = torch.log(q_dist[range(64), actions])  # 计算当前动作的对数概率
        loss = -(proj_dist * log_q_dist).sum(1).mean()  # 计算损失函数（交叉熵损失）

        self.optimizer.zero_grad()  # 清空梯度
        loss.backward()  # 反向传播
        self.optimizer.step()  # 更新策略网络参数

    def update_target(self):
        # 更新目标网络的权重
        self.target_net.load_state_dict(self.policy_net.state_dict())

最后是训练方法，这个就很容易了：

def train():
    env = gym.make("CartPole-v1", render_mode="human")
    agent = RainbowAgent(4, 2)
    episode_rewards = []

    for episode in range(60):
        state, _ = env.reset()
        total_reward = 0
			
        # 一场游戏的时长，这里为200
        for step in range(200):
            action = agent.act(state)
            next_state, reward, done, _, _ = env.step(action)
            agent.memory.push(state, action, reward, next_state, done)
            state = next_state
            total_reward += reward

            agent.update()

            if done:
                break

        episode_rewards.append(total_reward)
        print(f"Episode {episode + 1}, Reward: {total_reward}")

        if episode % 10 == 0:
            agent.update_target()

    # 绘制奖励曲线
    plt.plot(episode_rewards)
    plt.xlabel("Episode")
    plt.ylabel("Reward")
    plt.title("Rainbow Training Curve")
    plt.show()

然后进行简单的等待就可以看到结果了。

出于个人爱好，我又绘制了价值曲线：

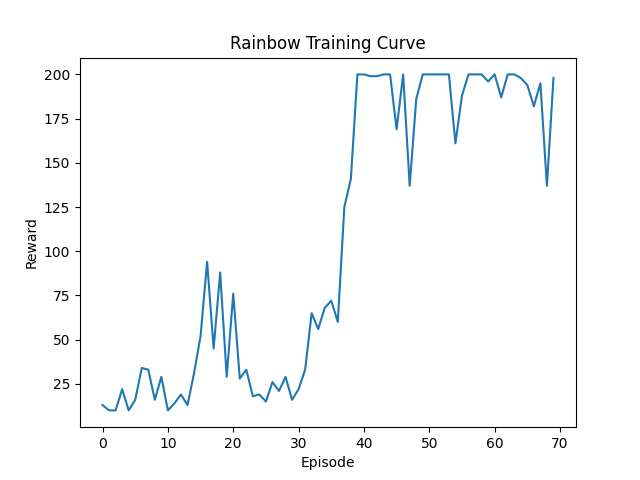
可以看到后来的价值取决于游戏时长了，整场游戏完全站住的价值就是200。

DDPG

DDPG也叫深度确定性策略梯度，他与PG（策略梯度）、DPG（确定性策略梯度）同属于梯度上升优化方法，且他们均适用于连续的动作空间（PG也可以用与离散空间），DDPG的特点就是非常适用与机器人控制，比如一个拥有较高自由度的机械设备，哪怕进行粗糙的离散化都会有$3^n$个动作空间，这对DQN等离散网络来将几乎是噩梦，所以DDPG也是一种基于AC的方法，其可以在高维连续空间进行学习。

首先分析DQN之所以能过够稳定且稳健的逼近价值函数关键有两个要素：

• 网络具有经验池，可以随机抽取样本进行离轨学习
• 采用Q网络训练，在TD过程提供一直的目标

对DDPG，它采用了批量归一化(和RainBow一样)，同时也包含了一个AC架构。

许多的强化学习方法都包含了贝尔曼方程，这时必须的，根据原文所述我们可以把一个策略不确定的递归关系如：

$$Q^\pi(s_t,a_t)=E[r(s_t,a_t)+\gamma E[Q^\pi(s_{t+1},a_{t+1})]]$$

然后确定一个策略，将其描述为$\mu$并省去嵌套的期望计算：

$$Q^\mu(s_t,a_t)=E[r(s_t,a_t)+\gamma Q^\mu(s_{t+1},\mu (s_{t+1}))]$$

对于Q学习常用贪婪策略结合深度神经网络进行函数逼近，可以设定一个损失函数将进行优化，假设网络参数$\theta$：

$$L(\theta^Q)=E[(Q(s_t,a_t|\theta^Q)-y_t)^2]$$

虽然$y_t$也包含了$\theta^Q$项，但是它通常被忽略。

---

策略梯度的概念在第一节就已经说过强化学习网络与机器人控制——数学基础。简单概括策略梯度其实就是对偏差的一种更好的描述，这种描述对价值函数进行梯度上升得到一个局部最优解，我们在这个过程中仅优化一个中间变量，这就是所谓的策略梯度，而引入策略梯度就是为了保证神经网络的泛化能力。

而使用策略梯度的方法都被称为策略-评判法，也就是Actor-Criris方法。

在文献中指出，Q学习的损失函数是被证明不稳定的，所以Q很容易发散，论文就提出了一种软更新方法，通过创建AC网络的副本按照一定的权重拷贝参数，这与知识蒸馏有几分相似，只不过一个是对权重进行缓慢更新，而知识蒸馏是模仿教师网络输出进行的更新，以此学习。

初次之外，在从低维度特征向量观测值中学习时，范围可能会因为环境而异。这可能会让网络难以学习，为此论文也用了批量归一化，让小批量中的每个维度进行归一化处理，均值为零且方差为一。

类似的作者也引入了重放缓冲区用于离线学习，正如优化算法的常用假设即样本不相干，也就是说样本需要在环境中探索生成，但是这与不相干假设不成立，而且为了提高硬件效率，必须要以小批量的方式进行学习。重放缓冲区其实就是一个SARS的队列，其空间大小有限，又由于DDPG时离轨策略，所以这个缓冲区又可以很大。

最后网络引入了一个过程噪声N，从而构建策略，只需要输出增加这个噪声即可，这个噪声必须是一个与环境有关，所以作者使用了Unlenbeck & Ornstein噪声，也叫OU噪声。下面是我们实现的DDPG网络模型：

# OU噪声类
class OUNoise:
    def __init__(self, action_dim, mu=0.0, theta=0.15, sigma=0.2):
        self.theta = theta
        self.sigma = sigma
        self.mu = mu * np.ones(action_dim)
        self.state = np.copy(self.mu)  # 初始化state属性
        self.current_noise = 0.0  # 添加current_noise属性用于日志记录

    def reset(self):
        self.state = np.copy(self.mu)
        self.current_noise = 0.0

    def sample(self):
        dx = self.theta * (self.mu - self.state)
        dx += self.sigma * np.random.randn(len(self.state))
        self.state += dx
        self.current_noise = np.mean(np.abs(dx))  # 更新当前噪声水平
        return self.state


# 演说家
class Actor(nn.Module):
    def __init__(self, state_dim, action_dim, max_action):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(state_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU(),
            nn.Linear(128, action_dim),
            nn.Tanh()
        )
        self.max_action = max_action

    def forward(self, state):
        return self.net(state) * self.max_action


# 评论家
class Critic(nn.Module):
    def __init__(self, state_dim, action_dim):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(state_dim + action_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU(),
            nn.Linear(128, 1)
        )

    def forward(self, state, action):
        return self.net(torch.cat([state, action], dim=1))


# 经验池(一般都需要很大)
class ReplayBuffer:
    def __init__(self, max_size=1e6):
        self.buffer = deque(maxlen=int(max_size))
        self.max_size = max_size  # 添加max_size属性

    def push(self, state, action, reward, next_state, done):
        self.buffer.append((state, action, reward, next_state, done))

    def sample(self, batch_size):
        if len(self.buffer) < batch_size:
            raise ValueError("Not enough samples in buffer")

        batch = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*batch)
        return (
            np.array(state),
            np.array(action),
            np.array(reward),
            np.array(next_state),
            np.array(done)
        )

    def __len__(self):
        return len(self.buffer)

首先是基本模块，包括AC层、经验池与OUNoise（Ornstein-Uhlenbeck噪声），下面给出一个画的非常不错的图用于展示DDPG的结构层次：

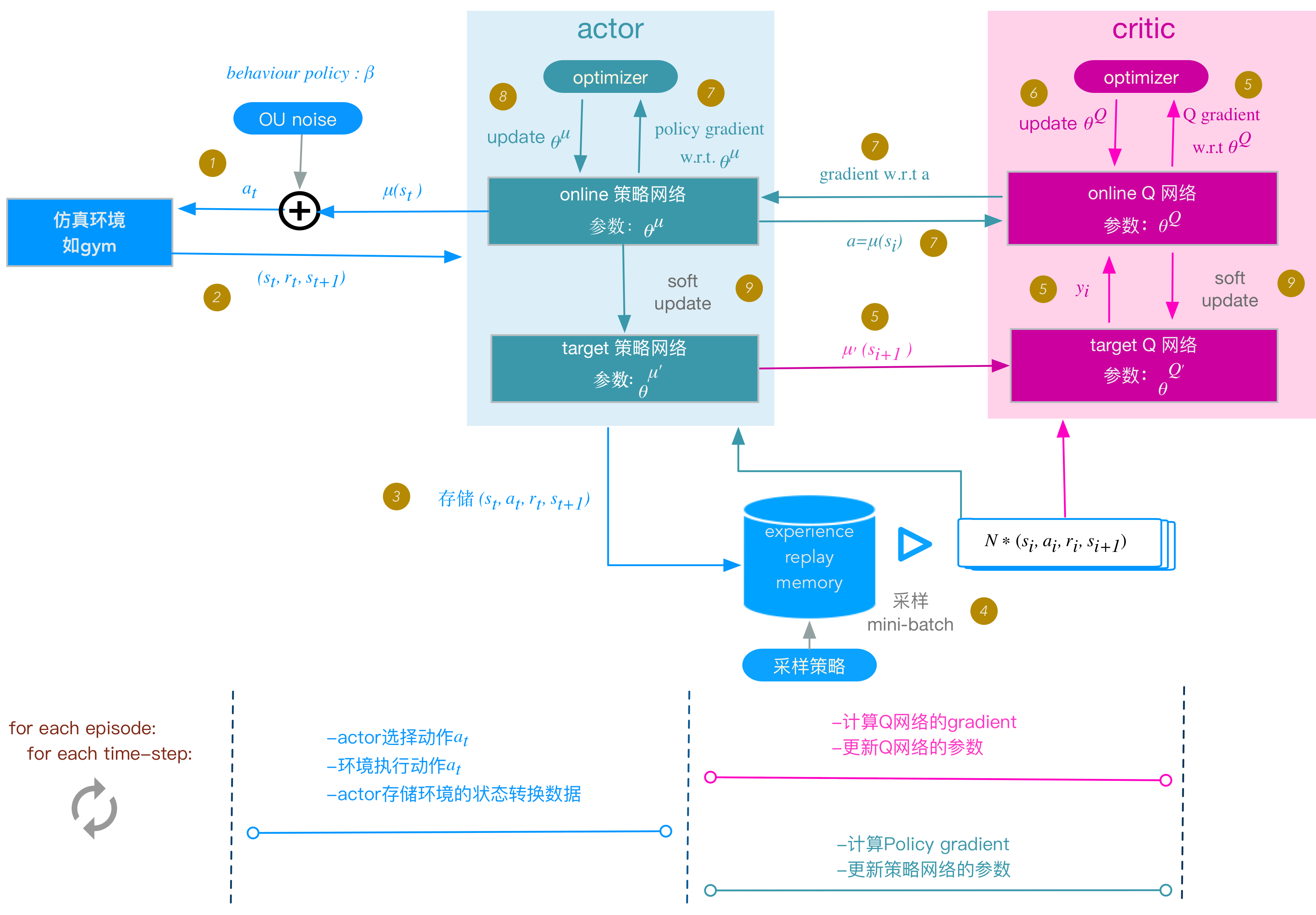
我们可以看到采取行动时会引入一个噪声，同时AC网络也有对应的软更新网络等等。下面就把网络组合起来：

class DDPG:
    def __init__(self, state_dim, action_dim, max_action, device=None):
        if device is None:
            self.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
        else:
            self.device = device

        self.max_action = max_action  # 添加max_action属性
        self.state_dim = state_dim  # 添加state_dim属性
        self.action_dim = action_dim  # 添加action_dim属性

        # 初始化网络
        self.actor = Actor(state_dim, action_dim, max_action).to(self.device)
        self.critic = Critic(state_dim, action_dim).to(self.device)
        self.target_actor = Actor(state_dim, action_dim, max_action).to(self.device)
        self.target_critic = Critic(state_dim, action_dim).to(self.device)

        # 目标网络硬更新
        self.hard_update(self.target_actor, self.actor)
        self.hard_update(self.target_critic, self.critic)

        # 优化器
        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=1e-4)
        self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=1e-3)
        self.criterion = nn.MSELoss()

        # 经验回放和噪声
        self.replay_buffer = ReplayBuffer()
        self.noise = OUNoise(action_dim)
        self.batch_size = 64
        self.gamma = 0.99
        self.tau = 0.005
        self.total_updates = 0

    def hard_update(self, target, source):
        """硬更新目标网络"""
        for target_param, source_param in zip(target.parameters(), source.parameters()):
            target_param.data.copy_(source_param.data)

    def update(self):
        if len(self.replay_buffer) < self.batch_size:
            return

        # 从回放缓冲区采样
        state, action, reward, next_state, done = self.replay_buffer.sample(self.batch_size)

        # 转换为张量
        state = torch.FloatTensor(state).to(self.device)
        action = torch.FloatTensor(action).to(self.device)
        reward = torch.FloatTensor(reward).unsqueeze(1).to(self.device)
        next_state = torch.FloatTensor(next_state).to(self.device)
        done = torch.FloatTensor(done).unsqueeze(1).to(self.device)

        # Critic更新
        with torch.no_grad():
            target_actions = self.target_actor(next_state)
            target_q = self.target_critic(next_state, target_actions)
            target_q = reward + (1 - done) * self.gamma * target_q

        current_q = self.critic(state, action)
        critic_loss = self.criterion(current_q, target_q)

        self.critic_optimizer.zero_grad()
        critic_loss.backward()
        torch.nn.utils.clip_grad_norm_(self.critic.parameters(), 1.0)
        self.critic_optimizer.step()

        # Actor更新
        actor_actions = self.actor(state)
        actor_loss = -self.critic(state, actor_actions).mean()

        self.actor_optimizer.zero_grad()
        actor_loss.backward()
        torch.nn.utils.clip_grad_norm_(self.actor.parameters(), 1.0)
        self.actor_optimizer.step()

        # 目标网络软更新
        self.soft_update(self.target_actor, self.actor)
        self.soft_update(self.target_critic, self.critic)

        self.total_updates += 1

    def soft_update(self, target, source):
        """软更新目标网络"""
        for target_param, source_param in zip(target.parameters(), source.parameters()):
            target_param.data.copy_(self.tau * source_param.data + (1.0 - self.tau) * target_param.data)

    def select_action(self, state, add_noise=True):
        self.actor.eval()
        state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
        with torch.no_grad():
            action = self.actor(state)
        self.actor.train()

        if add_noise:
            noise = torch.FloatTensor(self.noise.sample()).to(self.device)
            action += noise

        return action.clamp(-self.max_action, self.max_action).cpu().numpy().flatten()

给出训练和测试方法，并开始运行：

def train(env, agent, num_episodes=300, max_steps=200):
    # 初始化自适应噪声包装器
    reward_history = []

    # 改进的预填充阶段
    print(">> Pre-filling buffer with demo trajectories...")
    state = env.reset()[0]
    while len(agent.replay_buffer) < 10000:  # 保证足够初始数据
        # 生成包含人工引导的示范数据
        if np.random.rand() < 0.3:  # 30%概率生成示范动作
            theta = np.arctan2(state[1], state[0])
            ang_vel = state[2]
            # 简单的反向控制策略
            demo_action = [-0.5 * theta - 0.1 * ang_vel]
        else:
            demo_action = env.action_space.sample()

        next_state, reward, done, _, _ = env.step(demo_action)
        agent.replay_buffer.push(state, demo_action, reward, next_state, done)
        state = next_state if not done else env.reset()[0]

    # 主训练循环
    best_avg_reward = -float('inf')
    for ep in range(num_episodes):
        state = env.reset()[0]
        episode_reward = 0
        step_counts = 0

        for step in range(max_steps):
            # 动态动作选择
            base_action = agent.select_action(state)
            noisy_action = np.clip(
                base_action,
                -agent.max_action * 0.9,
                agent.max_action * 0.9
            )

            next_state, reward, done, _, _ = env.step(noisy_action)

            # 优先经验存储策略
            theta = np.arctan2(next_state[1], next_state[0])
            ang_vel = next_state[2]
            if abs(theta) > 0.8 or abs(ang_vel) > 3.0:
                for _ in range(2):
                    agent.replay_buffer.push(state, noisy_action, reward, next_state, done)
            else:
                agent.replay_buffer.push(state, noisy_action, reward, next_state, done)

            # 条件更新策略
            if step % 2 == 0 and len(agent.replay_buffer) > 10000:
                agent.update()

            episode_reward += reward
            state = next_state
            step_counts += 1

            if done:
                break

        # 动态参数调整
        reward_history.append(episode_reward)
        avg_reward = np.mean(reward_history[-20:])

        # 训练日志增强
        print(
            f"Ep {ep + 1:03d} | Reward: {episode_reward:7.1f} | "
            f"Avg20: {avg_reward:7.1f} | "
            f"Noise: {agent.noise.current_noise:.2f} | "  # 修改为直接访问noise属性
            f"LR: {agent.actor_optimizer.param_groups[0]['lr']:.2e}"
        )


def test(agent, env_name='Pendulum-v1'):
    env = gym.make(env_name, render_mode='human')
    state, _ = env.reset()
    step = 0

    while True:
        action = agent.select_action(state, add_noise=False)
        next_state, _, done, _, _ = env.step(action)
        state = next_state
        step += 1
        time.sleep(0.02)
        if step > 500000:
            state, _ = env.reset()

    env.close()
    
if __name__ == "__main__":
    # 创建环境
    env = gym.make('Pendulum-v1')

    # 设置设备
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    print(f"Using device: {device}")

    # 初始化DDPG智能体
    agent = DDPG(
        state_dim=env.observation_space.shape[0],
        action_dim=env.action_space.shape[0],
        max_action=float(env.action_space.high[0]),
        device=device
    )

    # 训练智能体
    train(env, agent, num_episodes=200)

    # 测试训练好的智能体
    test(agent)

运行一下就会发现：

Ep 001 | Reward: -1466.4 | Avg20: -1466.4 | Noise: 0.14 | LR: 1.00e-04
Ep 002 | Reward: -1669.1 | Avg20: -1567.8 | Noise: 0.36 | LR: 1.00e-04
Ep 003 | Reward: -1660.9 | Avg20: -1598.8 | Noise: 0.11 | LR: 1.00e-04
Ep 004 | Reward: -1649.1 | Avg20: -1611.4 | Noise: 0.08 | LR: 1.00e-04
Ep 005 | Reward: -1618.1 | Avg20: -1612.7 | Noise: 0.11 | LR: 1.00e-04
Ep 006 | Reward: -1490.5 | Avg20: -1592.3 | Noise: 0.23 | LR: 1.00e-04
Ep 007 | Reward: -1527.1 | Avg20: -1583.0 | Noise: 0.15 | LR: 1.00e-04
Ep 008 | Reward: -1446.7 | Avg20: -1566.0 | Noise: 0.27 | LR: 1.00e-04
Ep 009 | Reward: -1449.3 | Avg20: -1553.0 | Noise: 0.14 | LR: 1.00e-04
Ep 010 | Reward: -1484.1 | Avg20: -1546.1 | Noise: 0.03 | LR: 1.00e-04
Ep 011 | Reward: -1511.7 | Avg20: -1543.0 | Noise: 0.05 | LR: 1.00e-04
Ep 012 | Reward: -1299.2 | Avg20: -1522.7 | Noise: 0.02 | LR: 1.00e-04
Ep 013 | Reward: -1582.6 | Avg20: -1527.3 | Noise: 0.02 | LR: 1.00e-04
Ep 014 | Reward: -1288.7 | Avg20: -1510.2 | Noise: 0.01 | LR: 1.00e-04
Ep 015 | Reward: -1079.4 | Avg20: -1481.5 | Noise: 0.26 | LR: 1.00e-04
Ep 016 | Reward:  -945.3 | Avg20: -1448.0 | Noise: 0.19 | LR: 1.00e-04
Ep 017 | Reward:  -914.7 | Avg20: -1416.6 | Noise: 0.28 | LR: 1.00e-04
Ep 018 | Reward: -1039.9 | Avg20: -1395.7 | Noise: 0.25 | LR: 1.00e-04
Ep 019 | Reward:  -891.1 | Avg20: -1369.1 | Noise: 0.65 | LR: 1.00e-04
Ep 020 | Reward:  -846.7 | Avg20: -1343.0 | Noise: 0.16 | LR: 1.00e-04
...
Ep 046 | Reward:  -247.9 | Avg20:  -593.7 | Noise: 0.01 | LR: 1.00e-04
Ep 047 | Reward:  -244.7 | Avg20:  -536.3 | Noise: 0.18 | LR: 1.00e-04
Ep 048 | Reward:  -259.8 | Avg20:  -497.6 | Noise: 0.08 | LR: 1.00e-04
Ep 049 | Reward:  -127.4 | Avg20:  -462.7 | Noise: 0.11 | LR: 1.00e-04
Ep 050 | Reward:  -118.5 | Avg20:  -423.3 | Noise: 0.18 | LR: 1.00e-04
Ep 051 | Reward:  -128.8 | Avg20:  -391.1 | Noise: 0.21 | LR: 1.00e-04
Ep 052 | Reward:  -126.9 | Avg20:  -365.7 | Noise: 0.15 | LR: 1.00e-04
Ep 053 | Reward:  -122.1 | Avg20:  -341.2 | Noise: 0.24 | LR: 1.00e-04
Ep 054 | Reward:  -354.7 | Avg20:  -326.9 | Noise: 0.32 | LR: 1.00e-04
Ep 055 | Reward:  -117.2 | Avg20:  -305.5 | Noise: 0.02 | LR: 1.00e-04
Ep 056 | Reward:  -353.7 | Avg20:  -297.7 | Noise: 0.09 | LR: 1.00e-04
Ep 057 | Reward:  -127.2 | Avg20:  -270.1 | Noise: 0.02 | LR: 1.00e-04
Ep 058 | Reward:  -118.1 | Avg20:  -250.6 | Noise: 0.30 | LR: 1.00e-04
Ep 059 | Reward:    -0.9 | Avg20:  -221.3 | Noise: 0.04 | LR: 1.00e-04
...
Ep 123 | Reward:  -116.9 | Avg20:  -144.8 | Noise: 0.00 | LR: 1.00e-04
Ep 124 | Reward:  -119.9 | Avg20:  -144.8 | Noise: 0.05 | LR: 1.00e-04
Ep 125 | Reward:  -241.9 | Avg20:  -150.8 | Noise: 0.20 | LR: 1.00e-04
Ep 126 | Reward:  -125.5 | Avg20:  -150.8 | Noise: 0.32 | LR: 1.00e-04

可以看到在100轮内肯定会收敛，其表达效果就是小摆锤会被来回切换扭矩，在0处高频震荡，或者存在一定静差

总结

本期博客介绍了DDPG和Rainbow，内容进行了一些修改，尤其是对问题描述与网络特点，同时代码也修改了一些bug。