机器人学基础——控制理论

标准型

博客开始前，我们必须掌握一些基础知识。首先提及标准型，我们必须要说一下线性系统的状态方程：

$$\dot x=Ax+Bu\tag{1.1}$$

这是一个简单的状态转移方程，我们可以简单的理解这个系统为一个微分方程、线性系统、差分方程。不过归根结底，我们都是把系统变量x进行了迭代，而u作为输入变量自然就是我们提供的外界激励

然后我们把系统输出进行了一次传递即：

$$y=Cx+Du\tag{1.2}$$

其中的x就是系统变量x，u为外界提供的激励，几乎所有的，都会把D看作为0，这样更加方便理解。

而1.1与1.2式就是我们的状态方程，其中的A、B、C、D均为矩阵，x、u为有限维度的向量

---

对于上面的方程我们可以进行一些简单的化简，使其变成Y-Z的形式：

我们假设有一个变量z，他是与x的另一个关系，我们可以对A进行非奇异分解，或者说谱分解，求出对应的特征向量矩阵T，然后写作：

$$\dot z=T^{-1}ATz+T^{-1}Bu\tag{1.3}$$

而约旦矩阵就可以写作：

$$J=T^{-1}AT\tag{1.3.1}$$

当然这么做有一个前提，那就是A的特征值互异（也就是非奇异），我们可以对1.2式也如此处理：

$$y=CTz+DTu$$

通常D当作0看待，我们可以写作最终形式：

$$y=CTz\tag{1.4}$$

当然这个系统的可控性可以根据输入项的系数是否与z同秩来判断，即判断$T^{-1}B$是否有一行所有元素的和为0，有的话则系统不可控，反之可控。这种表达方式顺便可以判断能控性！感觉很不错，那么我们还有没有其他方法呢？答案是有的。

拉格朗日动力学方程

在《数学物理方法》种，对物理模型的数学化进行了很详细的解答，我们这里也需要用到相似的知识去判断，这里就需要引入拉格朗日动力学方程了，不同于能量守恒方程：封闭系统内动能和势能总和保持不变，我们引入了广义力，我们假设系统的总动能为T，总势能为V，我们有：

$$L=T-V\tag{2.1}$$

L也叫做拉格朗日量，我们总有一个方程：

$$\frac{\partial}{\partial t}\frac{\partial L}{\partial \dot q}-\frac{\partial L}{\partial q}=Q\tag {2.2}$$

而q这个变量我们可以看作是描述目标的全部信息，比如一个包含了位置，速度，角度的向量，或者是一个点的坐标，而$\dot q$为q对时间微分，可以理解为瞬时变化量，比如q是位置则瞬时变化率为速度。q为速度则瞬时变化率为加速度，其为对t的导数。我们可以举个例子：

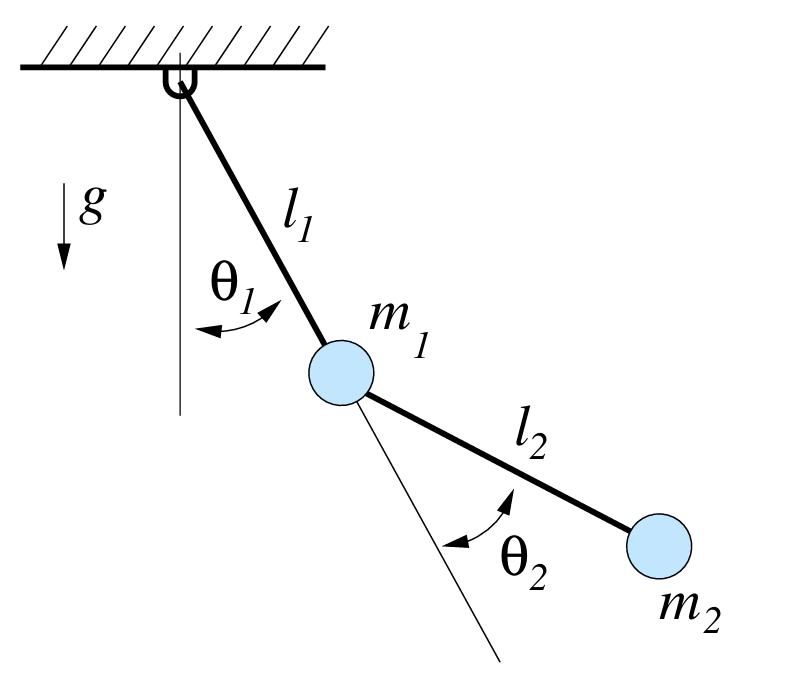
对于这个系统我们可以描述出两个小球的坐标，对于第一个小球而言，他的位置向量为：

$$x_1=\left[\begin{matrix} l_1sin\theta_1\\ -l_1cos\theta_1 \end{matrix} \right]\tag {2.3}$$

对于第二个球，我们可以在第一个球的基础上进行平移，即：

$$x_2=x_1+\left[\begin{matrix} l_2sin(\theta_1+\theta_2)\\ -l_2cos(\theta_1+\theta_2) \end{matrix} \right]\tag {2.4}$$

对这两个点求导，得到：

$$\dot x_1=\left[\begin{matrix} l_1\dot \theta_1cos\theta_1\\ l_1\dot \theta_1sin\theta_1 \end{matrix} \right]\tag {2.5}$$ $$\dot x_2=\dot x_1+\left[\begin{matrix} l_2(\dot \theta_1+\dot \theta_2)cos(\theta_1+\theta_2)\\ l_2(\dot \theta_1+\dot \theta_2)sin(\theta_1+\theta_2) \end{matrix} \right]\tag {2.6}$$

我们发现这个方程用于描述位置可以通过角度$\theta$去表示，我们就可以用q代替对应的$\theta$去书写了：即$q_1=\theta1,q_2=\theta2$，我们列写动能和势能：

$$T=\frac{1}{2}\dot x_1^Tm_1\dot x_1 + \frac{1}{2}\dot x_2^Tm_2\dot x_2\tag{2.7}$$

这里注意采用二次型去表达平方，而动能是：

$$\frac{1}{2}mv^2$$

我们展开2.7式得到：

$$T=\frac{1}{2}(m_1+m_2)l_1^2\dot q_1^2+\frac{1}{2}m_2l_2^2 (\dot q_1 + \dot q_1)^2 + m_2l_1l_2\dot q_1(\dot q_1+\dot q_2)cosq_2\tag{2.8}$$ $$U=-(m_1+m_2)gl_1cosq_1-m_2gl_2cos(q_1+q_2)\tag{2.9}$$

我们做差求对$\dot q$的导数（注意，此变量不是q，所以我们求偏导数需要把q当作常数进行求导），接下来直接求导：

$$\frac{\partial L}{\partial \dot q_1}=(m_1+m_2)l_1^2\dot q_1+m_1l_2^2(\dot q_1+\dot q_2)+2m_2l_1l_2\dot q_1cos q_2+m_2l_1l_2\dot q_2cosq_2\tag{2.10}$$

我们再对求：

$$\frac{\partial L}{\partial q_1}=-(m_1+m_2)gl_1sinq_1+m_2gl_2sin(q_1+q_2)\tag{2.11}$$

我们对2.10对时间求导，也就是让所有的q进行升阶：

$$\frac{\partial}{\partial t}\frac{\partial L}{\partial \dot q_1}=(m_1+m_2)l_1^2\ddot q_1+m_2l_2^2(\ddot q_1+\ddot q_2)+m_2l_1l_2(2\ddot q_1+\ddot q_2)cosq_2-m_2l_1l_2(2\dot q_1+\dot q_2)\dot q_2sinq_2\tag{2.12}$$

我们带入2.12与2.11代入2.1式得到：

$$\begin{equation}\begin{split} \tau_1=(m_1+m_2)l_1^2\ddot q_1+m_2l_2^2(\ddot q_1+\ddot q_2)+m_2l_1l_2(2\ddot q_1+\ddot q_2)cosq_2\\ -m_2l_1l_2(2\dot q_1+\dot q_2)\dot q_2sinq_2+(m_1+m_2)gl_1sinq_1+m_2gl_2sin(q_1+q_2) \end{split}\end{equation}\tag{2.13}$$

其中的$\tau$就是我们的广义力Q，只是进行简单的字母表达，同理对于$q_2$我们重复上述步骤得到：

$$m_22l_2^2(\ddot q_1+\ddot q_2)+m_2l_1l_2\ddot q_1cosq_2+m_2l_1l_2\dot q_1^2sinq_2+m_2gl_2sin(q_1+q_2)=\tau_2\tag{2.14}$$

对于2.13与2.14两个惊人庞大的式子，我们发现这个二阶倒立摆是一个二阶系统，我们可以写作几个矩阵的乘法：

$$H(q)\ddot q+C(q,\dot q)\dot q+G(q)=B(q)u$$

这里面涉及了几个非常重要的变量，H叫做惯性矩阵，C叫做科里奥利力，G叫做重力，B作为控制输入信号的矩阵

科里奥利力也可以叫他地转偏向力，对于旋转的系统，这个力起到速度项的修正作用

我们列些一下这些矩阵的值：

$$H(q)=\left[\begin{matrix} (m_1+m_2)l_1^2+m_2l_2^2+2m_2l_1l_2cosq_2 & m_2l_2^2+m_2l_1l_2cosq_2\\ m_2l_2^2+m_2l_1l_2cosq_2&m_2l_2^2 \end{matrix} \right]\tag {2.15}$$ $$C(q,\dot q)=\left[\begin{matrix} 0 & -m_2l_1l_2(2\dot q_1+\dot q_2)sinq_2\\ m_2l_1l_22\dot q_1sinq_2 & 0 \end{matrix} \right]\tag {2.15}$$ $$G(q)=g\left[\begin{matrix} (m_1+m_2)l_1sinq_1+m_2l_2sin(q_1+q_2)\\ m_2l_2sin(q_1+q_2) \end{matrix} \right]\tag {2.15}$$

注意，g为重力加速度。我们发现一个规律，就是二阶系统都可以用这种方式表达，而且对于一个二阶阻尼震荡系统，我们也可以用此法表达。

反馈线性化

注意，反馈线性化是一个非常重要的知识，我们无法或者很难控制一个非线性系统，我们总在尽力的逼近这个系统，所以我们有没有办法让反馈尽可能的线性化呢？答案是有的，这就是反馈线性化，反馈线性化的精髓在于把状态空间看作一个流形（注意，流形可以简单看作各点导数连续的几何体），我们分析流形的向量场就可以进行线性化操作：

$$\dot x=Fx+Gu\tag{3.1}$$ $$y=Hx\tag{3.2}$$

我们在3.1和3.2这种状态空间表达式中进行推导，在仿射非线性系统中，系统的状态空间表现为非线性， 而控制输入则为线性的。假设存在一个同胚变化T可以线性化此矩阵我们需要用李代数的左扰模型进行矩阵求导：

定义李代数算符为$\nabla$:

$$\dot y=\nabla H_xFx+\nabla H_xGu\tag {3.3}$$

其中:$\nabla H_x$为H对x的导数，叫他李导数即可。我们如此做仅仅是因为泰勒展开的多项式逼近方法，通过这种办法进行的逼近精度在接收范围，通过有限步进行缩小误差，这样可以得到精确的反馈信号。

现在假设u为输入系统变量，我们假设真实系统输入为v，u包括了反馈内容，假设$\dot y=v$，那么解的u为：

$$u=\frac{1}{\nabla H_xG}(-\nabla H_xF+v)\tag {3.4}$$

这样就保证了反馈的线性化。当然这是一种简单的方法，我们可以通过分析$\nabla H_xG、\nabla H_xF$的李括号向量场分析是否可以充分线性化，也就是说：

$$gard=[\nabla H_xF,\nabla H_xG]=\nabla H_xG·F-\nabla H_xF·G$$

通过判断此向量场的秩是否与输入维度一样，如果相同则可以线性化，反之则不能。

能控性、能观性

首先对这两个性质下个定义：

• 能观性：给定输入，任意的初始状态都能被系统的输出唯一确定。
• 能构性：给定输入，任意的最终状态都能被系统的输出唯一确定。

这两个性质很好去判断，这里采用了Sylvester’s定理，这里假设我们的系统是1.1和1.2式我们可以假设两个矩阵分别为能控性和能观性观察矩阵：

$$M=\left[\begin{matrix} B&AB&A^2B&A^3B&...&A^nB \end{matrix} \right]_{n×n}\tag {4.1}$$ $$N=\left[\begin{matrix} C\\ CA\\ CA^2\\ CA^3\\ ...\\ CA^n \end{matrix} \right]_{n×n}\tag {4.2}$$

我们通过判断4.1与4.2矩阵的维度就可以判断系统的能控性和能观性了，即如果M的维度或者N的维度不是n的话，那就不能控或者不能观。

李雅普诺夫方法

到目前位置，我们还没有一个非常好用的稳定性判据，在自控原理书中给出了劳斯判据和奈奎斯特判据，但是这些判据建立在复平面传递函数上，没办法更加通用化，我们就不得不提到李雅普诺夫方法，在高等数学中，我们学极限一定接触了$\epsilon-\delta$语言，这是一种小常量的逼近描述，对于一个系统而言，我们自然也可以表达：一个系统在一个很小很小的范围震荡，我们说他是稳定的即：

状态空间一点$x$，距离$x_e$的范数满足：$对于任意的\epsilon>0，存在\delta>0使得x,x_e∈U(\delta),则x有界，也可以写作:$

$$||x-x_e||<\epsilon$$

李雅普诺夫稳定除了有界的稳定还可以分为线性渐进稳定和指数渐进稳定，分别表达为：

$$x(0)=x^*+\epsilon得到x(\infty)=x^*$$ $$x(0)=x^*+\epsilon得到(x(t)-x^*)<Ce^{-\alpha}t$$

当然这也可以解释上面李导数的向量场与输入维度一样，李氏梯度场会收敛。

李雅普诺夫第一法

我们在复平面分析传递函数时知道了，如果传递函数的所有极点位于左半平面，传递函数稳定，我们可以把一个线性系统(1.1和1.2)改造：

$$W(s)=C(sI-A)^{-1}B\tag{5.1}$$

分析W(s)的开环零极点即可（这个方法很朴素）

李雅普诺夫第二法

我们可以设定一个标量函数V(x)，通过V的正定和负定进行判断，那么如何设置这样的标量函数呢？答案很简单，我们可以假设一个矩阵P，使：

$$V(x)=x^TPx\tag{5.2}$$

即可，而V的符号可以由P来判断，这便是希尔维斯判，并且系统的稳定在处在$x_e=0$处，我们可以从标量函数分析系统的稳定方式：

1、判断V(x)的方向，也就是计算V是正定还是负定，只有V是正定，V的一阶导是负定，系统才能稳定

2、如果满足条件1，那么当x趋近于无穷时，V也趋近于无穷

为了方便寻找这样的V，我们统一规定一些函数，对于线性定常方程即：

$$\dot x(t)=Ax(t)\tag{5.3}$$

我们假设这个标量函数是4.1式，我们求导得到：

$$\dot V(x)=\dot x^TPx+x^TP\dot x\tag{5.4}$$

把4.3代入4.4中得到：

$$(Ax)^TPx+x^TPAx\tag{5.5}$$

进一步打开得到：

$$x^TAPx+x^TPAx\tag{5.6}$$

提出全部的x得到：

$$x^T(A^TP+PA)x\tag{5.7}$$

我们就可以把中间的式子看作新的变量Q，我们分析：

$$Q=-(A^TP+PA)\tag{5.8}$$

如果Q是正定，4.7式应为负定，V的一阶导为负定，系统稳定。所以如果我们假设一个Q为单位矩阵I，如果可以反向推出一个P，那么系统稳定，我们可以连续写作：

$$A^TP+PA=-Q=-I\tag{5.9}$$

此法几乎万能，我们可以大肆使用。

总结

本期博客介绍了现代控制基础分析方法，通过这些内容，读者可以了解基本的分析方法，读者可以逐步的理解系统分析方法。