随机数怎么样随机的

介绍

都说计算机的随机都是伪随机，其实无论是生活的各个角落都是伪随机而不是真随机，真随机可能真的不存在，所有的事件都可以用简单的P(A)表示，无论是否有条件，那么我们如果实现这种随机呢？

随机算法

随机数对人来说可能是随机的也可能不是，处于量子态，不过目前的计算机所生成的随机数其实不算真随机，而是一种周期很大的循环数，那这样的数怎么生成呢？

线性同余法[LCG]

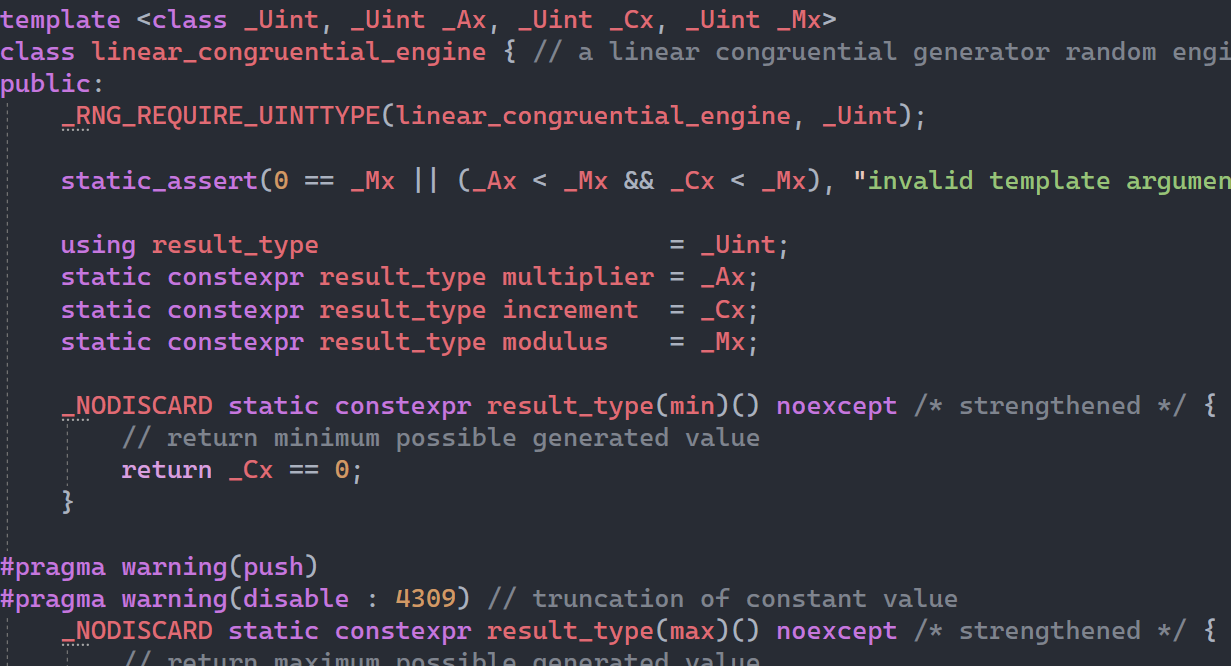
这种方法较为常用，在《C primer plus》中介绍了一段魔术语句，可以实现随机数，那么很多人可能好奇为什么这串代码可以生成随机数，这些已知的数字都是什么含义等等。

1
2
3

int m_rand(int seed){
    return (214013*seed+2531011)>>16&((1<<15)-1);
}

其实学过数学的人都对这种Ax+B的格式不陌生，一般都以线性开头命名，即线性同余算法，这种算法用通式表示为：
$$
seed = (A * seed + B) % C
$$
其中最大周期为C，A、B均为整数且C的所有因数中的质数都可以被A-1整除，即满足C%(A-1)==0

对于A、B是经过计算得到的，通过移位运算不难算出重复周期为2^15-1即(1<<15)-1。代码中的种子常使用时间。在C++的Random头文件中使用了这种算法。

平方取中法

这个算法的爹是冯诺依曼，算法主要讲的是：给定一个m位数记作x，其中m是偶数（基数计算带分数），计算x的平方，得到2m位数（不足在首端补0）然后从乘数中间得到m位数，然后重复这一步骤。

梅森旋转(Mersenne Twister)算法

衡量梅森旋转(MT)的质量，需要使用K分布，K分布的定义是：一个周期为T的随机序列Xi，每一位都有w位，当满足下面条件就成为w位的K分布

假设f(x)表示x的前v位形成的数字，并且长度为P的kv位序列：

($f(x_i)$，$f(x_{i+1})$，$f(x_{i+2})$…….$f(x_{i+k-1})$)

其中每个可能出现的$2^{kv}$组合在一个周期内出现相同的次数（除全0序列出现次数次数比其他序列少1次）

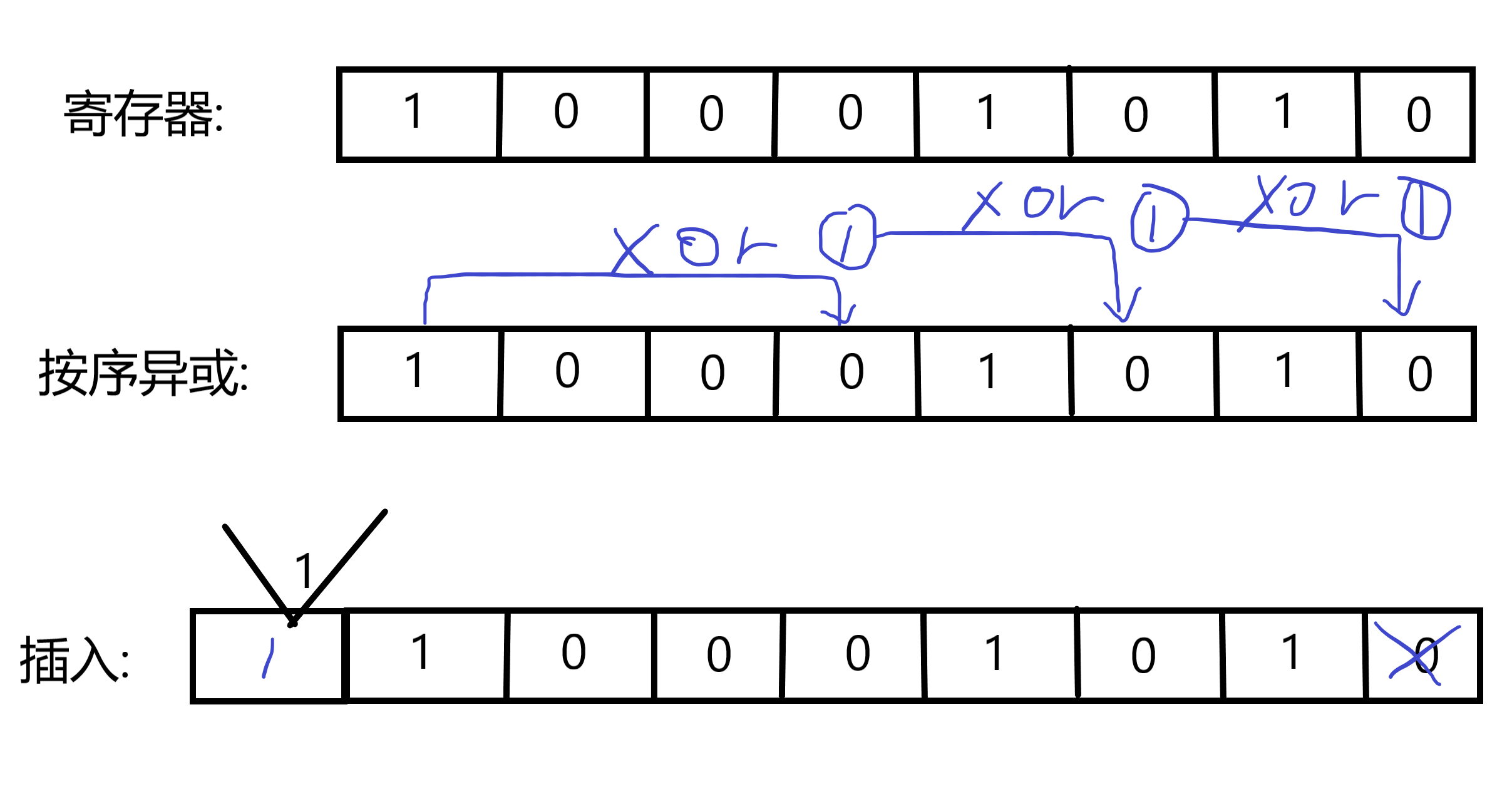
算法需要借助线性反馈移位寄存器(LFSR)生成随机数，主要使用的运算符是异或(xor)，我们采用8位寄存器的形式演示，初始化寄存器位10001010，然后定义反馈函数为：
$$
x^8+x^4+x^2+1
$$
所以我们根据x的重数可知，只需对第8、4、2、1按顺序做一次异或即可。然后丢掉最后一位，把当前结果插入首端。然后循环这个过程多次，就得到了随机序列。这便是旋转的过程。

我们使用C++实现这个过程。

#include <iostream>
#include <vector>

using namespace std;

// 十进制转二进制
vector<int> DextoBin(int num) {
    vector<int> bincode;
    while(num!=0){
        bincode.push_back(num % 2);
        num /= 2;
    }
    return bincode;
}
// 二进制转十进制
int BintoDex(vector<int> arr) {
    int dex = 0;
    for (int n = 0; n < arr.size(); n++) {
        int t = arr.size() - n - 1;
        dex += (arr[n] << t);
    }
    return dex;
}
// 移位
vector<int> moveBack(vector<int>& arr,int num) {
    for (vector<int>::iterator it = arr.begin()+1; it != arr.end();it++) {
        *it -= 1;
    }
    arr[0] = num;
    return arr;
}

// 生成MT数
int MT_random(int num) {
    int m = 0;
    int p = 0;
    vector<int> bin = DextoBin(num);
    if (bin.size() % 2 == 1) bin.push_back(0);
    // 取得反馈函数的最高次
    while ((bin.size() - (2 << m-1)) > bin.size() - (2 << m)) m++;
    for (; m == 1; m /= 4) p = bin[m] ^ bin[m >> 2];
    vector<int> res = moveBack(bin,p);
    return BintoDex(res);
}

int main()
{
    // 设置循环次数
    int time = 10;
    while (time > 1) cout<< MT_random(123) <<endl;
}