关于我在填报志愿时使用的妙法
收集数据
要知道要想分析,首先应该有数据,你可以在百度或者其他搜索引擎上搜索到高考相关信息,非常便捷,一般在填报志愿时一本分数线都会知道,不知道也没关系,无非是少了一份数据。
这里我以黑龙江5年内一本分数线举例,我们先定义出我们的数组:
1 | |
绘制图像
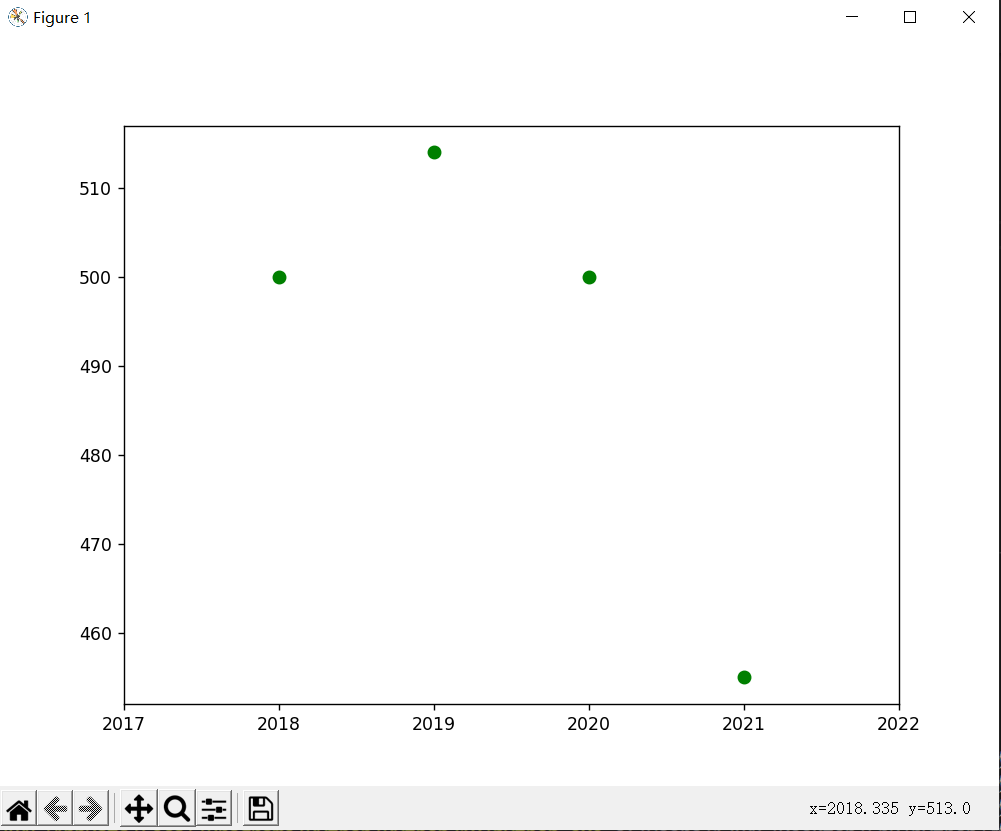
收集完分数后我们先绘制一下学校录取线关于年份的散点图:
1 | |
我们看到散点的走势先增后减,所以我们要用二次函数去拟合它,我们选择使用最小二乘法求参数,所以我们先抽象出函数的形式。
抽象函数我们需要使用一个能直接返回函数值的python函数和计算参数的函数
1 | |
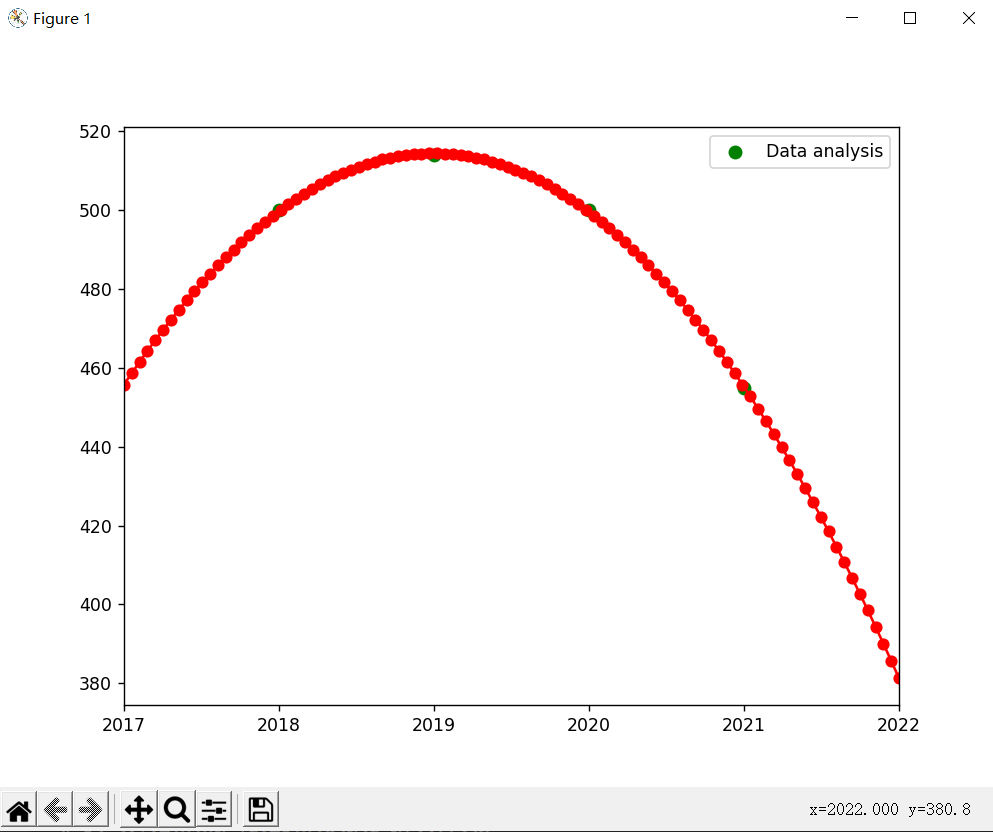
然后我们在main函数内加入二次函数,绘制出拟合曲线:
1 | |
我们看一下拟合曲线可以发现,拟合效果非常好,可以我们看到右下角我们要预测的值很离谱,只有380.8是不是意味着我们稳了呢?并不是,其实是我们在计算拟合曲线出错了,原因很简单,我们没有加入所有影响数据的变量,最重要的就是变量line,因为它的波动直接影响了拟合曲线,所以我们要使用的纵轴值应该时score-line。
结论与源码
最后我们把成品代码发一下,绘制出差值拟合图,最后我们得到学校和一本线的差距是多少
1 | |
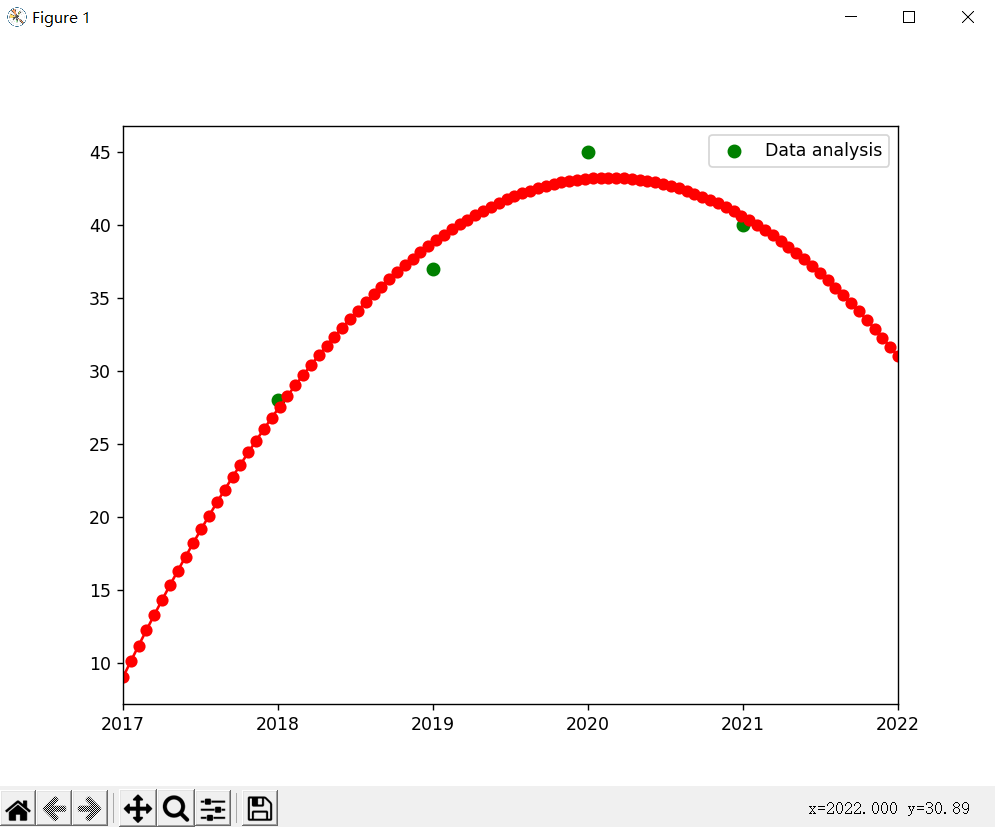
差值为30.89,如果预测了当年的一本线可以进行加和,如果已知那就更好了,我们是429分,我们对30.89进行四舍五入就是31,加和为460分。
据私下咨询招生办了解,当年的分数线是461分,误差很小了
总结
大数据的角度,数据之间都是有规律的,但正因为有人去发现与研究,这项技术才越发的实用,在这里预祝后来者们都能考上自己喜欢的大学,被喜欢的专业录取!
关于我在填报志愿时使用的妙法
https://blog.minloha.cn/posts/182513d7b677dc2022072519.html