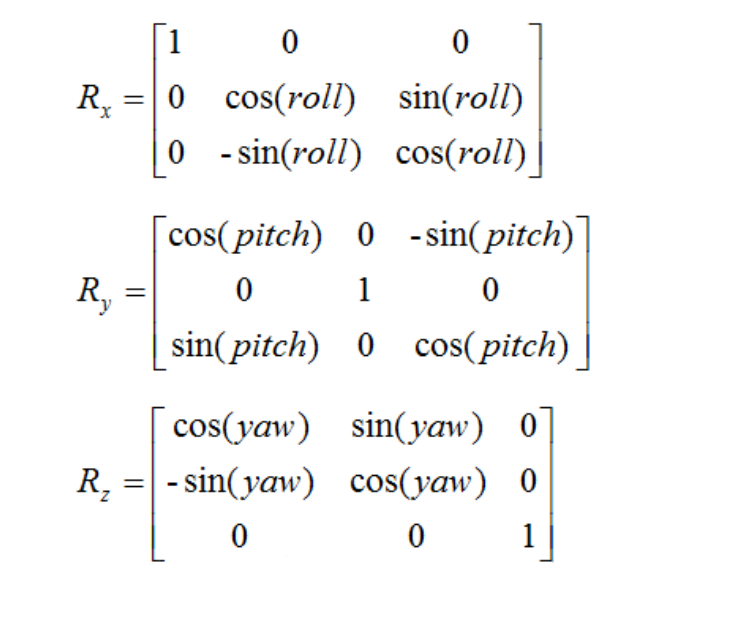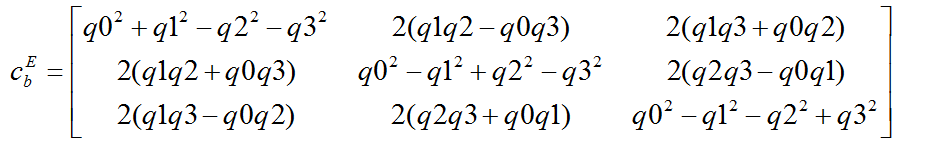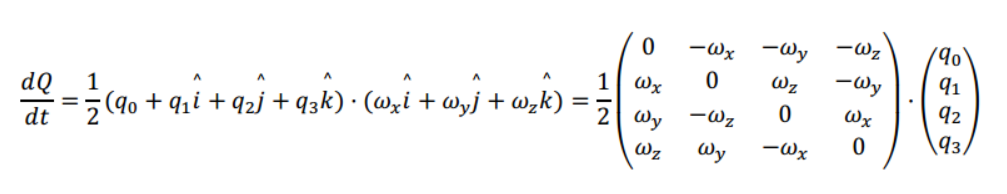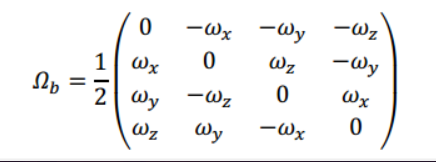写一个四旋翼的飞控吧

材料

无人机部分

飞控开发板：STM32F411CEU6 31.9元

无刷电机：2204-2300KV 正、反齿各两个 24.8 × 4元

电调：新西达30A（无校准） 30 * 4元

机架及尺寸：XL7碳纤维，臂长7英寸 129元

螺旋桨：APC 6*4 正反桨 8 × 2 + 9

陀螺仪：MPU6050 7元

通信模块：NRF24L01天线1100米 10.4元

电压模块：INA226 18元

气压计：GY-63 30元

3S电池：2200mAh + 2800mAh 62+54.9元

控制部分

控制芯片：STM32F103C8T6 17元

通信模块：NRF24L01天线1100米 10.4元

串口模块：USB—TTL

关键技术

关键技术主要是控制无人机的稳定飞行，至于pwm驱动电调就不做探讨，因为相对比较简单。

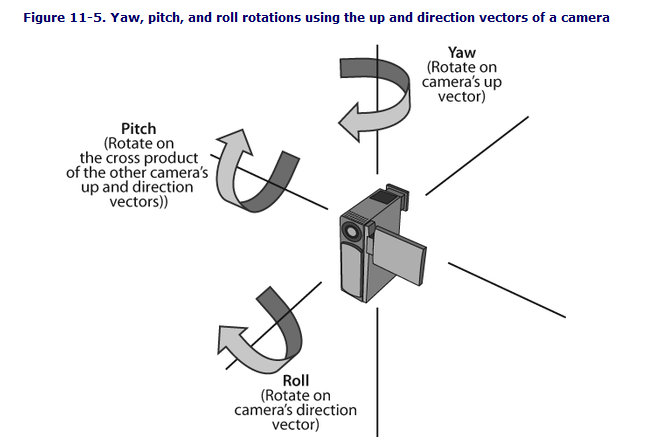
姿态解算

四元数法

欧拉角与四元数

表达姿态一般通过欧拉角表示，分为俯仰角(Pitch)、横滚角(Roll)、偏航角(Yaw)，旋转某一个角可以用一个旋转矩阵表示，他们可以用e的单位阵次幂进行泰勒展开逼近角度。

1

他们对应的三个旋转矩阵为：

2

我们把三个矩阵乘到一起，就可以用一个矩阵表达一个连续的变化了。这里要注意，因为矩阵没有交换律，所以先后顺序对最终结果的影响很大。

做无人机时经常会听到一个词汇叫“万向锁”，它的起因是当无人机的俯仰到垂直方向的时候，无法判断是俯仰还是横滚，所以造成了表征不明显，聪明的人们想到了在复坐标系表达姿态，这里面用到了超复数（一种双曲复数）的和，三个复数分别为i、j、k，他们有这样的关系：
$$
i^2=j^2=k^2=-1
$$
以及交换变号的性质：
$$
ij=k → ji=-k
$$

$$
jk=i→kj=-i
$$

$$
ki=j→ik=-j
$$

最后我们在每一个复数单位前增加一个系数，最后增加一个常数，就得到了四元数：
$$
Q=q_0+q_1i+q_2j+q_3k
$$
其中它的二范数只计算系数。关于计算的性质可以阅读下面链接的内容。同时我们的复数还可以表达一次90度的旋转，所以我们有了用四元数表达旋转的方法。当然，既然是复数就可以用欧拉公式变成三角值。

https://www.zhihu.com/tardis/bd/art/97186723

旋转矩阵

综上所述，我们得到了一种用四元数表达角度的方法，接下来我们看看如何求解角速度：

龙格库塔更新四元数

这个过程我们主要是求解$\frac{dQ}{dt}$，所以我们需要表达一下：
$$
\frac{dQ}{dt}=\frac{1}{2}sin(\frac{\theta}{2})\frac{d\theta}{dt}+\vec C sin(\frac{\theta}{2})\frac{d\theta}{dt} + \frac{d\vec C}{dt}sin(\frac{\theta}{2})
$$
其中的C为三个复数组成的向量，导数等于0，平方等于-1。$\theta$为四元数利用欧拉公式计算的角度，我们将其转化为角速度就得到：
$$
\frac{dQ}{dt}=\frac{1}{2}\vec C \omega(cos(\frac{\theta}{2}) + \vec C sin(\frac{\theta}{2}))=\frac{1}{2}\omega Q
$$
最后化简得到：

4

当然可以简单写作：
$$
\frac{dQ}{dt}=\Omega_bQ
$$
其中：

5

更新四元数的方法为：
$$
Q_{t+\Delta t}=Q_t+\frac{\Delta t}{2}\Omega_bQ_t
$$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
// 四元数
typedef struct {
    double q0;
    double q1;
    double q2;
    double q3;
} Quaternion_t;

// 姿态传感器数据
typedef struct {
	// 角度
    int16_t Accel_X_RAW;
    int16_t Accel_Y_RAW;
    int16_t Accel_Z_RAW;
    double Ax;
    double Ay;
    double Az;

    // 角速度
    int16_t Gyro_X_RAW;
    int16_t Gyro_Y_RAW;
    int16_t Gyro_Z_RAW;
    double Gx;
    double Gy;
    double Gz;

    // 温度
    float Temperature;

    //卡尔曼滤波后的角度
    double KalmanAngleX;
    double KalmanAngleY;
    double KalmanAngleZ;

    // 原始角度
    double NormalAngleX;
    double NormalAngleY;
    double NormalAngleZ;
} MPU6050_t;

void Quaternion_fromAxisAngle(Quaternion_t *Quat, MPU6050_t *data){
    double cosRoll = cos(data->KalmanAngleX / 2.0);
    double sinRoll = sin(data->KalmanAngleX / 2.0);
    double cosPitch = cos(data->KalmanAngleY / 2.0);
    double sinPitch = sin(data->KalmanAngleY / 2.0);
    double cosYaw = cos(data->NormalAngleZ / 2.0);
    double sinYaw = sin(data->NormalAngleZ / 2.0);
    Quat->q0 = cosRoll * cosPitch * cosYaw + sinRoll * sinPitch * sinYaw;
    Quat->q1 = sinRoll * cosPitch * cosYaw - cosRoll * sinPitch * sinYaw;
    Quat->q2 = cosRoll * sinPitch * cosYaw + sinRoll * cosPitch * sinYaw;
    Quat->q3 = cosRoll * cosPitch * sinYaw - sinRoll * sinPitch * cosYaw;
}

// 龙格库塔更新
void Quaternion_fromAngularVelocity(Quaternion_t *Quat, MPU6050_t *data, double dt){
    double p = data->Gx;
    double q = data->Gy;
    double r = data->Gz;
    Quat->q0 += dt * (0.5 * (-q * Quat->q1 - r * Quat->q2) - 0.5 * (Quat->q0 * p + Quat->q1 * q + Quat->q2 * r));
    Quat->q1 += dt * (0.5 * (p * Quat->q0 + r * Quat->q3) - 0.5 * (q * Quat->q0 + Quat->q2 * p + Quat->q3 * r));
    Quat->q2 += dt * (0.5 * (q * Quat->q3 - r * Quat->q0) - 0.5 * (Quat->q0 * r + Quat->q1 * p + Quat->q3 * p));
    Quat->q3 += dt * (0.5 * (q * Quat->q2 + r * Quat->q1) - 0.5 * (Quat->q0 * q + Quat->q1 * r + Quat->q2 * p));
}

卡尔曼法

在我的代码中使用到的就是卡尔曼滤波法。此法难度不大，但是过程较长，缺点是因为没有磁力计无法直接获取yaw值。如果对卡尔曼滤波公式不了解的可以阅读我的往期博客：卡尔曼滤波https://blog.minloha.cn/2023/02/16/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2/

公式：

$$
1):\hat x_i^-=F\hat x_{i-1}+Bu_{i-1}
$$

$$
2):P_i^-=FP_{i-1}F^T+Q
$$

$$
3):K_i=P_i^-H^T(HP_i^-H^T+R)^{-1}
$$

$$
4):\hat x_i=\hat x_i^-+K_i(y_i-H\hat x_i^-)
$$

$$
5):P_i=(E-K_iH)P_i^-
$$

公式转换为代码可以阅读下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
typedef struct {
    double Q_angle; // 噪声协方差
    double Q_bias; // 噪声偏差
    double R_measure; // 随机噪声
    double angle;
    double bias;
    double P[2][2];
} Kalman_t;


double Kalman_getAngle(Kalman_t *Kalman, double newAngle, double newRate, double dt) {
    // 公式1
    double rate = newRate - Kalman->bias;
    Kalman->angle += dt * rate;

    // 公式2
    Kalman->P[0][0] += dt * (dt * Kalman->P[1][1] - Kalman->P[0][1] - Kalman->P[1][0] + Kalman->Q_angle);
    Kalman->P[0][1] -= dt * Kalman->P[1][1];
    Kalman->P[1][0] -= dt * Kalman->P[1][1];
    Kalman->P[1][1] += Kalman->Q_bias * dt;

    // 公式3
    double S = Kalman->P[0][0] + Kalman->R_measure;
    double K[2];
    K[0] = Kalman->P[0][0] / S;
    K[1] = Kalman->P[1][0] / S;

    // 公式4
    double y = newAngle - Kalman->angle;
    Kalman->angle += K[0] * y;
    Kalman->bias += K[1] * y;

    // 公式5
    double P00_temp = Kalman->P[0][0];
    double P01_temp = Kalman->P[0][1];

    Kalman->P[0][0] -= K[0] * P00_temp;
    Kalman->P[0][1] -= K[0] * P01_temp;
    Kalman->P[1][0] -= K[1] * P00_temp;
    Kalman->P[1][1] -= K[1] * P01_temp;
	// 结束，返回角度
    return Kalman->angle;
}

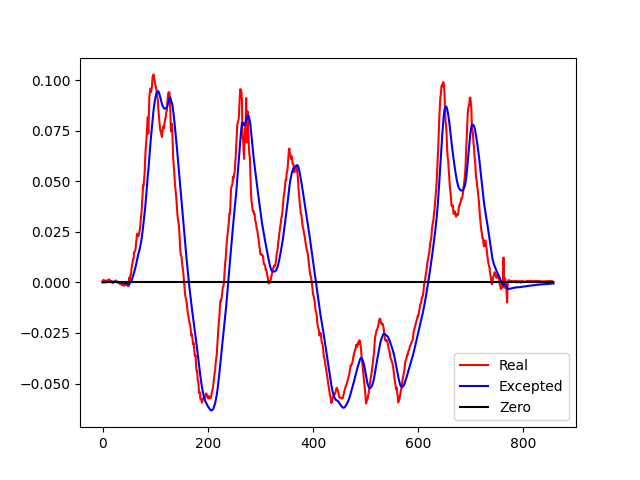
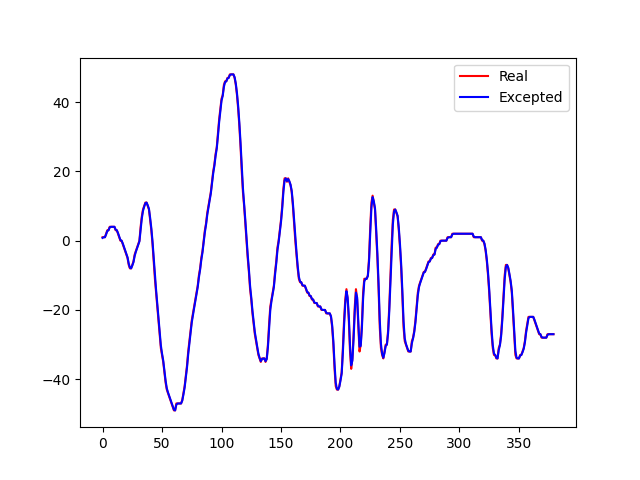
对于卡尔曼调参，这里给出一段python算法，只需要通过串口获取角度，保存到文件即可，然后使用下面的代码，让蓝色曲线更加平滑即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
import matplotlib.pyplot as plt
normal_degree = []
acc = []

with open('test.txt', 'r') as file:
    lines = file.readlines()
    for st in lines:
        sp = st.split(",")
        normal_degree.append(float(sp[0]))
        acc.append(float(sp[1]))


Q_angle = 0.2
Q_bias = 0.4
R_measure = 0.4
dt = 0.001


global angle
global bias
global P
global S
global K

def Kalman(newAngle, newRate, dt):
    global Q_angle
    global Q_bias
    global R_measure
    global angle
    global bias
    global P
    global S
    global K
    rate = newRate - bias
    angle += dt * rate
    P[0][0] += dt * (dt * P[1][1] - P[0][1] - P[1][0] + Q_angle)
    P[0][1] -= dt * P[1][1]
    P[1][0] -= dt * P[1][1]
    P[1][1] += Q_bias * dt
    S = P[0][0] + R_measure
    K[0] = P[0][0] / S
    K[1] = P[1][0] / S
    y = newAngle - angle
    angle += K[0] * y
    bias += K[1] * y
    P[0][0] -= K[0] * P[0][0]
    P[0][1] -= K[0] * P[0][1]
    P[1][0] -= K[1] * P[0][0]
    P[1][1] -= K[1] * P[0][1]
    return angle


if __name__ == "__main__":
    for i in range(len(normal_degree)):
        normal_degree[i] = float(normal_degree[i])
        pass
    angle = 0
    bias = 0
    P = [[0, 0], [0, 0]]
    S = 0
    K = [0, 0]
    list_ex = []
    list_x = []
    y = []
    lim = 20
    for i in range(lim):
        list_ex.append(Kalman(normal_degree[i], acc[i], dt))
        list_x.append(normal_degree[i])
        pass
    
    x = [i for i in range(lim)]
    y = [0 for i in range(lim)]
    plt.plot(x, list_x, color="red")
    plt.plot(x, list_ex, color="blue")
    plt.plot(x, y, color="black")
    plt.legend(['Real', 'Excepted','Zero'])
    plt.show()
    pass

效果展示图：

6

PID算法

提及控制算法，就不得不提到PID算法，这是一种闭环控制算法，输入参数只需要实际值和期望值即可，他共有两种格式：增量式和位置式
$$
位置式: o(k)=K_pe(k)+K_i\sum_{i=0}e(i)+K_d[e(k)-e(k-1)]
$$
其中e为实际值与期望值的差，Kp，Ki，Kd为手工调节的参数。
$$
增量式：\Delta o(k)=K_p[e(k)-e(k-1)]+K_ie(k)+K_d[e(k)-2e(k-1)+e(k-2)]
$$
一般都是使用位置式，相关代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
typedef struct{
    double P;
    double I;
    double D;
    double I_threshold;

    double Pout;
    double Iout;
    double Dout;

    double finnalOUT;
    double Error;
    double lastError;
    double integral;
} PID_t;

#define limit(value,max) if(value > max) value = max;

double PID_Run(PID_t *PID,double target,double measure){
    PID->Error = target - measure;
    PID->integral += PID->Error;

    PID->Pout = PID->P * PID->Error;
    PID->integral += PID->Error;
    PID->Iout = -PID->I * PID->integral;
    PID->Dout = PID->D * (PID->Error - PID->lastError);
    limit(PID->integral,PID->I_threshold);
    PID->lastError = PID->Error;
    PID->finnalOUT = PID->Pout + PID->Iout + PID->Dout;
    return PID->finnalOUT;
}

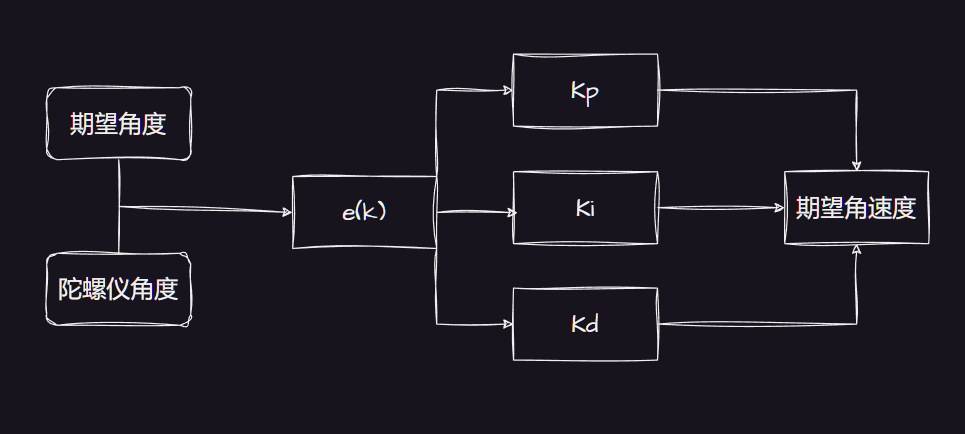
相关的流程图如下：

7

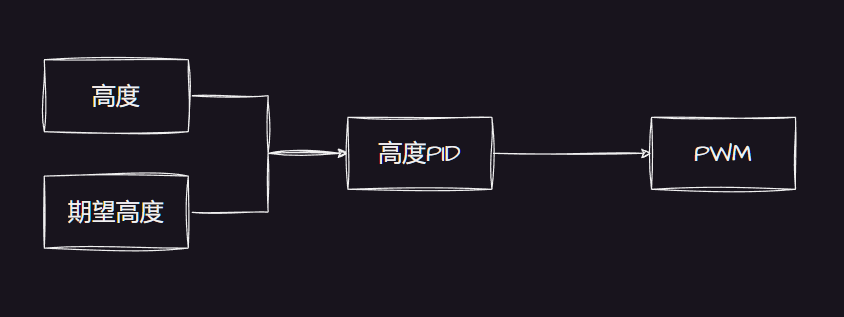
定高

我将定高放在PID后面是为了综合上面所有内容，这里我选择的获取高度的模块是气压计MS5611，他是IIC总线获取压强的模块，通过简单的计算就可以得到当前的高度。定高肯定需要有期望高度和实际高度，我们就可用PID控制输出的PWM。

8

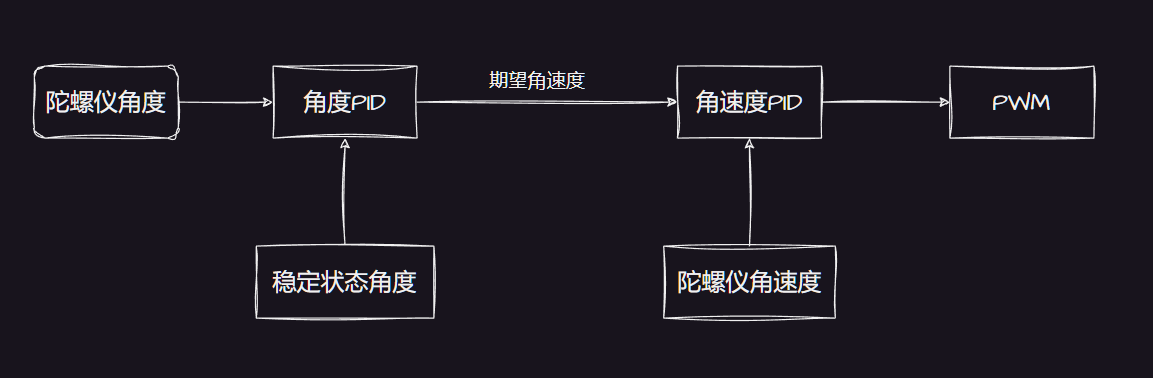
对于姿态稳定，我们可以用卡尔曼算法的姿态角计算角速度，然后计算PWM。也就是串级PID。

9

展示一下PID调参后的输出值。

10

总结

本次做一个四旋翼单纯只是玩一玩，展示一下图片后，本期博客就结束了。通过本文，读者可以清楚的了解四旋翼无人机的制作关键技术以及相关代码，读者可以自行采购物资进行设计一款自己的无人机。

11

技术
#C #嵌入式
写一个四旋翼的飞控吧
https://blog.minloha.cn/posts/2326184d4c18962023062628.html
作者
Minloha
发布于
2023年6月26日
更新于
2024年3月16日
许可协议