关于函数变换
复习变换
高中我们对函数的伸缩拉伸有所研究，在高中一般称呼为伸缩变换，但当我们观察变化后的坐标系和原来的坐标系，经过对比可以明显发现，坐标系发生了变化，我们可以通过一个三角函数的例子演示一下：
$$
y=sinx
$$
$$
y’=sin2x’
$$
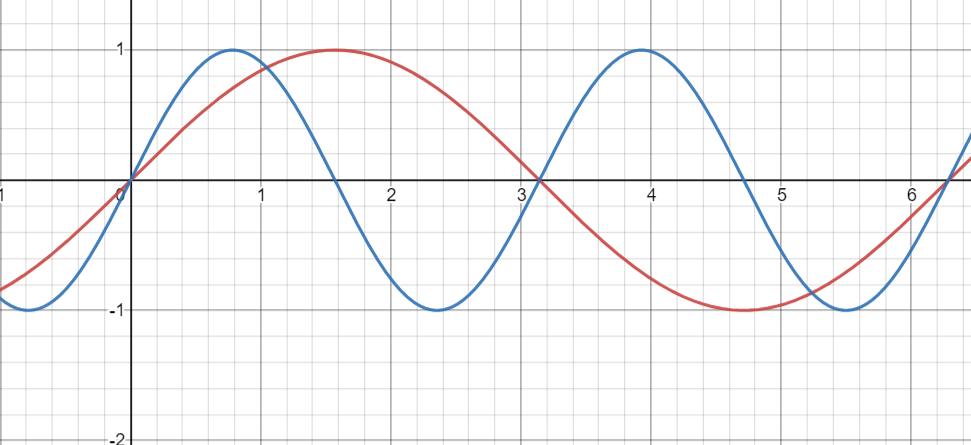
我们把变换后的函数换一种表示形式，即y'与y,x'与x的关系写出：
$$
\begin{cases}
x’=2x\
y’=y\
\end{cases}
$$
我们知道平面直角坐标系是Oxy，现在的坐标系是Ox'y'，从变化规则可以看出是对原Oxy坐标系的横轴x拉长2倍得到了新坐标系，而图像不变保持原来的位置，然后对齐新旧坐标系，就实现了图像的压缩。
同理我们也可以实现拉伸变换，还是使用正弦函数，我们做一下拉伸平移：
$$
y=sinx
$$
$$
y’=2sin(2x’+\pi)+2
$$
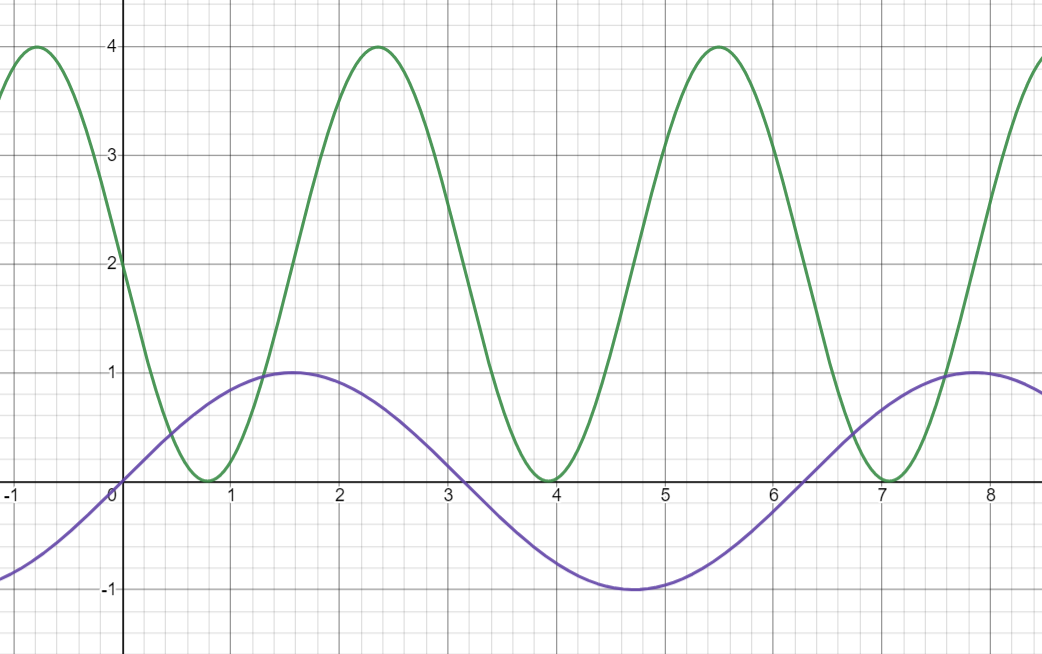
我们可以直观的看到，函数像弹簧一样被压缩，被拉伸，被平移，且我们可以写出变换规则：
$$
\begin{cases}
x’=\frac{1}{2}{(x-\pi)}\
y’=2y+2\
\end{cases}
$$
变化后的坐标系Ox'y'就是相对原Oxy坐标系的仿射
下定义
对于函数f(x,y)它的图形完全在由任意一组向量的张成空间内，规定这组向量组成的仿射系为L并绘制f(x,y)，通过对L进行变换基操作，得到的L’坐标系同时放入f(x,y)在L系内的图形，则f(x,y)在L’坐标系的内解析式$f_T(x,y)$叫做f(x,y)的变换。
切记切记，是原图像在新坐标系放入后，把新坐标系与原坐标系对齐后得到的函数叫做函数的变换函数！
算符演算的标准定义：
使问题从一种状态变化为另一种状态的手段称为操作符或算符。算符在单独存在时是没有什么意义。操作符可为走步、过程、规则、数学算子、运算符号或逻辑符号等。
所以我们的函数变换也是一种算符演算，当然你也可以理解为是在基本向量空间内的泛函分析。具体内容可以看实变函数与泛函分析。
对于标准的变换，我们可以通过变换函数实现，对于变换函数规定为下面形式：
$$
A=[\vec v_1,\vec v_2]\
$$
$$
条件:det(A)≠0\
$$
$$
f_T(x,y)=f(A[x,y]^T)\
$$
函数$f_T(x,y)$就是f(x,y)的变换后函数。A是线性算符
对于函数的变换，它是针对坐标系本身而不是针对函数，也就意味着无论如何变换，原坐标系的关系都不会改变，这里可以归纳为二组性质：
- 可逆性：存在f的反函数使得在L’内的图像可以重新回到原坐标系L内
- 相似性：原坐标系的关系，比如相切相交相离都不会改变
而对于函数的变换，我们可以用两种办法求出，也就是极坐标法或矩阵法，我列举一下优缺点
| 极坐标系 | 矩阵 | |
|---|---|---|
| 优点 | 是基础的内容便于理解，同时操作简单，前置基础要求不高，可以处理指定角度的旋转问题 | 可以直接表达出变换关系，极坐标法有的优点它都有，可以完成坐标系的定向拉伸，计算简单，理论知识完备。 |
| 缺点 | 无法处理伸缩问题，计算量大 | 需要线性代数的知识 |
| 特点 | 比较直观 | 可以处理任意坐标系 |
仿射与矩阵变换
我们都知道，对于任意两不共线向量的张成向量空间可以囊括整个二维平面的向量，而矩阵方程就是对这两个不共线向量（基）的操作，这里可以通过直观的例子感受一下，对于原坐标系，他的基向量是$\vec i$=(1,0)，纵$\vec j$=(0,1)，它们的列向量用矩阵表示就是：
$$
\left[\begin{matrix}
1&0\
0&1\
\end{matrix} \right]
$$
这种矩阵不是很熟悉吗？这个叫单位矩阵，任何向量或矩阵与它做外积都是本身，也就是坐标系并没有改变，而我们将他改为以(1,1)(1,-1)为基的向量空间时，我们就需要对原坐标系的向量做矩阵变换，即Ax=b,其中：
$$
A=\left[\begin{matrix}
1&1\
1&-1\
\end{matrix} \right]
$$
x就是自变向量，一般写作：
$$
\left[\begin{matrix}
x\
y\
\end{matrix} \right]或\left[\begin{matrix}
x&y\
\end{matrix} \right]^T
$$
b是变化后的向量，至于矩阵变化在之前说过，我给个传送门
https://blog.minloha.cn/2022/04/17/%E7%BB%86%E8%AF%B4%E7%9F%A9%E9%98%B5%E4%B8%8E%E5%8F%98%E6%8D%A2/
函数变换
函数变换这种知识其实并不存在，和矩阵方程一样，说出这个名词的（我）想表达函数变换其实是一个连续的过程。
首先我们先尝试一个二维空间内的二元函数：
$$
f(x,y)=\frac{x^2}{4}+y^2-1=0
$$
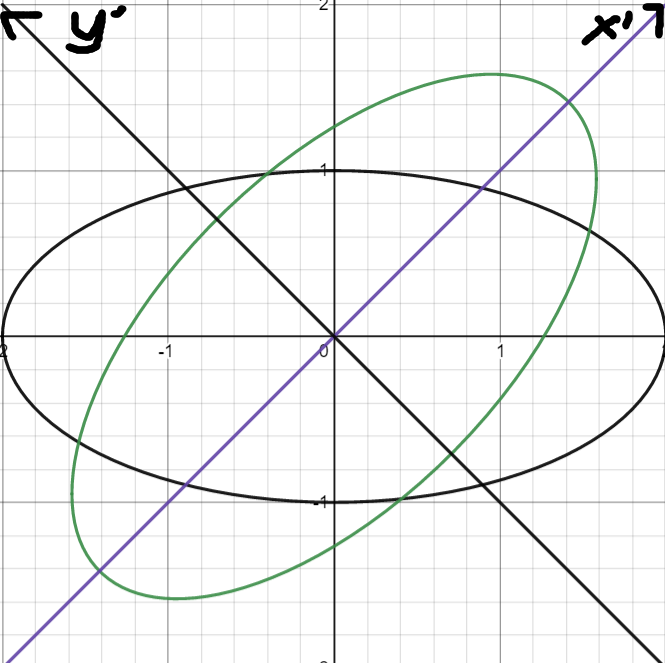
绘制他的图像，我们得到了一个椭圆，然后我们思考一下，如何在坐标系Oxy顺时针旋转45°得到椭圆
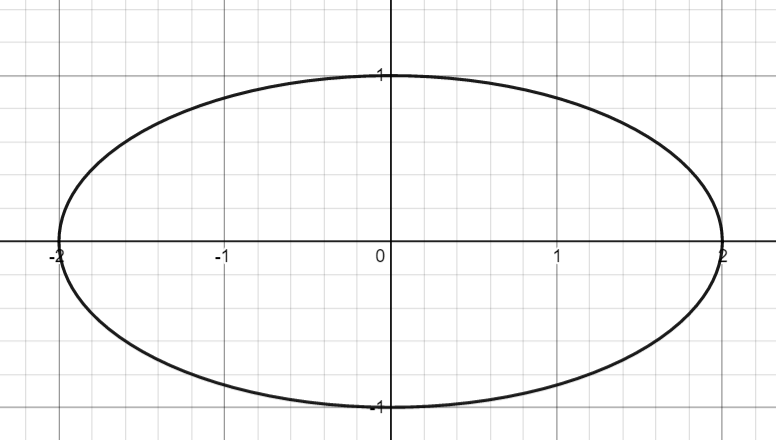
答案是极坐标方程，我们知道极坐标极径、极角和直角坐标的关系 x=ρcosθ，y=ρsinθ，且x²+y²=ρ²，而我们只需要给极角θ加上45°即可获得旋转方程，那么我们代入化简一下就可以得到旋转后的函数了：
$$
\frac{5}{8}x^{2}+\frac{3}{4}xy+\frac{5}{8}y^{2}=1
$$
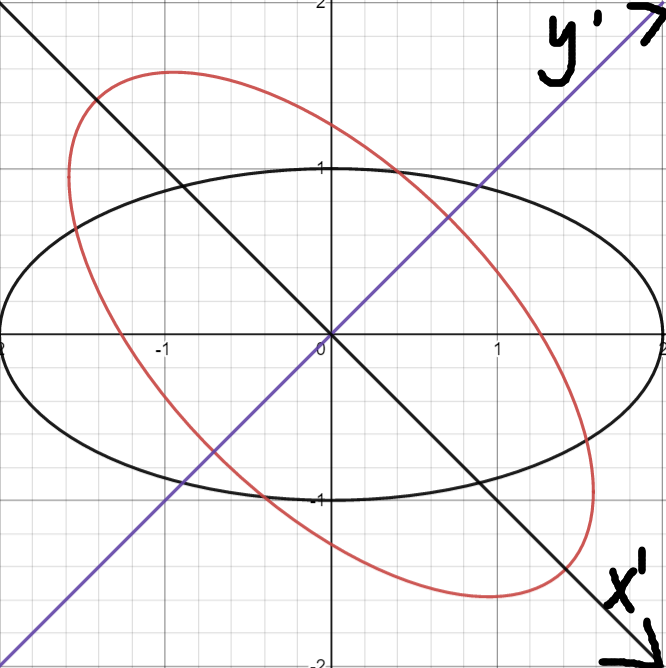
为了清楚看到变化后的坐标系，我绘制了Ox'y'坐标系，可以看出变化后的x'与原坐标系的x所成角度正好是45度。
那么我们总不能时刻都用极坐标系吧，不然这矩阵可就无处可施了，所以我们使用旋转矩阵R：
$$
R=\left[\begin{matrix}
cos \theta&sin\theta\
-sin \theta&cos\theta\
\end{matrix} \right]
$$
我们还是令θ=45°，椭圆上的点用列向量X=$[x，y]^T$（T为矩阵转置）表示，那么RX就是变化后的函数，我们通过矩阵外积计算一下结果可以轻松得到变化后的x'和y'关于原坐标x、y的方程，把x'和y'代会到解析式内，我们就可以计算出新函数了，它是这样的：
这里注意，矩阵是直接改变了坐标系，也就意味着是对坐标系本体发生了变换，如果想要完成换基，就需要用新基矩阵的逆去乘以变量向量。
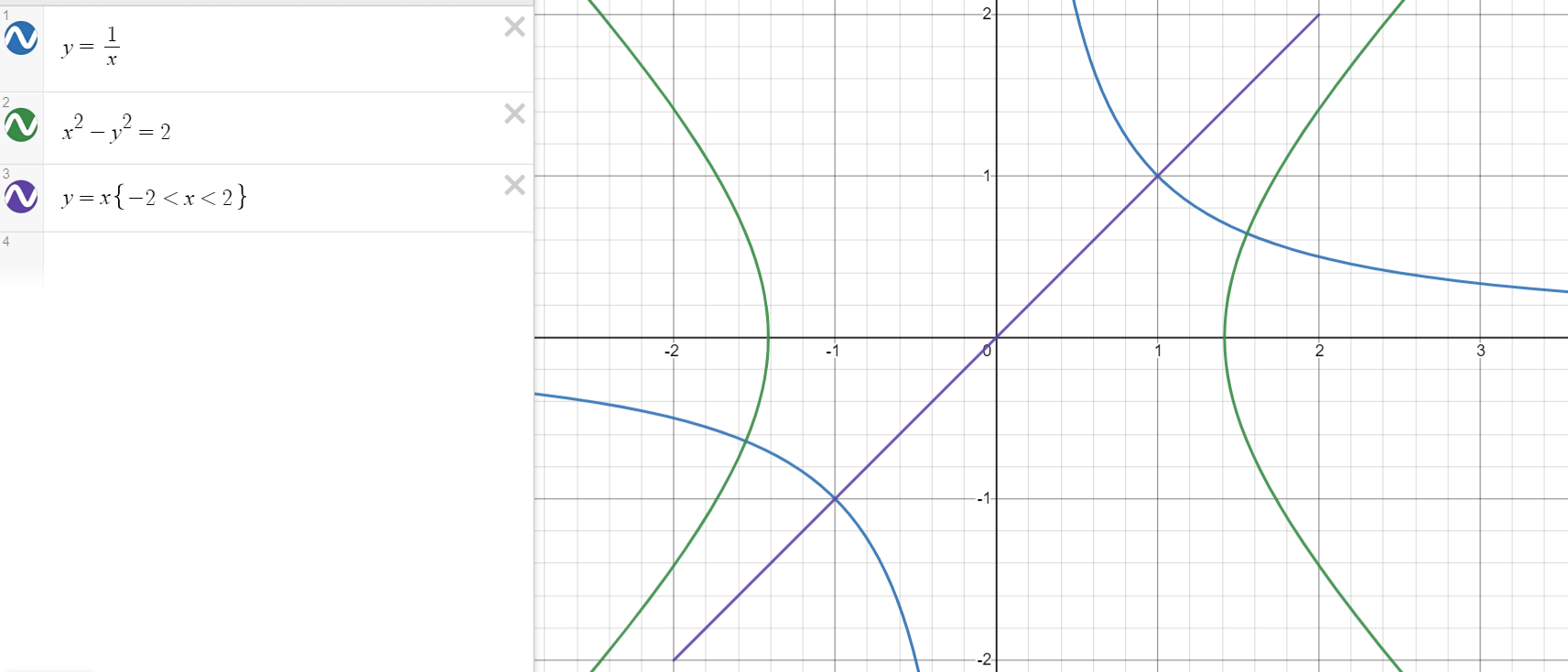
相似的，我们可以再用两种办法研究一下双曲线，也就是在初中学习的反比例函数：
$$
y=\frac{1}{x}
$$
我们对他进行化简，可以得到二元函数：
$$
f(x,y)=xy-1=0
$$
第一种极坐标法，我们还是让角度为45°，我简单列一下计算过程。
$$
\rho cos\theta*\rho sin\theta=1
$$
则可以计算θ’在参数方程的值，使用两角和打开正余弦，重新得到ρcosθ和ρsinθ
$$
\rho cos(\theta+\frac{\pi}{4})*\rho sin(\theta+\frac{\pi}{4})=1
$$
$$
(\rho sin\theta-\rho cos\theta)(\rho sin\theta+\rho cos\theta)=2
$$
即可推出：
$$
x^2-y^2=2
$$
然后再来尝试一下矩阵，定义变换函数为g(x,y)，满足下面矩阵，不过注意，这是旋转矩阵的逆哦！
$$
T=\left[\begin{matrix}
cos\frac{\pi}{4}&sin\frac{\pi}{4}\
sin\frac{\pi}{4}&-cos\frac{\pi}{4}\
\end{matrix} \right]
$$
$$
f_T(x,y)=f(T·\left[\begin{matrix}
x\
y\
\end{matrix} \right])
$$
我们乘一下，得到下面的内容：
$$
x’=\frac{\sqrt 2}{2}(x+y)\
$$
$$
y’=\frac{\sqrt 2}{2}(x-y)\
$$
我们把x'和y'带入进f(x,y)中，得到新的方程：
$$
x^2-y^2=2
$$
可以看到和我们使用极坐标是一样的。
高级玩法
我们让坐标系变成斜二测画法的坐标系，操作对象就选择椭圆了：
$$
\frac{x^2}{4}+y^2=1
$$
$$
T=\left[\begin{matrix}
1&\frac{1}{2}\
0&\frac{1}{2}\
\end{matrix} \right]
$$
那么就可以令f(x,y)是椭圆，求出它对应的变换函数了：
$$
f_T(x,y)=f(T·\left[\begin{matrix}
x\
y\
\end{matrix} \right])
$$
求解一下，得到变化后的方程已经图像如下：
$$
\frac{x^{2}}{4}+\frac{xy}{4}+\frac{5y^{2}}{16}=1
$$
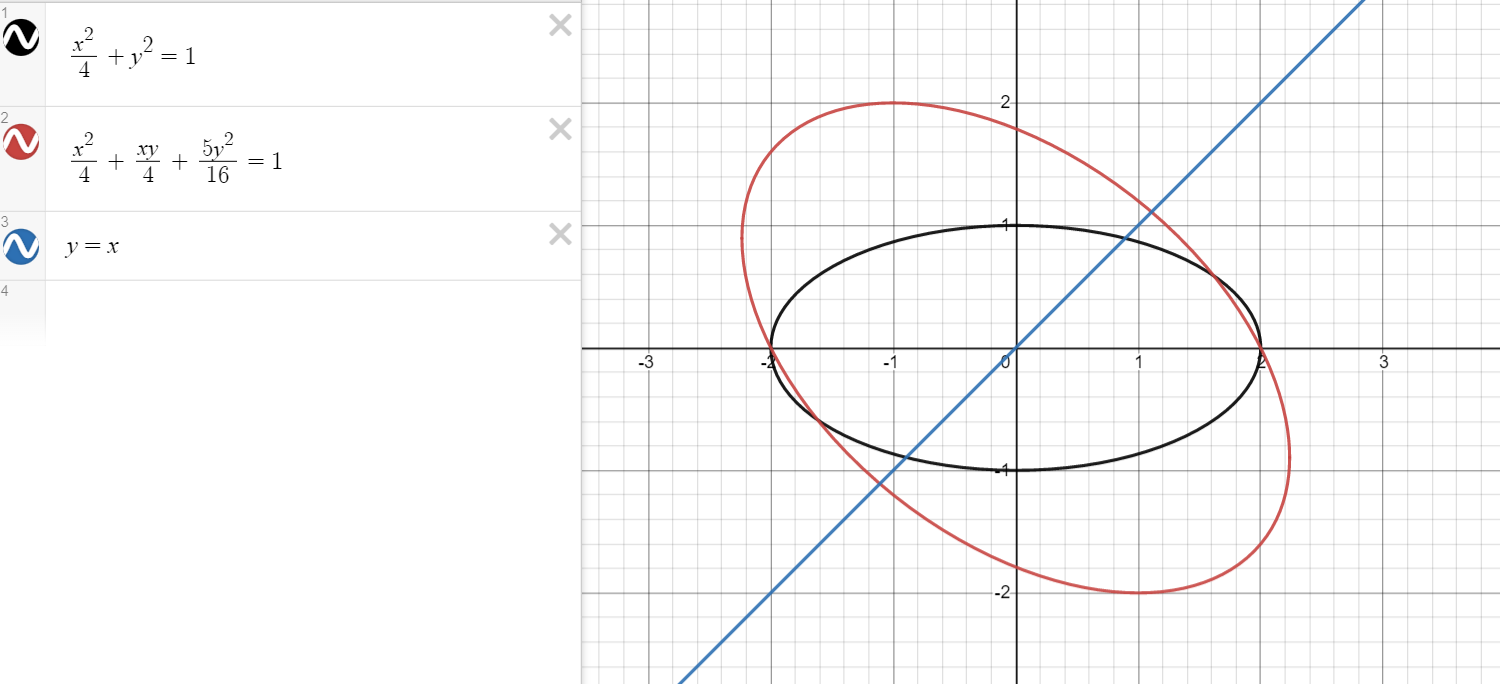
我们可以看出，矩阵变换可以完美解决伸缩坐标系的问题，至于y=x只是参考直线。
最后让我们看一个抛物线旋转的例子就结束吧！
$$
y^2=4x\
$$
$$
f(x,y)=\frac{y^2}{4x}-1=0(x≠0)\
$$
$$
T=\left[\begin{matrix}
cos\frac{\pi}{4}&sin\frac{\pi}{4}\
sin\frac{\pi}{4}&-cos\frac{\pi}{4}\
\end{matrix} \right]
$$
$$
f_T(x,y)=f(T·\left[\begin{matrix}
x\
y\
\end{matrix} \right])
$$
$$
f_T(x,y)=\frac{x^{2}}{2}-xy+\frac{y^{2}}{2}-2\sqrt{2}x-2\sqrt{2}y=0
$$
绘制图像：
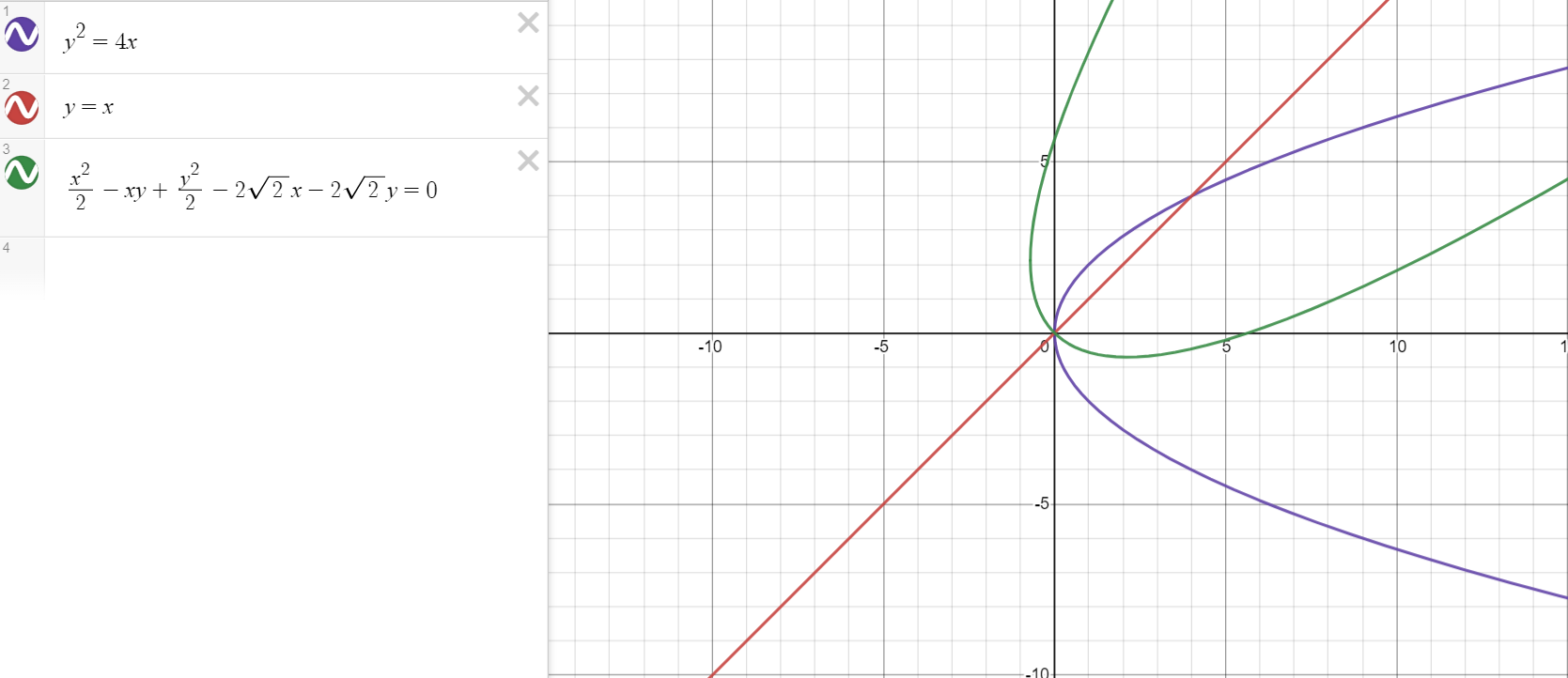
总结
这种圆锥曲线的旋转是我在做刷数学题时在压轴选择题看到的，刚开始并不太在意。现在学完高数多元函数之后对旋转有一个全新的认知，所以就简单尝试了一下关于函数变换也就是旋转平移仿射等操作，所以有了这篇博文，如果有任何问题都可以在下面留言，我都会回复的呢！记得收藏本站地址