学会神经网络[4]——图神经网络

图卷积神经网络

什么是图神经网络？这个是一个很有趣的概念，我们都知道图是一种表征能力极强的抽象数学对象，但是我们从未深度了解过图，我们仅知道图的组成元素和图的算法意义。那么在神经网络这里图一样可以发挥极大的作用，这里我们就用GCN进行最基本的视觉处理举例。

首先我们需要这些包。其中torch_geometric用于导入现成的图神经元，当然自己写难度也不大的

import torch
import torch.nn as nn
import torch.nn.functional as F
# torch_geometric是现成的图结构库，是在torch基础上开发的，当然有兴趣可以自己实现GCN
from torch_geometric.datasets import Planetoid
from torch_geometric.nn import GCNConv
from matplotlib import pyplot as plt

我们直接实现一下GCN的类，GCN即为图卷积神经网络，他需要提供输入数据x和边索引。

class GCN(nn.Module):
    def __init__(self, dataset=Planetoid(root='./data/', name='Cora')):
        super(GCN, self).__init__()
        self.conv1 = GCNConv(dataset.num_features, 16)
        self.conv2 = GCNConv(16, dataset.num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index
		
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)

对于GCNConv，最关键的参数就是输入变量和边的索引，我们通过多层堆叠矩阵的邻接矩阵，直接进行计算即可。最后我们实现训练算法。

def train(model, data, optimizer):
    model.train()
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

然后我们再实现测试精度算法。

def test(model, data):
    model.eval()
    out = model(data)
    pred = out.argmax(dim=1)
    test_correct = pred[data.test_mask] == data.y[data.test_mask]
    test_acc = int(test_correct.sum()) / int(data.test_mask.sum())
    return test_acc

最后我们实现main方法：

def main():
    model = GCN()
    model.to(device)
    dataset = Planetoid(root='./data/', name='Cora')
    data = dataset[0]
    data.to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
    acc_list = []

    for epoch in range(1, 100):
        train(model, data, optimizer)
        test_acc = test(model, data)
        acc_list.append(test_acc)
        print(f'Epoch: {epoch:03d}, Test: {test_acc:.4f}')
        pass

    plt.plot(acc_list)
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    plt.show()

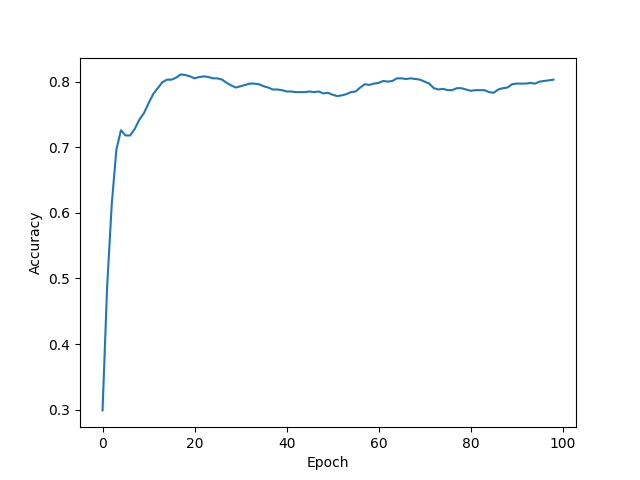
我们观察绘制出来的图像可以看到：

在有限步数内GCN趋于收敛，但是精度不太高。

---

看完了代码接下来说一说原理，这部分之后会单开一个文章讲讲图神经网络，这里先简单说说吧。

图神经网络通过邻居节点的表征和节点自身的表征完成更新，我们可以将图写作一整个邻接矩阵用于表示一个图，在图神经网络里面的图都是自环的，所以邻接矩阵的副对角线都是1。我们叫邻接矩阵为A，那么自环邻接矩阵为：

$$\hat A = A + I$$

假设每个节点的表征我们可以用一个向量表达，整个图的节点间存在权重，那么整个图就是一个非0的权重矩阵，我们叫他H。最开始的H等于输入X，那么我们可以把图神经网络的更新看作两步：

• 汇总：从各个节点的信息汇总到一起
• 聚合：将信息表征到新的节点上

对于我们的GCN也是一样的道理。GCN是在做卷积，傅里叶变换是特殊的拉普拉斯变换，所以我们求卷积可以求矩阵的拉普拉斯变换。下面给出传递公式：

$$H_i^k=\sigma(\hat D^{-\frac{1}{2}}\hat A \hat D^{-\frac{1}{2}}H^kW^k)$$

其中矩阵D也叫做角度矩阵，它的主对角线元素为A矩阵行的和，其他位置都是0，可以写作：

$$\hat D_{ii}=\sum_j\hat A_{ij}$$

更新节点数据也显得尤为重要，我们可以写作：

$$H_i^k=\sigma(\sum_{j∈{N(i)∪i}}\frac{\hat A_{ij}}{\sqrt{\hat D_{ii}\hat D_{ij}}}H_j^{k-1}W^k)$$

提出最后的i项可以得到：

$$H_i^k=\sigma(\sum_{j∈{N(i)}}\frac{\hat A_{ij}}{\sqrt{\hat D_{ii}\hat D_{ij}}}H_j^{k-1}W^k)+\frac{1}{\hat D_{i}}H_i^{k-1}W^k$$

这就是节点更新公式。那么我们为什么需要D这个奇怪的矩阵呢？很简单卷积就是傅里叶变换，而傅里叶是特殊的拉普拉斯，所以我们这个D就是起到拉普拉斯算子的近似值作用，接下来证明一下：

令傅里叶算子F：

$$F_\theta=diag(\theta)$$

数学上有：

$$F_\theta*x=UF_\theta U^Tx$$

其中U代表归一化的图拉普拉斯矩阵的特征线了矩阵，即：

$$L=I - D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$$ $$L=U\Lambda U^T$$

到此我们需要近似计算一下，众所周知，直接计算的代价很大（代码也会很大）所以我们需要使用切比雪夫多项式进行近似计算。

$$F_{\theta'}(\Lambda)=\sum_{k=0}^K\theta_{k}'T_k(\hat \Lambda)$$

其中的T就是k次展开切比雪夫多项式，我们重新写一下卷积得到：

$$F_\theta*x=\sum_{k=0}^K\theta_{k}'T_k(\hat L)x$$

---

其中的L为：

$$\hat L = \frac{2}{\lambda_{max}}L-I$$

我们可以看出每个节点只与K阶邻域内的节点信息有关。我们化简并最终得到：

$$F_\theta*x≈\theta(I+D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x$$

其中的D特征值很小，我们需要进一步稳定，所以我们需要给节点套上自环以确保不会梯度爆炸：

$$H=\hat D^{-\frac{1}{2}}\hat A \hat D^{-\frac{1}{2}}XW$$

其中的W是信息矩阵，X为输入信号。到此我们做出了充分的解释。图神经网络拥有较强的扩展性、可解释性和鲁棒性。所以才能受到如此青睐。

图注意力网络

图注意力网络英文缩写名为GAT，在刚才我们看到了GCN的效果其实并没有特别好，原因是我所使用的图卷积信息量太少了，所以我们需要在有限的信息量情况下提高精度。所以我们引入了注意力机制。

图注意力层定义了如何将第k-1层的隐藏节点表征更新到新的一层，可以写作一个简单的式子：

$$e_{ij}=a(WH_i^{k-1},WH_j^{k-1})$$

其中e表达节点间的关联强度，我们对强度计算SoftMax就得到了转移注意力的概率：

$$\alpha_{ij}=\frac{exp(e_{ij})}{\sum_{l∈N(i)}exp(e_{ij})}$$

这样我们每次转移前先乘注意力概率即可。接下来我们实现一下：

# 图注意力网络
class GAT(nn.Module):
    def __init__(self, num_node_features, num_classes):
        super(GAT, self).__init__()
        # 第一层注意力
        self.conv1 = pyg_nn.GATConv(num_node_features, 8, heads=8, dropout=0.6)
        # 第二层注意力
        self.conv2 = pyg_nn.GATConv(8 * 8, num_classes, heads=1, concat=False, dropout=0.6)

    def forward(self, x, edge_index):
        # 第一层注意力
        x = F.elu(self.conv1(x, edge_index))
        x = F.dropout(x, p=0.6, training=self.training)
        # 第二层注意力
        x = self.conv2(x, edge_index)
        return F.log_softmax(x, dim=1)

这里我用了一层图卷积作为关联强度计算的层。对于这种模糊对象用网络自己去拟合效果最好了。接下来直接放出训练方法和测试方法

def train(data, model, optimizer):
    model.train()
    optimizer.zero_grad()
    out = model(data.x, data.edge_index)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()
    return loss


def test(data, model):
    model.eval()
    out = model(data.x, data.edge_index)
    return accuracy(out[data.test_mask], data.y[data.test_mask])


def accuracy(out, y):
    pred = out.argmax(dim=1)
    correct = pred.eq(y)
    return correct.sum().item() / correct.size(0)

最后我们运用这些方法实现绘制精度曲线：

def main():
    # 数据集
    dataset = Planetoid(root='data', name='Cora')
    data = dataset[0]
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    data = data.to(device)

    # 模型dataset.num_node_features, dataset.num_classes这都没有
    model = GAT(num_node_features=dataset.num_features, num_classes=dataset.num_classes).to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=0.005, weight_decay=5e-4)

    # 训练
    acc = []
    for epoch in range(1, 100):
        loss = train(data, model, optimizer)
        test_acc = test(data, model)
        acc.append(test_acc)
        print(f'Epoch: {epoch:03d}, Loss: {loss:.4f}, Test Acc: {test_acc:.4f}')

    # 可视化精度曲线
    x = list(range(1, 100))
    plt.plot(x, acc)
    plt.xlabel('Epoch')
    plt.ylabel('Test Accuracy')
    plt.title('Test Accuracy of GAT')
    plt.show()

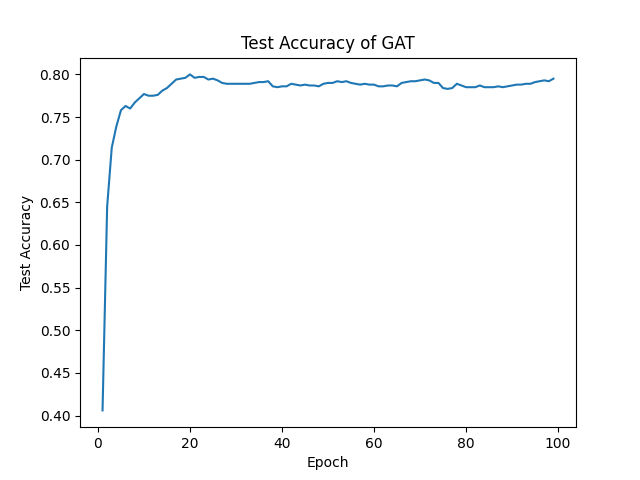
我们看一下运行效果：

根据对比我们发现增加了注意力之后学习速度更快了，这是极好的现象。