关于李理论的意义与SLAM应用
什么是李理论
在日常的线性代数中,我们用一个随性的矩阵就可以随意揉捏一个二维向量,包括:旋转,缩放,仿射等等,在平面系中。这些矩阵就可以实现各种各样的功能。但是如果衍生到高维度,矩阵就需要进行连乘,略显复杂。那么李理论的存在就是为了拓展其中的旋转。李理论的几何意义就是表达高维度的连续旋转。
那么在数学上,李理论是为了解决更高难度的微分方程提供的一套统一的理论,就像伽罗瓦求解代数方程的根一样。
在之前写一个无人机的时候我们表达一个旋转时用到了四元数的概念,一般小飞机都用四元数去表示,那么为什么四元数可以表达姿态呢?答案就是它是李理论的产物。李理论(Lie symmetry)包含了李群、李代数、李括号等等,这些理论都是在Sophus Lie死后才被发扬广大的。接下来就进入李理论的正题。
李理论各概念之间的关系
在维基百科中搜索李理论就会弹出一张图片(下图),要想理解这个图片首先需要知道群的概念:
- 群是群论研究的代数结构,群就是一种运算的集合,拥有各种性质。
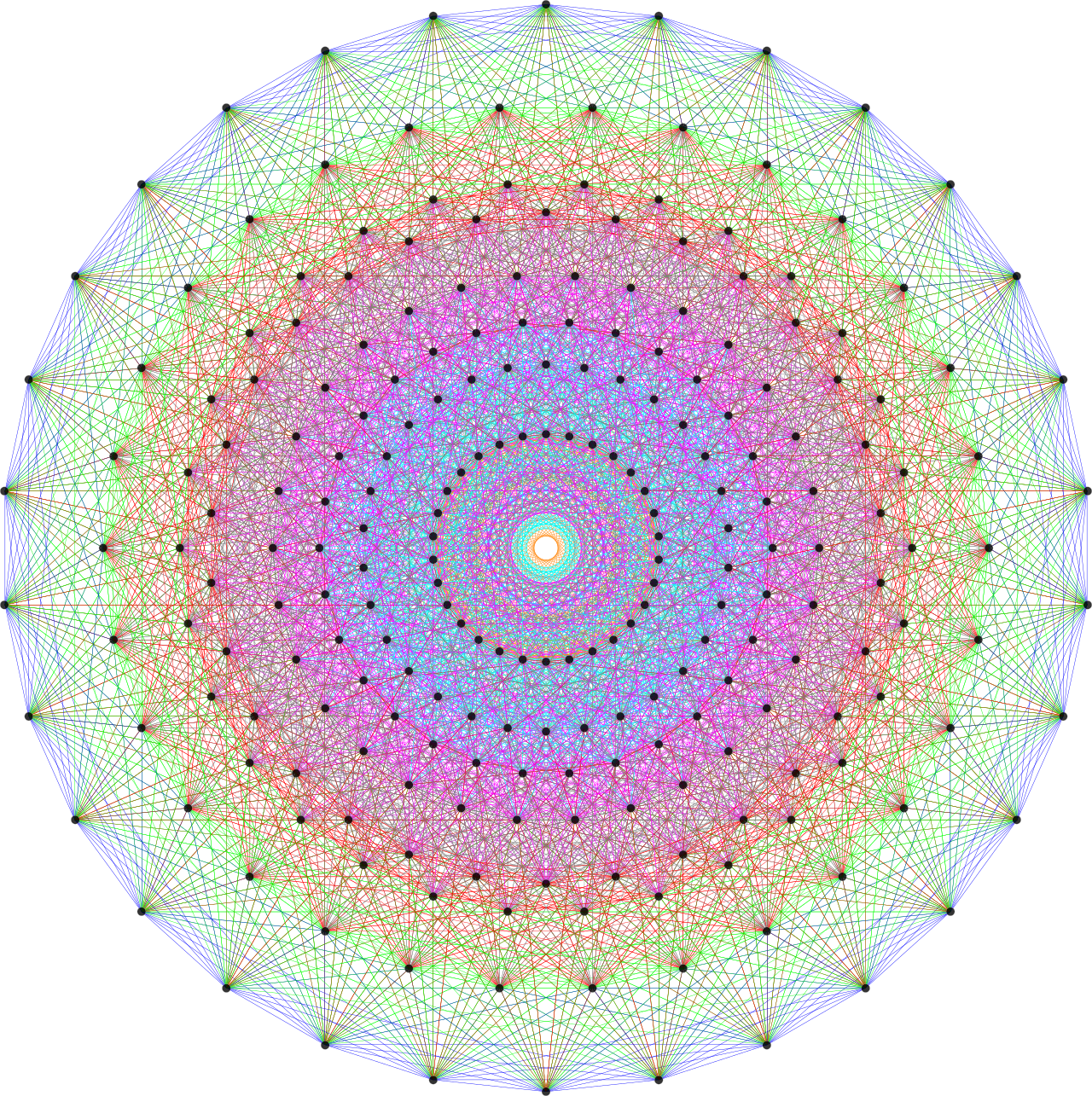
一个群可能是由各种更为简单的群组成的,如果一个群包含有限个元素,那他是有限群。那么有限群可以呗被分解成很多简单的群,这些群叫做简单群。简单群按照相似方式产生的群叫做无穷族。这张图叫做E8根系图,它是一组向量,可以通过它们的线性组合来构建整个代数的结构。根就是一组线性独立的向量(图这么画可能就是为了美吧)
李群它既是群还是流形,作为群而言它有封结幺逆。
- 封闭性:在群内的元素按照运算得到的元素仍在群内
- 结合性:比如g(h*f)=(g*h)f
- 幺元:e*g=g*e=g
- 逆元:g*h=h*g=e
而流形我们可以用一个圆举例,圆形被红色标记的部分就是一个流形。在圆中这个弧可以丝滑的变成直线,同样直线也可以丝滑的变成弧。
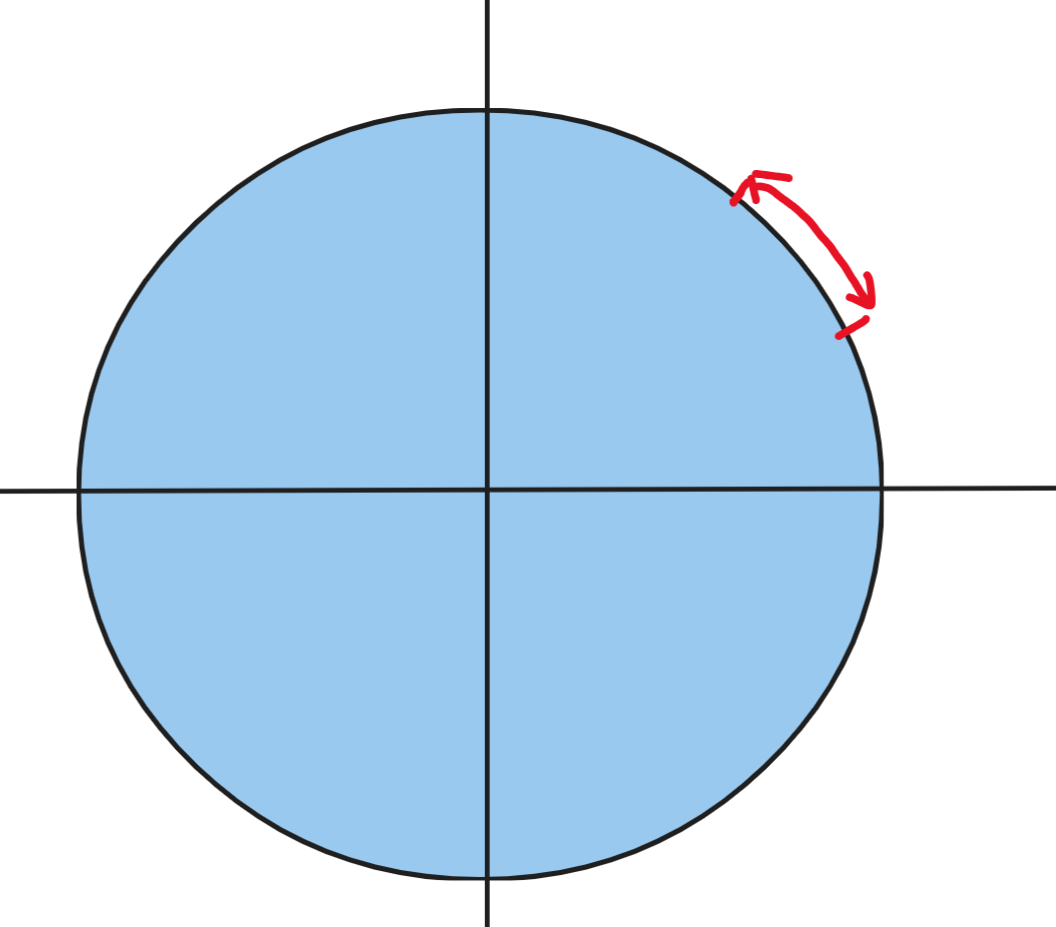
对于高维度的图形,比如三维的圆环形,任一个小平面也可以丝滑的从平面变成曲面,也可以从曲面变成平面。
用拓扑数学说,流形就是可以局部欧几里得空间化的一个拓扑空间,即在此拓扑空间中,每个点附近局部类似于欧氏空间。更精确地说,n维流形是一个拓扑空间,其性质是每个点都有一个邻域,该邻域同胚于n维欧氏空间的一个开集。通俗的说拓扑就是钢铁一样锻打图形,流形就是可以通过简单的压缩就能变化形状的图形。
李代数和李群有直接关系,我们举一个现实的例子:地球模型和地图的制作,古代人们都是通过一步一步测量测到的,相当于有了流形变成平面的过程,但是现代人们已经飞入太空,可以直观的观察地球全貌,地球需要将表面投影到一个平面上制成地图,这个地图就相当于李代数。
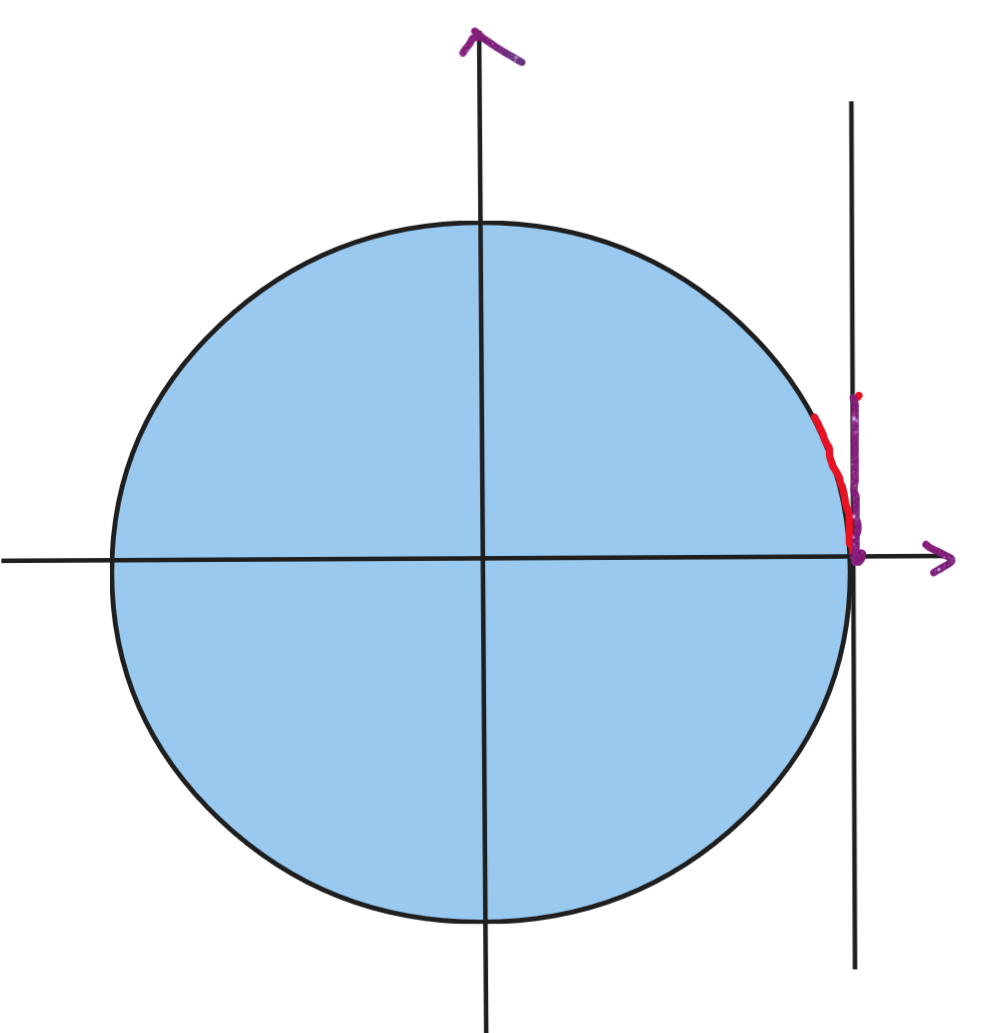
在复数域我们可以理解为一个映射过程:
当然,圆形上的一个点也可以理解一个向量。将它投影到平面就完成了李群映射到李代数。而在这个过程就是指数映射。而李代数就是李群的特殊空间,也叫切空间。
接下来我们把它升级到三维:
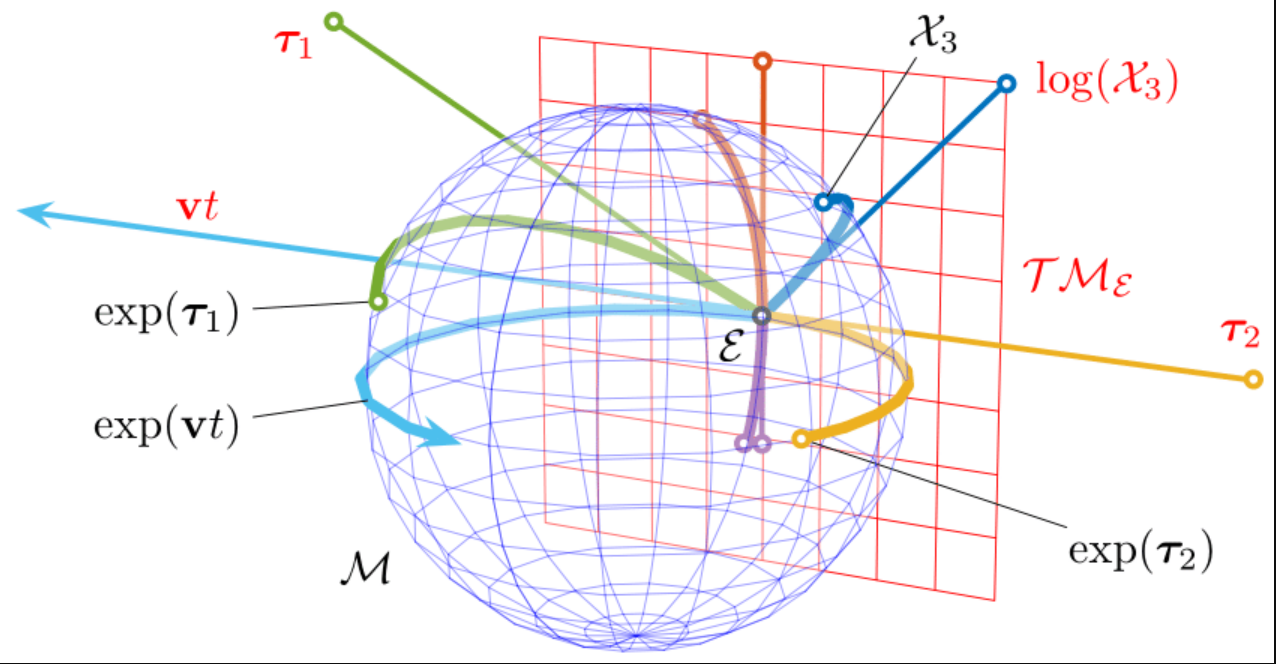
球面就是我们的李群,平面就是李代数。通过指数映射,李群中的每个元素在李代数中都有一个等价的元素 $X_3=exp(X_3)$,李代数上通过原点 $\epsilon$ 的每条直线在李群上都有一条等价的路径$vt=exp(vt)$这样的映射,使得在李群流形结构中的非线性运算 $\tau_i*\tau_j$ 在李代数线性空间中都有等价的线性运算。
我们发现李代数是对李群的局部描述,现在在球面上取几个点,并投影到平面上:
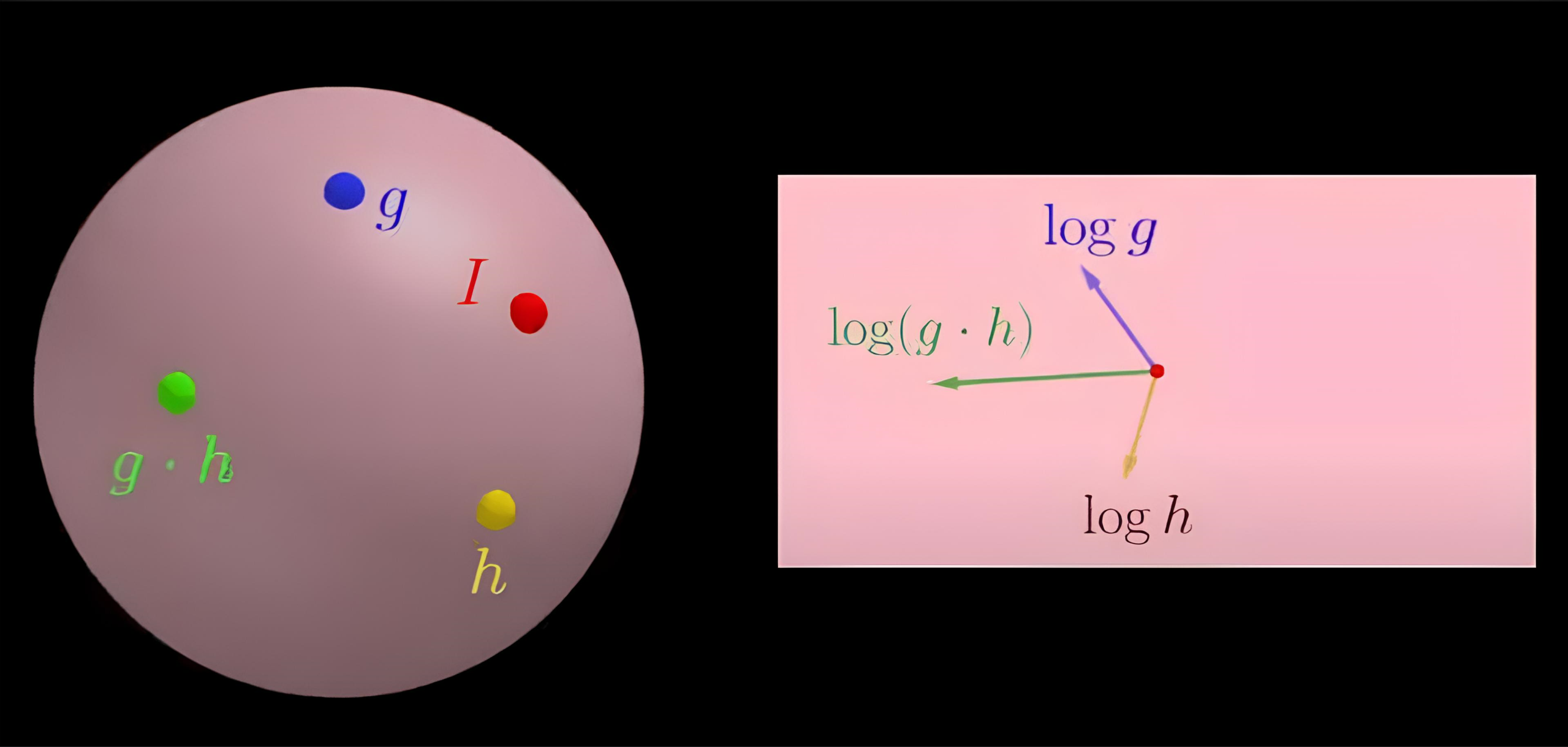
其中的gh为乘积,在三维空间这几个值都是向量所以我们可以做出大胆的猜测:
实际上我们可以用taylor展开得到:
而其中的[,]就是李括号,他的计算方式为:
简单缩写一下可以写作:$R=log(\vec g·\vec h)$,$A=log(\vec g)$,$B=log(\vec h)$,最终得到的这个公式叫做BCH公式,这样我们就可以在李代数上进行乘法。我们在两边在取指数就得到了逆变换,这就是李群和李代数沟通的桥梁:指数变换和对数变换。这样也联系了李群的加法和李代数的乘法
李群的性质
就在刚刚,我们完成了与李群、李代数和李括号的第一次见面,我们可以理解李括号为李群中的一种运算,他的存在就是沟通李群和李代数,对于复杂的Talyor展开计算过于麻烦。
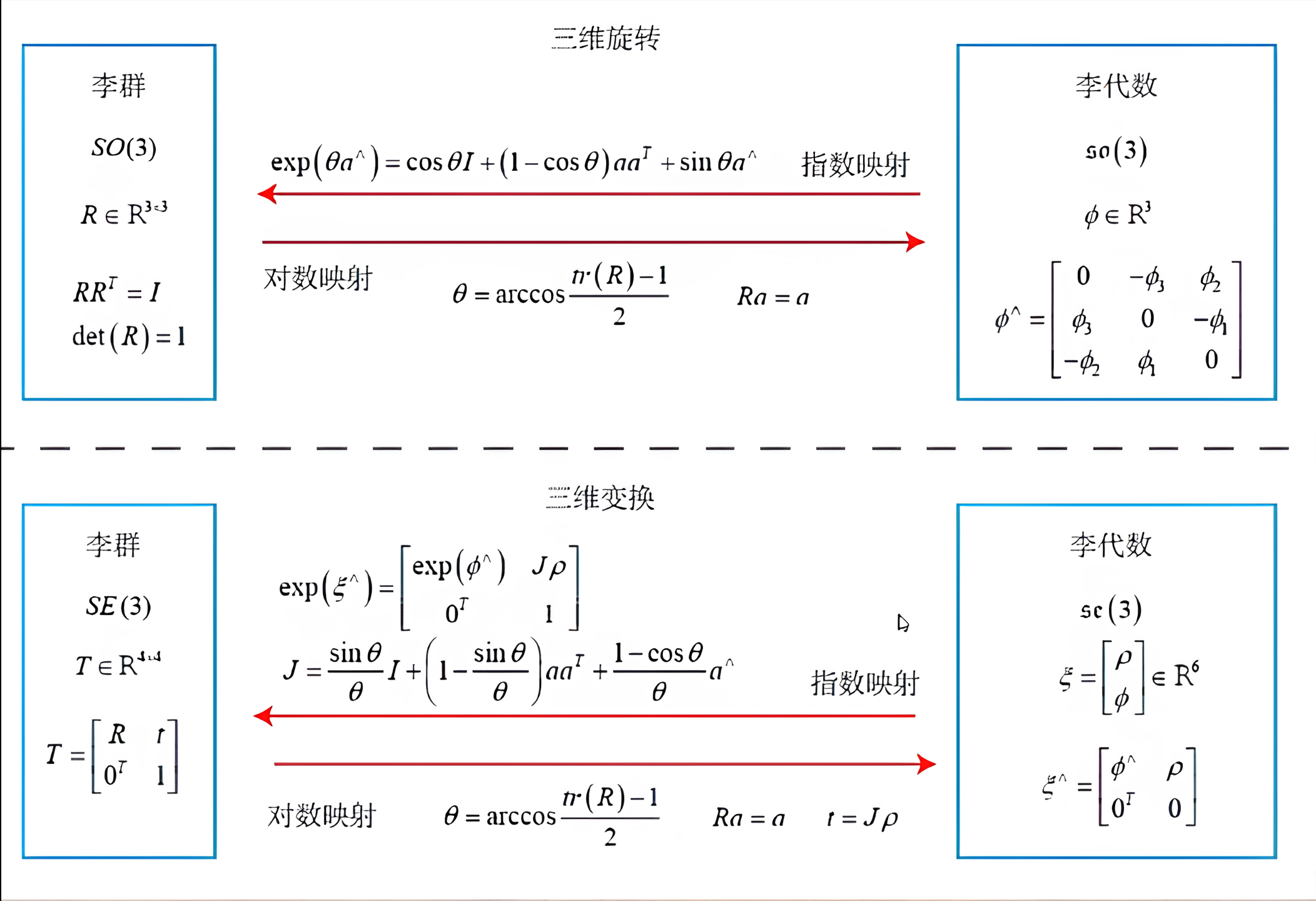
接下来定义两个特殊的SO3,SE3,so3,se3。其中大写的是李群,小写的是李代数
- SO3:三维空间旋转矩阵群
- SE3:三维特殊欧几里得群
补充几个数学中用到的群
- SU3:特殊幺正群,代表了复数三维空间上的幺正矩阵。
其中SO3包含现实含义:一个物体的连续三维运动,可以理解为一个旋转矩阵R关于时间t的函数,将其求导得:
移项得:
其中$R^TR’$满足反对称矩阵($A^T=-A$),记为:$\hat \omega$
我们经过简单计算得到:
对于一个微分量已经得到了一个确切的值。求解方程得到:
总结
最后总结就简单提一句,李理论可以应用在SLAM中,之后会写SLAM的文章,到时候也需要这些知识。