学会神经网络[1]——FNN与CNN

环境配置

安装python3.8：https://www.python.org/ftp/python/3.11.0/python-3.11.0-amd64.exe

安装N卡的CUDA和CUDNN：需要安装对应显卡版本，我这里是rtx 3070，所以安装对应版本即可

Pytorch：去官网选择CUDA版本，一定要选择显卡版本，cu后面的三位数字就是cuda版本号

测试环境：

import torch
print(torch.__version__)      # 配置正确应该输出cu版本号
print(torch.cuda.is_available()) # 配置正确应该输出true

基本叙述

首先，确保你掌握python语言的基础与基本的数学原理：

python基础部分在公众号就已经写过了，所以我就不抄了。

基本的原理可以看：https://blog.minloha.cn/posts/111300e57886172021121307.html

本系列博客的目的是帮助读者了解神经网络的实现原理与代码的写法，基础数学内容和python语法需要自行掌握。当然，涉及到了我就说一下哈~

全连接神经网络

所谓全连接神经网络自然就是基于MP神经元进行的网络结构，每层之间互不干涉，但是层与层之间每个节点都相互连接，同时也有前向传播（预测）和反向传播（学习），这些数学的运算公式可以在：神经网络的实现一期中看到，那么我们如何用pytorch实现这样的一个神经网络呢？

首先我们需要清楚全连接神经网络(FNN)是做什么的，我们可以把它理解为一种简单的函数拟合器，每次计算的过程输入是一个向量，输出也是一个向量。所以FNN姑且叫他向量计算器，那么最简单的就是线性回归计算（当然非线性也可以）

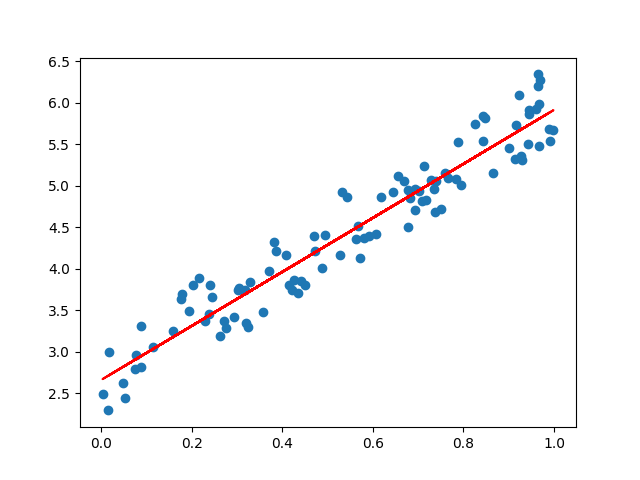
根据单层神经网络可以拟合任意单值连续函数，我们可以用一个线性数据生成器当作数据样本，一个单层神经网络就可以：

def generate_data():
    # 生成100个随机数, 1列
    x = torch.rand(100, 1)
    # 生成y = 3.3x + 2.2 + 一些噪声
    y = x * 3.3 + 2.2 + torch.rand(100, 1)
    return x, y

这里用到了函数torch.rand，两个参数分别为向量数和向量的秩。同时torch有加减乘除，直接用对应符号即可，对于矩阵点乘就可以用*，而外积得用@符号计算。

如何写一个神经网络？神经网络究竟是什么？

- 一般神经网络可以简单为一种万能函数拟合器，但是每种神经网络都有自己的拟合范围，比如CNN更擅长对矩阵操作，FNN更擅长对向量操作等等
- 当我们掌握一般神经网络结构后，我们可以把它究竟是哪一部分可以实现这种功能给分析出来，比如FNN为什么擅长对向量操作，原因就是他的计算方式决定的
- 掌握神经网络结构的精髓后，我们可以把它当作拼图一样看待，如果你对OpenAI的各种模型有所了解就会发现，他的模型都是将基本结构进行的简单组合，而这也正是大模型的内涵（简单拓扑结构但是庞大的数据量）

使用pytorch的nn.Sequential可以构建一个基本的网络序列，但是为了能够实现拼图一样的思路，我们使用类继承的方式完成：

# 全连接神经网络
class FNN(nn.Module):
    def __init__(self):
        # 实现基类构造
        super(FNN, self).__init__()
        # 一层全连接层，输入1，输出1
        # 输入层
        self.layer1 = nn.Linear(1, 1)

    def forward(self, x):
        # 前传
        x = self.layer1(x)
        return x

如此简单就实现了FNN类，只需要对他实例化即可使用这个模块，当然我们也可以叫他线性拟合器（名字而已，随便叫）

接下来实现训练过程，训练需要用到网络，输入量，理论输出量，更新器(optimizer)和损失函数(loss)，损失函数负责计算实际输出和理论输出之间的差距，更新器主要负责训练网络本体：

def train(net, x, y, optimizer, loss):
    # 训练1000次
    for i in range(1000):
        y_hat = net(x)
        # 计算损失
        l = loss(y_hat, y)
        optimizer.zero_grad()
        # 反传
        l.backward()
        optimizer.step()
        # 每100次输出一次损失
        if i % 100 == 0:
            print('epoch %d, loss %.4f' % (i, l.item()))
    return net

---

常用损失函数

• 香农熵

$$H(x)=-\sum_xp(x)·log\,p(x)$$

香农熵也是最基本的信息熵，它用于衡量数据的不确定性也相当于一种分散程度

• 交叉熵（CrossEntropyLoss）

$$H(p,q)=-\sum_xp(x)·log\,q(x)$$

对于两组信息p和q，交叉熵用于衡量这两组信息不确定性的差异，也相当于分散的差异，对于两组不同的分布，可以用交叉熵衡量分布的差异

• 相对熵（KL散度 KLDivLoss）

$$KL(p||q)=-\sum_xp(x)·log\,\frac{q(x)}{p(x)}$$

相对熵也叫KL散度，相对熵是在距离空间上衡量两者距离，KL散度则是衡量不相似性

其中有一个恒等式

$$H(p,q)=H(p)+H(p||q)$$

• Softmax函数（SoftMarginLoss）

$$Softmax(x)=\frac{e^{y_i}}{\sum_{n=1}^{N}e^{y_n}}$$

其中y对应了不同情况下的的输出值，得出的结果非负且和等于1

• SVM损失函数（凸优化损失函数）

$$L=\sum_{j≠y_i}\,MAX(0,s_j-s_{y_i}+1)$$

• MSE损失函数（均方损失函数）

$$L(\hat y, y)=\frac{1}{2}(\hat y-y)^2$$

优化方法

• 梯度下降法(SGD)

梯度是高等代数的内容，对于一个多元函数f(x,y,z)，他的梯度用$\nabla$表示，计算方法为：

$$\nabla f(x,y,z)=\frac{\partial f(x,y,z)}{\partial x}\vec i+\frac{\partial f(x,y,z)}{\partial y}\vec j+\frac{\partial f(x,y,z)}{\partial z}\vec t$$

梯度本身就是一种方向导数，所以当梯度最大时，坡度也就最大。梯度下降的表达式为：

$$\theta=\theta_0-\eta \nabla f(x,y,z)$$

其中$\eta$是步长，通过迭代$\theta$就可以实现优化。

• 动量法(Adam)

根据物理的动量守恒公式，得到函数的最低点。其中梯度的计算公式为：

$$gard=\frac{1}{m}\nabla \sum _{i=1}^{n}Lose(x,f(x))$$

速度更新是在下滑过程中有摩擦，所谓摩擦实际上是对速度的变化。μ为摩擦，gard就是梯度

$$v=μv+gard$$

权重更新，α是学习率，v为实时的速度。

$$\theta=\theta-\alpha v$$

同理衍生出Adagard，即改变不同位置不同方向上的学习率，δ为稳定用的数值，一般为$10^{-5}$，改变的规则为：

$$\omega=\omega-\frac{ε}{\sqrt{r}+\delta}\theta$$

其中的r为梯度的累加值，即：

$$r=r+(grad)^2$$

自适应也有RMSPorp。

---

最后给出main方法：

if __name__ == "__main__":
    # 生成数据
    x, y = generate_data()
    net = FNN()
    # 损失为均方误差
    loss = nn.MSELoss()
    # 优化器为随机梯度下降，lr为学习率
    optimizer = optim.SGD(net.parameters(), lr=0.1)
    net = train(net, x, y, optimizer, loss)
    # 顺便画个图
    plt.scatter(x, y)
    # 画出拟合的直线
    plt.plot(x, net(x).detach().numpy(), 'r-')
    # 展示！
    plt.show()

看看效果吧~

# 终端
epoch 0, loss 16.7385
epoch 100, loss 0.0757
epoch 200, loss 0.0741
epoch 300, loss 0.0740
epoch 400, loss 0.0740
epoch 500, loss 0.0740
epoch 600, loss 0.0740
epoch 700, loss 0.0740
epoch 800, loss 0.0740
epoch 900, loss 0.0740

反向传播方法我也复述一下：

正向传播

假设一个感知器有n个输入，激活函数假定为sigmoid（σ）那么我们有：

$$a_i=\sigma(\sum_i ω_ix_i+b)$$

所以最终输出值的偏导数基于链式法则就是：

$$\frac{\partial a_n}{\partial x_α}=\prod_{i}^{n} \frac{\partial a_i}{\partial x_i}$$

根据这个表达式，我们得到的就是反向传播

反向传播

如果我们知道最后的结果以及表达式，基于链式法则，我们可以求出各层的梯度，所以反向传播公式就是：

$$\prod_{i}^{n} \frac{\partial a_i}{\partial x_i} = \frac{\partial a_n}{\partial x_α}$$

虽然公式与正向传播相似，但是意义不同

卷积神经网络

这部分其实与计算机视觉有很大关系，神经网络实现的计算机视觉也叫深度视觉，其实卷积神经网络很早很早前就说过了，这里再叙述一遍：

• 卷积神经网络运用卷积算法计算矩阵之间的乘积，卷积计算对两个矩阵的大小没有严格规定，数学原理可以看：卷积神经网络与傅里叶变换的关系
• 一个卷积层里面可能有很多个用于计算和学习的卷积核，他们彼此之间有差异，比如处理一个通道可能有三个卷积核，这些卷积核计算的结果各自独立，并不会互相交换数据
• 卷积层与输入通道有很大关系，比如输入通道有3个（图片的RGB），不同通道同一个位置的卷积核计算结果进行加和，最后得到的输出通道数与每个通道处理的卷积核数量有关，比如RGB三层，每层都有10个卷积核，那么输出通道就是10
• 池化层会根据池化半径将输出尺寸进行除法取整，

用pytorch实现的话，我用mnist数据集实现，因为数据都是单通道的（灰度图），所以输入通道设置为1即可，那么我们的流程就确定了：

• 获取数据集
• 构建CNN模型
• 训练并测试

非常简单，对吧~，首先完成第一步：获取训练集和测试集，这里用了torch自带的下载方式。

train_loader = torch.utils.data.DataLoader(
    # 第一个参数是数据集的路径, 可以修改
    # download=True: 如果数据集不存在则下载
    datasets.MNIST('data', train=True, download=True,
                   # transform: 对数据集进行预处理，这里是将数据集转换为tensor并归一化
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    # batch_size: 每次读取的数据个数(512大概占显存1G)
    # shuffle: 是否打乱数据集
    batch_size=512, shuffle=True)

# 测试集
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    # 降低测试时间
    batch_size=256, shuffle=True)

接下来确定网络形状，mnist每个图片都是28×28的，用NCWH表示就是[b,1,28,28]，其中b就是样本数：

class CNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.model = nn.Sequential(
            # mnist是一张灰度图，所以输入通道数为1，长宽为28
            # 一次一张，一张一个通道，长宽为28[1, 1, 28, 28]
            # Conv2d四个参数，第一个参数是输入通道数，第二个参数是输出通道数，第三个参数是卷积核大小，第四个参数是步长
            nn.Conv2d(1, 32, 3, 1),
            # 输出通道数为32，长宽为26，计算方式为(28-3+1)
            nn.ReLU(),
            nn.MaxPool2d(2),
            # 池化层，长宽除以2并向下取证，输出通道数不变
            # output shape: (32, 13, 13)
            nn.Conv2d(32, 64, 3, 1),
            # output shape: (64, 11, 11)
            # 输出通道数为64，长宽为11，计算方式为(13-3+1)
            nn.ReLU(),
            nn.MaxPool2d(2),
            # output shape: (64, 5, 5)
            # 一样的计算方法
            nn.Flatten(),
            # 取出所有参数，64个输出，每个输出都是长宽为5的矩阵
            nn.Linear(64 * 5 * 5, 128),
            nn.ReLU(),
            nn.Linear(128, 10)
        )

    def forward(self, x):
        return self.model(x)

如此一来，我们就有了网络模型，他是一个：

• 第一层输入尺寸28×28一张，输出26×26共32张特征图
• 第一层池化，池化半径为2，长宽都除以2并向下取整
• 第二层输入32通道，尺寸为13×13，输出为64通道，尺寸为11×11
• 第二层池化，池化半径为2，长宽都除以2并向下取整，最终输出有64通道，每个通道都是5×5
• 打平层与池化输出参数量有关，因每个通道都是5×5，所以一共是64×5×5个参数，全连接后变成128个参数
• 最后输出层负责把128变成10个，也就是手写数字（0~9）

训练函数也要有，当然都放在cuda上运行，不然速度有点慢。

# 训练模型
'''
:param net: 神经网络
:param train_iter: 训练数据集
:param num_epochs: 训练次数
:param lr: 学习率
:param device: 设备(一般是cuda或者cpu，多个显卡会变成cuda1、cuda2等等)
'''
def train_ch6(net, train_iter, num_epochs, lr, device):
    net.to(device)
    print("training on", device)
    # Adam，当然还有其他的比如SGD等等
    optimizer = optim.Adam(net.parameters(), lr=lr)
    # 交叉熵损失函数(MSE也行,不过拟合速度没有交叉熵快)
    loss = nn.CrossEntropyLoss()
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n, start = 0.0, 0.0, 0, time.time()
        for X, y in train_iter:
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            train_l_sum += l.cpu().item()
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().cpu().item()
            n += y.shape[0]
        print('epoch %d, loss %.4f, train acc %.3f, time %.1f sec'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, time.time() - start))

同理，我们还需要一个测试函数计算输出准确率，测试函数和训练函数唯一区别就是不更新梯度：

def test(model, device, test_loader):
    # 切换模型为评估模式（不启用Dropout）
    model.eval()
    test_loss = 0
    correct = 0
    # 关闭梯度记录
    with torch.no_grad():
        # 遍历测试集
        for data, target in test_loader:
            # 全放在GPU
            data, target = data.to(device), target.to(device)
            # 计算输出
            output = model(data)
            test_loss += F.nll_loss(output, target, reduction='sum').item()  # 将一批的损失相加
            pred = output.max(1, keepdim=True)[1]  # 找到概率最大的下标
            correct += pred.eq(target.view_as(pred)).sum().item()  # 对预测正确的数据个数进行累加

    # 计算损失平均值
    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

最后就是调用这些方法：

if __name__ == "__main__":
    model = CNN()
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    train_ch6(model, train_loader, 5, 0.001, device)
    test(model, device, test_loader)

我们看一下输出：

training on cuda
epoch 1, loss 0.0007, train acc 0.908, time 12.3 sec
epoch 2, loss 0.0002, train acc 0.976, time 14.7 sec
epoch 3, loss 0.0001, train acc 0.984, time 8.4 sec
epoch 4, loss 0.0001, train acc 0.986, time 7.9 sec
epoch 5, loss 0.0001, train acc 0.990, time 11.0 sec

Test set: Average loss: -13.8237, Accuracy: 9885/10000 (99%)

可以看到，准确率高达99%，证明我们的网络成功运行了

循环神经网络

RNN实现也非常简单，只需要按照之前说过的定义顺序即可，这里给出RNN的数学原理传送门：https://blog.minloha.cn/posts/172730dca99de52022112710.html

这里我要实现一个时间序列预测（效果非常差）用于展示RNN的结构，一般很少使用到RNN而是使用更为严谨了LSTM或者GRU等等，但是也不能不说，所以就写一下：

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()
        self.net = nn.RNN(input_size, hidden_size, num_layers=1, batch_first=True)
        self.fc = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        out, _ = self.net(x)
        out = self.fc(out[:, -1, :])
        return out

RNN需要进行两次运算，一次对记忆内容重新处理，一次对输入进行计算，这两个我们可以叫H层和O层，其中H层是对上次输出进行记忆输入，O层是针对此次输入进行计算输出。

$$h_t=f(z_t)$$

其中我们的$z_t$等于如下形式：

$$z_t=Uh_{t-1}+Wx_t+b$$

而输出有：

$$o_t=Vh_t+c$$

反向传播算法BPTT就是根据时间进行反向学习，这当然很简单：

首先我们需要一个损失函数L，我们让损失函数关于前一时刻的输出进行建立关系：

$$\frac{\partial L}{\partial u_{ij}}=\sum_{k=1}^t\frac{\partial L}{\partial z_k}\frac{\partial z_k}{\partial u_{ij}}$$

解释一下这个微分，他表达损失函数关于第ij个循环节点的参数的偏微分，因为循环神经网络是有时间关系限制，所以我需要将所有时间的链式法则进行加和，最后就是基本的链式法则表达时刻t节点(i,j)的微分。为了包含进所有记忆体，我们将链式结构在时间上展开：

$$\frac{\partial L}{\partial z_k}=\frac{\partial h_k}{\partial z_k}\frac{\partial z_{k+1}}{\partial h_k}\frac{\partial L}{\partial z_{k+1}}$$

为了便于表示我们定义一个误差变量，它的计算依然是链式法则，写出对应项即可：

$$\delta_k = \frac{\partial L}{\partial z_k} = Ef'(z_k) U^T \delta_{k-1}$$

其中E是单位矩阵，负责把激活函数的导数值变成矩阵形式（导数值应为向量），这样我们可以有最终的计算公式：

$$\frac{\partial L}{\partial U}=\sum_{k=1}^t\delta_{t,k}h_{t,k-1}^T$$ $$\frac{\partial L}{\partial W}=\sum_{k=1}^t\delta_{t,k}x_{k}^T$$ $$\frac{\partial L}{\partial b}=\sum_{k=1}^t\delta_k$$

关于输出过程的迭代可以很容易的计算：

$$\frac{\partial L}{\partial V}=\frac{\partial L}{\partial o_t}h_t^T$$ $$\frac{\partial L}{\partial b}=\frac{\partial L}{\partial o_t}$$

这部分可以去查看我的往期博客：https://blog.minloha.cn/posts/172730dca99de52022112710.html

言归正传，我们再完成数据集处理部分，这里我在github随便找了一个csv文件进行序列预测，

file = "serial.csv"
TRAIN = 0.7  # 训练数据占比


def getData():
    # 读取文件,但是只读第二列(第一列都是日期,不如用1开始的数字代替)
    df = pd.read_csv(file, usecols=[1])
    # 剔除其中的非数字NAN
    data_csv = df.dropna()
    # 获取值
    dataset = data_csv.values
    # 转变类型为float32,默认为long
    dataset = dataset.astype('float32')
    # 取出其中的平均值
    scalar = np.max(dataset) - np.min(dataset)
    # 做出键值映射,顺便做一下归一化
    dataset = list(map(lambda x: x / scalar, dataset))
    return dataset


'''
:param dataset 数据集
:param step 预测步长(步长在一个合理的域效果好,不能过大或过小)
'''

def create_dataset(dataset, step=2):
    dataX, dataY = [], []
    for i in range(len(dataset) - step):
        a = dataset[i:(i + step)]
        # 拆开键值映射,取出其中的值
        dataX.append(a)
        dataY.append(dataset[i + step])
    # 返回数据(这时不分训练集和测试集)
    return torch.tensor(np.array(dataX)), torch.tensor(np.array(dataY))

然后我们确定一下训练方法，当然和前文叙述过的大同小异，无非就是给网络和训练数据，根据学习率和优化器进行反向传播：

def train(net, x, y, optimizer, loss):
    # 迭代80次去学数据集
    for i in range(80):
        y_hat = net(x)
        # 计算损失
        l = loss(y_hat, y)
        optimizer.zero_grad()
        # 反传
        l.backward()
        optimizer.step()
        # 每10次输出一次损失
        if i % 10 == 0:
            print('epoch %d, loss %.4f' % (i, l.item()))

而测试方法自然就用测试集进行预测：

def test(net, x, y, loss):
    y_hat = net(x)
    l = loss(y_hat, y)
    # 绘制实际值y和预测值y_hat的图像
    plt.plot(y.numpy(), label='real')
    plt.plot(y_hat.detach().numpy(), label='predict')
    plt.legend()
    plt.show()
    print('test loss %.4f' % (l.item()))

然后我们在main方法里把数据集分割一下，按照TRAIN定义的0.7分割训练集和测试集：

def RNNtry(train_X, train_Y, test_X, test_Y):
    # 网络定义,数据重播用俩,希望能从历史中吸取更多教训
    net = RNN(1, 2, 1)
    # 优化器
    optims = optim.Adam(net.parameters(), lr=0.1)
    # 损失函数
    loss = nn.MSELoss()
    # 训练
    train(net, train_X, train_Y, optims, loss)
    test(net, test_X, test_Y)
    

if __name__ == "__main__":
	 # 获取数据集
    dataset = getData()
    # 创建数据集
    data_X, data_Y = create_dataset(dataset)
    train_size = int(len(data_X) * TRAIN) # 训练集大小,TRAIN就是训练集占总数的比例
    test_size = len(data_X) - train_size # 剩下的就测试用吧
    # 简单分割一下
    train_X = data_X[:train_size]
    train_Y = data_Y[:train_size]
    test_X = data_X[train_size:]
    test_Y = data_Y[train_size:]
    # 单独定义函数(方便之后优化)
    RNNtry(train_X, train_Y, test_X, test_Y)

然后我们看看运行效果，查看一下我们的学习效果：

epoch 0, loss 0.0753
epoch 10, loss 0.0158
epoch 20, loss 0.0050
epoch 30, loss 0.0029
epoch 40, loss 0.0029
epoch 50, loss 0.0022
epoch 60, loss 0.0021
epoch 70, loss 0.0020
test loss 0.0102

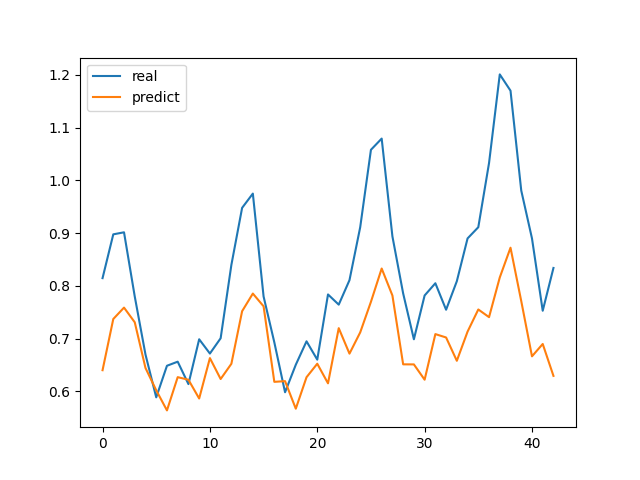
绘制的图像如图：

从输出数据上我们可以看到损失值在直线降低，而从图像上我们看到测试集的误差不太美观甚至差距有点大了，原因是RNN本身结构的缺陷：

• RNN没办法指定遗忘，所以就产生了一个长程依赖问题，学术的说就是长期学习让回忆内容的权重被大量未来数据影响变低了，通俗的说就是记得太多学杂了

而这种长程依赖问题就可以用LSTM（长短期记忆网络）或者GRU（门控循环单元）去解决，这个放到下次博客吧~

总结

本期博客内容非常干，读者可以快速学会各种基础神经网络的结构，同时使用了pytorch(不用tensorflow，没有torch写起来容易)实现了全部功能，相信坚持下去一定会有明显进步吧~

本期博客代码开源，开源地址为：https://github.com/iMinloha/TorchPro.git