机器人学基础——控制方法

介绍

本期内容主要是控制方法，但不要提到控制方法就想到PID，虽然本人也非常喜欢用PID。PID只是一种性价比较高的控制器，容易写并且消耗较低，应用范围也很广。但是复杂系统一般不会用PID控制。原因也很简单，PID就是比例+积分+微分，如果按传递函数讲，他就是一个二阶传递函数，也就意味着一个PID不可能控制超过二阶的系统。现实情况往往非常复杂，所以我们不得不学习很多的新方法。所以本期博客就是在基本的控制理论基础上进行延拓。当然有些较为先进的控制算法可以去查阅相关文献，有些算法固然经典，但是无法适应时代的进步。

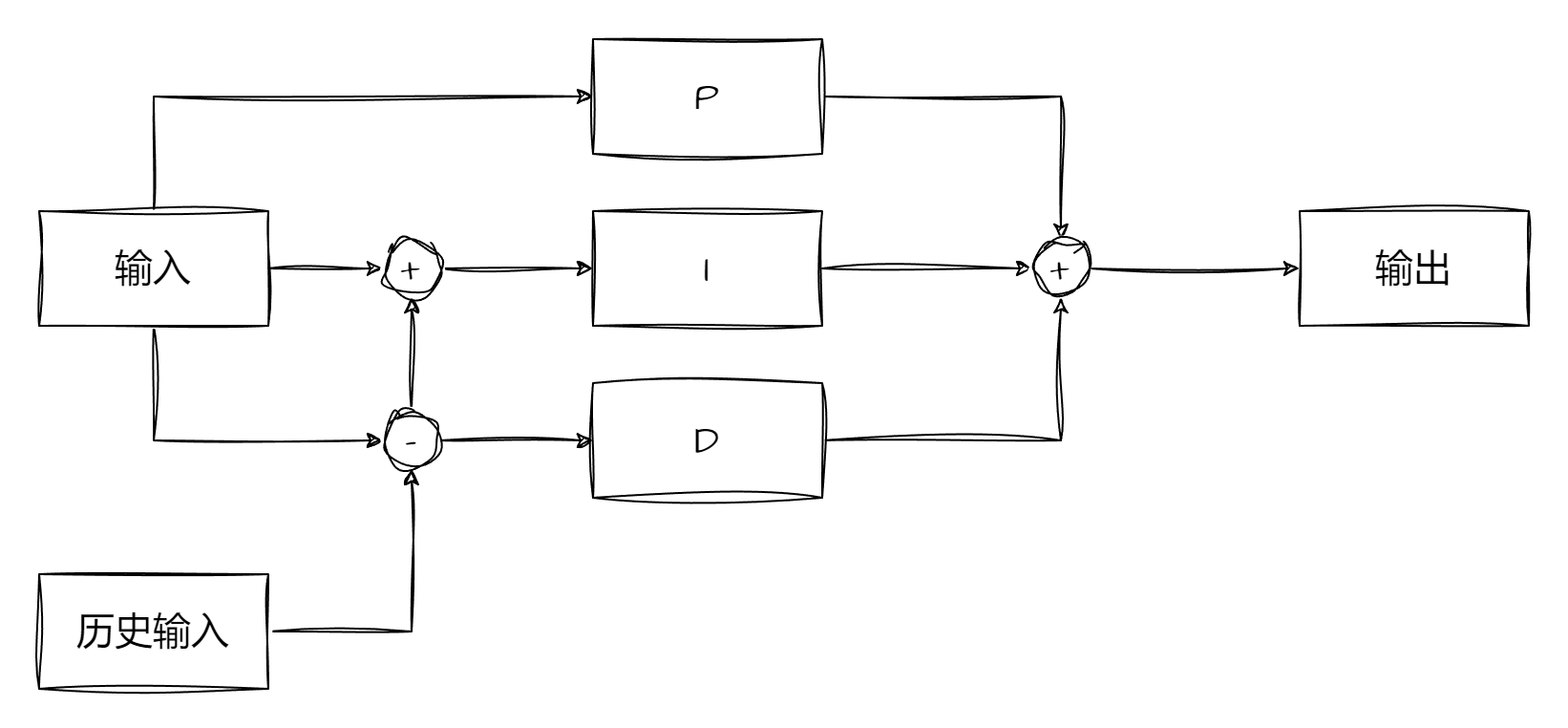
如图为基本的PID流程，这个过程几乎已经烂熟于心了，并且有不错的教材（自动控制原理）提及，所以本人就不过多赘述了。那么针对PID我们可以延伸出很多控制方法，诸如自适应PID、模糊PID、优化PID等。除了PID还有LQR这种基于惩罚函数的模型优化控制器，还有MPC这种纯粹的模型控制器等，所以我们无法单纯利用PID作为控制算法的中心，我们就需要抛开问题看本质，所以我们的控制器分类就按照控制方法进行了。

注意，划分的每一个章节都是一个单独的学科，章节名为学科名，内涵很多知识体系，因篇幅有限无法给出更多细节，所以如果不懂可以尝试搜索学习。

动力学建模

提到建模很多人都会有不同的联想对象，我这里说的是动力学建模，对于一个系统，他肯定可以用一定量的物理方程表示出来，无论是旋转的、摆动的、震荡的，这些都可以用数学表述。但是这些数学表述千奇百怪，我们必须要进行一定的约束，所以我们就需要进行专业的分析，首先我们需要给出状态方程的标准格式：

$\dot x=Ax+Bu$ $y=Cx$

如上，这是最为基本的传递过程，其中x也叫状态向量，A叫做状态转移矩阵，B叫做输入控制矩阵，u为输入量，C为输出矩阵，y为输出量（并不参与控制）。对于一组数学表达式，我们总能转化为这种形式，我们可以用到线性代数的知识进行快速变化。当然也可以列些拉格朗日方程提取变量（这是个人感觉最快的，但是算量有点大）。我们以倒立摆举例：

倒立摆首先单摆可以写出力矩J，力矩可以用重物的质量m与摆长l的平方乘积表达：

$J=ml^2$

定义L为拉格朗日量，其大小为系统的总动能减总势能，其中动能的大小可以通过力矩计算，根据基本的物理公式计算得到：

$L=T-V=\frac{1}{2}J\dot \theta^2-(-mglcos(\theta))$

公式中的$\theta$为单摆的摆角，$\dot \theta$为摆角的一阶微分也就是角速度，再列写拉格朗日方程：

$\frac{\partial}{\partial t}\frac{\partial L}{\partial \dot \theta}-\frac{\partial L}{\partial \theta}=0$

分别求出$\frac{\partial}{\partial t}\frac{\partial L}{\partial \dot \theta}$和$\frac{\partial L}{\partial \theta}$带入所有变量带入拉格朗日方程化简得到：

$\ddot \theta = \frac{g}{l}sin(\theta)$

其中的g为重力加速度，是一个常量，而$\ddot \theta$为角度的二阶微分即角加速度。定义其状态变量可以得到：

$\dot x_1=x_2$ $\dot x_2=\ddot \theta=-\frac{g}{l}sin(x_1)$

将状态变量写作向量的形式就可以得到系统的状态向量表示为：

$x=\left[\begin{matrix} x_1\\ x_2 \end{matrix} \right]$

通过状态分量$x_2$可以发现这是一个非线性系统，为了书写其标准的状态空间方程，这里需要使其反馈线性化[13]，先进行输出方程的列写即：

$y=Cx=\left[\begin{matrix} 1 & 0 \end{matrix} \right]x$

引入控制变量u，假设存在一个状态空间模型，包含状态更新矩阵A和控制输入矩阵B，则满足：

$\dot x = Ax + Bu = \left[\begin{matrix} \dot \theta\\ \frac{g}{l}sin \theta \end{matrix} \right]+ \left[\begin{matrix} 0\\ \frac{1}{ml^2} \end{matrix} \right]u$

其中$\dot x$为状态向量的一阶微分，根据反馈线性化操作，可以通过同胚法或者李代数法[16]求出需要的反馈量。这里采用李代数法，求出C对x分量的导数$\frac{\partial C}{\partial x}$，得到：

$u=\frac{1}{\frac{\partial C}{\partial x} B}(\frac{\partial C}{\partial x} Ax + v)$

其中的v为外界输入的激励信号，将所有变量代入得到：

$u=\frac{1}{ml^2}(\frac{g}{l}sin \theta+v)$

通过这种方式，已经使得非线性项$\sin(\theta)$被反馈线性化处理掉，从而使得系统的动力学可以表示为一个线性系统，且控制输入v可以通过设计来控制系统的行为。对这个非线性系统可以把v设定为：

$v=-k(\theta+\dot \theta)$

这里的$k$为反馈增益系数，为常数。引入后可以得到状态方程为：

$\dot x=Ax+Bu= \left[\begin{matrix} 0 & 1\\ 0 & k \end{matrix} \right] x+ \left[\begin{matrix} 0\\ \frac{k}{ml^2} \end{matrix} \right] u$

而u又可以带入v的值，得到：

$u=\frac{1}{ml^2}(\frac{g}{l}sin \theta-k(\theta+\dot \theta))$

优化控制

提及优化，就很难不想到几种优化算法，大概可以分成有梯度和有约束函数两类，其中有梯度包括高斯牛顿法、狗腿法、动量法等等，约束函数又有惩罚函数，这些都是较为常用的优化方法，那么如何使用这些方法应用与控制领域就变成了如何转化这些方法。

动态规划

首先介绍DP（动态规划）方法，DP在算法题经常出现，其本质是一种牺牲空间换时间的方法，其算法可以间接的降低算法的时间复杂度，但是在控制领域，我们只需要考虑DP对数据的保存，顺便制定一种对结果的评估，我们写出系统的状态转移方程，姑且引入时间项：

$\dot x(t)=Ax(t)+Bu(t)=f(x(t),u(t),t)$

同时还需要对系统进行结果评估，我们引入一个评判函数用于评判系统：

$J=\int_{t_0}^{t_n}L(x(t),u(t),t)+\phi(x(t_{n}))$

式子中出现了$\phi(x(t_{n}))$，它可以理解为一个惩罚项，而L函数可以看作在$t_0到t_n$这段时间内的误差累计。由实际可知我们无法连续分析，对此我们引入离散状态下的贝尔曼方程（就是强化学习基础的贝尔曼方程）：

$V(x_k,t_k)=\min_{u_k}[L(x_k,u_k)\Delta t+V(x_{k+1},t_{k+1})]$

注意，这是一种在时间上的递推，并且是满足增量关系即：

$x_{k+1}=x_k+f(x_k,u_k)\Delta t$

其中的$\Delta t$ 是时间的微分，如果足够小就会使得这个方程变成微分方程，也就是著名的HJB方程：

$-\frac{\partial V}{\partial t}(x,t)=\min_{u}[L(x,u,t)+\nabla_x V(x,t)f(x,u,t)]$

而最优控制输出就是u，其值应使得梯度最小即目标值$u^*$应：

$u^*=arg \min_{u}[L(x,u,t)+\nabla_x V(x,t)f(x,u,t)]$

有了优化方法就可以将他融入到控制器，这里选择LQR方法：

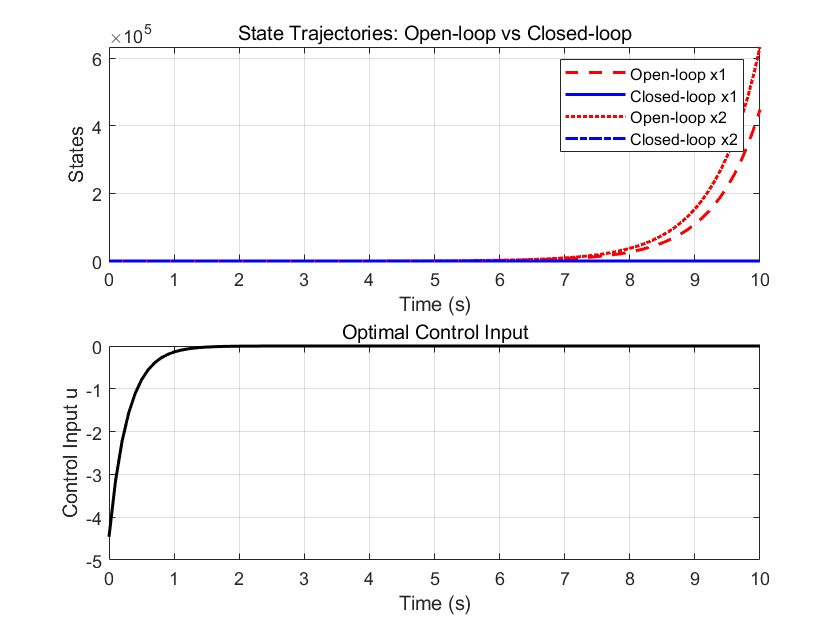
可以看到简单的倒立摆仿真效果非常好。

LQR方法

刚才提及到了LQR方法，这里我也说一下LQR方法，首先假设一个状态方程：

$\dot x=Ax+Bu$

其中A叫做状态转移矩阵，B叫做输入控制矩阵，通过状态转移得到下一瞬间的状态向量$\dot x$，而控制LQR的最小化代价函数J为：

$J=\int_0^\infty(x^TQx+u^TRu)dt$

其中Q与R均为对角矩阵，Q用于惩罚系统误差而R用于控制系统输入，为了最小化代价函数让J值最小，为此引入辅助矩阵P，可以使：

$x^TPx=-(x^TQx+u^TRu)$

假设系统是稳定的，这样最小化J可以写作：

$J=\int_0^\infty\frac{d}{dt}x^TPxdt=x^T(0)Px(0)$

结合可以计算得到：

$A^TP+PA+Q+(R^{-1}B^TP)^TR(R^{-1}B^TP)\\ -(R^{-1}B^TP)^TB^TPP-PB(R^{-1}B^TP)=0$ $A^TP+PA+Q-PBR^{-1}B^TP=0$

这个方程也被叫做Algebraic Riccati Equation(ARE)[9]，这些内容可以通过仿真模型的建立进行计算，最终就会得到确切的辅助矩阵P，然后就可以利用下面的公式计算反馈增益矩阵K了。

$K=R^{-1}B^TP$

通过设定反馈矩阵就可以对系统进行控制了（基本的反馈控制思想，可以阅读现代控制理论一书），当然也可以尝试诸如反馈线性化、极点配置等老牌控制法。

Pontryagin最小值

庞特里亚金最大化原理

这也是一种最优化控制的重要方法，通过必要的变形可以变为Pontryagin最小值，与DP方法不同的是，它使用了变分法和哈密顿力学。

对此我们需要先下一个定义即，假设有一个最优控制u，那一定要满足：

状态方程与协态方程（共态方程）同时成立。
哈密顿函数在最优控制下取得全局最小值。

这里出现了优化控制理论的知识，补充一下：
哈密顿函数是连接状态方程和目标函数的关键桥梁。其定义为：
$H(x,y,\lambda,t)=L(x,u,t)+\lambda(t)f(x,u,t)$
式子中的L是目标函数的瞬时成本（简单理解为目标函数），$\lambda$可以看作拉格朗日量，在方程内被称为协态变量。而f函数是状态的输入，一般写作u项
协态方程就是对哈密顿方程求x方向的偏导数得到$\lambda$与哈密顿方程的关系即：
$\dot \lambda(t)=-\frac{\partial H}{\partial x}$

归纳整理为数学语言就是：

1、状态方程

$x^*(t)=\frac{\partial H}{\partial \lambda}=f(x,u,t)$

2、协态方程

$\lambda ^ *(t)=-\frac{\partial H}{\partial x}$

3、最小值条件

$H(x^*(t),u^*(t),\lambda ^*(t),t)=\min H(x^*(t),u,\lambda ^*(t),t)$

接下来举个例子：

将小车从初始位置 $x(0) = x_0$ 移动到原点 $ x(t_f) = 0$，时间$t_f$最小化。

首先我们知道系统的位置x直接受到u的控制，所以可以写作：

$\dot x(t)=u(t)$

利用评判函数，且优化到$t_f$可知，$J=t_f$：

$J=\int_{0}^{t_f}L(x(t),u(t),t)+\phi(x(t_{n}))=t_f$

简单换个元就得到：

$\int_{0}^{t_f}L(x(t),u(t),t)=t_f$

所以L=1，我们得到哈密顿方程：

$H=1+\lambda u$

协态方程1可以写成：

$\dot \lambda(t)=-\frac{\partial H}{\partial x}=0$ $\lambda (t)=\lambda_0$

所以$\lambda$全程保持不变，并且为了满足哈密顿函数的最小值，选择合适的u，从哈密顿方程分类讨论：

$\lambda_0>0$，则$u^*=-1$
$\lambda_0<0$，则$u^*=1$

将解带回到状态方程，分别得到两个解：

$x(t)=x_0-t$

假设到达原点解出：到达原点时间为$t_f=x_0$满足事实。带入第二个情况得到：

$x(t)=x_0+t$

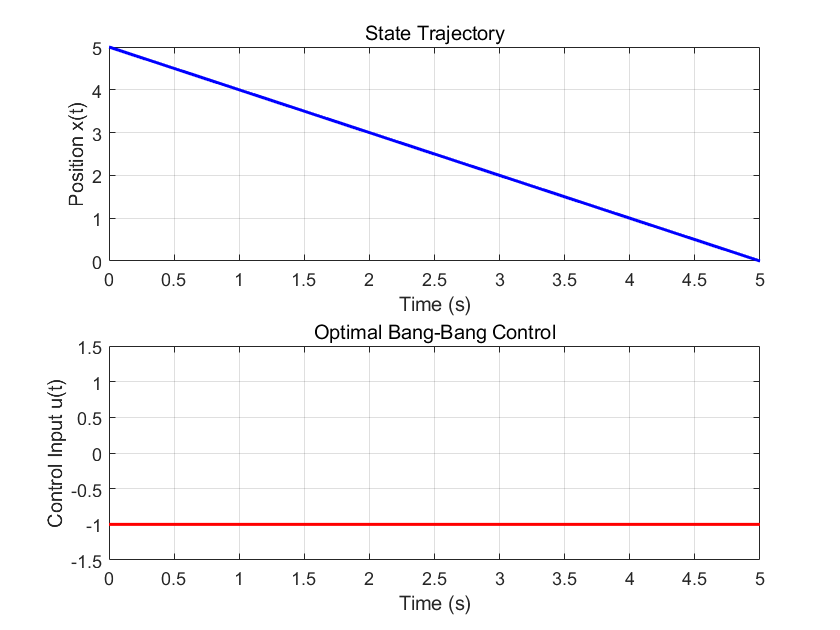
到达原点时间为$t_f=-x_0$，与目标矛盾，舍去。因这个例子中u仅有两组选择，我们引入Bang-Bang Control，也就是二值控制算法：

% 最短时间控制问题（Bang-Bang控制）
clear; clc;

% 系统参数
x0 = 5;   % 初始位置
u_max = 1;% 最大控制输入

% 解析解：最短时间 t_f = x0 / u_max
t_f = x0 / u_max;
t = linspace(0, t_f, 100);
x = x0 - u_max * t;
u = -u_max * ones(size(t));

% 绘图
figure;
subplot(2,1,1);
plot(t, x, 'b-', 'LineWidth', 1.5);
xlabel('Time (s)'); ylabel('Position x(t)');
title('State Trajectory');
grid on;

subplot(2,1,2);
plot(t, u, 'r-', 'LineWidth', 1.5);
ylim([-1.5, 1.5]);
xlabel('Time (s)'); ylabel('Control Input u(t)');
title('Optimal Bang-Bang Control');
grid on;

绘制曲线得到位置和输入曲线，看起来很简单，就是保持一个值的递减，但是仅此而已罢了：

模型控制

模型控制或者说模型预测控制(MPC)，它是一种基于滚动时域优化的控制策略，包含以下必要成分：

预测未来输出：利用系统模型预测未来一段时间内的状态或输出。
优化控制输入：在当前时刻求解一个有限时域的优化问题，得到最优控制序列。
实施首步控制：仅应用当前时刻的最优控制输入，下一时刻重新优化。
反馈校正：结合实际测量值修正预测模型，提升鲁棒性。

利用第一部分建模的知识我们很容易就能得到系统模型，当然这是一个连续的模型，我们可以前后差分得到离散模型即：

$x[k+1]=A'x[k]+B'u[k]$ $y[k]=Cx[k]$

而其前后关系为：

$A'=e^{AT_s}$ $B'=\int_0^{T_s}e^{A\tau}Bd\tau$

其中$T_s$为采样周期。单纯的MPC非常的单纯，所以我们必须给出更为深奥的控制器。

动态矩阵控制

DMC即动态矩阵控制，核心就是动态矩阵，其构建本质为系统的阶跃响应系数。按照步骤可以如下划分

1.建立动态矩阵

首先对系统进行建模，然后传递阶跃信号，记录阶跃响应序列$a=\{a_1,a_2,a_3…a_n\}$(传递阶跃信号一段离散时间的数据)，序列长度为N。

然后就可以构建动态矩阵A：

$A=\left[\begin{matrix} a_1 & 0 & \cdots & 0\\ a_2 & a_1 & \cdots & 0 \\ \vdots & \vdots & \ddots &\vdots \\ a_n & a_{n-1} & \cdots & a_1 \end{matrix} \right]$

而这个矩阵是N行N列，但是系统可能在响应序列第M位就趋于稳定了，并且很容易知道M<N，所以我们需要对A进行截断，截断位置就是M处。同时还要迎合输入长度，即矩阵变为：

$A=\left[\begin{matrix} a_1 & 0 & \cdots & 0\\ a_2 & a_1 & \cdots & 0 \\ \vdots & \vdots & \ddots &\vdots \\ a_{p} & a_{p-1} & \cdots & a_{p-m+1} \end{matrix} \right]$

其中的p为输入量维度，用于预测时域长度，决定需预测的未来输出步数。M则控制时域长度，决定优化变量的维度。

2.预测模型

模型的P步预测又可以表述为下式：

$\boldsymbol{Y}(k+1|k) = \boldsymbol{Y}_0(k+1|k) + A \Delta \boldsymbol{U}(k)$

$\boldsymbol{Y}(k+1|k)$：未来$P$步的预测输出向量。
$\boldsymbol{Y}_0(k+1|k$：基于过去控制输入的初始预测（无新控制增量时的自然响应）。
$\Delta \boldsymbol{U}(k)$：未来 $M$ 步的控制增量向量 $[\Delta u(k), \Delta u(k+1), …, \Delta u(k+M-1)]^T$。
动态矩阵$A$的维度为$P \times M$。

3.优化目标函数

然后我们需要优化目标函数，DMC通过最小化跟踪误差和控制增量的加权和来求解最优控制：

$J = \|\boldsymbol{Y}_{ref} - \boldsymbol{Y}(k+1|k)\|^2_Q + \|\Delta \boldsymbol{U}(k)\|^2_R$

$\boldsymbol{Y}_{ref}$：参考轨迹(未来P步的期望输出)。
Q与R：误差与控制增量的权重矩阵（通常为对角阵）

然后将预测模型代入目标函数，进行复杂的计算得到：

$J = \|\boldsymbol{Y}_{ref} - (\boldsymbol{Y}_0 + A \Delta \boldsymbol{U})\|^2_Q + \|\Delta \boldsymbol{U}\|^2_R$

求解得到无约束的解析解，通过求导并令导数为零，得到最优控制增量：

$\Delta \boldsymbol{U}^* = (A^T Q A + R)^{-1} A^T Q (\boldsymbol{Y}_{ref} - \boldsymbol{Y}_0)$

关键矩阵：$A^T Q A + R$ 必须可逆（通常通过设计权重保证）。
实时性：若系统参数固定，可预先计算逆矩阵以减少在线计算量。

到此已经完成了基本的步骤，接下来进行递归操作：

4.首步控制

仅采用当前时刻的最优控制增量 $\Delta u(k)$，更新控制输入：

$u(k) = u(k-1) + \Delta u(k)$

后续时刻重新执行预测和优化（滚动时域）。

5.反馈校正

由于模型误差和扰动，预测输出$\boldsymbol{Y}_0$可能与实际输出存在偏差。

校正方法*：

在时刻k，测量实际输出y(k)。
计算预测误差：$e(k) = y(k) - \hat{y}(k|k-1)$。
修正未来预测输出：
1. $\boldsymbol{Y}_0^{\text{new}} = \boldsymbol{Y}_0^{\text{old}} + \boldsymbol{H} \cdot e(k)$
2. 其中$ \boldsymbol{H}$为误差校正向量（通常取单位向量或滤波后的权重）。

最实用的部分便是如何设计参数，这里需要设定的参数很多，我写几个列表

对于时域P而言：

覆盖系统主要动态响应（P > M， M为截断处的长度)
如果过大就会对干扰敏感
过小就会导致控制激进

对截断长度M而言：

如果M很小则非常保守，变化很慢
如果M很大则响应速度加快，但是会增加计算量（A的维度）

Q与R：

增加Q就是让系统跟踪性能优先，可能引发控制量波动。
增加R就是控制增量抑制，系统响应变慢。

如果系统有约束则会变成二次规划问题，这里不多赘述，下面给出matlab仿真代码；

% DMC参数定义
clear; clc;

% 系统参数（一阶离散系统）
Ts = 1;         % 采样时间
sys = tf(1, [10 1]);  % 连续系统 G(s) = 1/(10s+1)
sys_d = c2d(sys, Ts); % 离散化
[A_d, B_d, C_d, D_d] = ssdata(sys_d);

% 阶跃响应生成（用于构建动态矩阵）
N = 30;         % 模型截断长度（阶跃响应趋于稳定的时间步数）
step_response = step(sys_d, 0:Ts:(N-1)*Ts); % 获取阶跃响应序列

% DMC参数
P = 20;         % 预测时域（Prediction Horizon）
M = 5;          % 控制时域（Control Horizon）
Q = eye(P);     % 输出权重矩阵（跟踪误差）
R = 0.1 * eye(M); % 控制增量权重矩阵（抑制输入变化）

% 构建动态矩阵A（关键步骤）
A = zeros(P, M);
for i = 1:P
    for j = 1:M
        if (i-j+1) > 0
            A(i,j) = step_response(i-j+1);
        else
            A(i,j) = 0; % 未到达影响时间
        end
    end
end

% 初始化变量
k_max = 100;    % 总仿真步数
y = 0;          % 初始输出
u = 0;          % 初始控制输入
y_history = zeros(1, k_max); 
u_history = zeros(1, k_max);
ref = 1;        % 参考轨迹（设定值）

% 初始化预测输出向量
Y0 = zeros(P, 1); % 初始预测输出（无未来控制增量）

% 滚动优化循环
for k = 1:k_max
    % --- 1. 测量当前输出（含噪声模拟实际系统） ---
    y_measure = y + 0.01*randn(); % 添加测量噪声
    
    % --- 2. 反馈校正：修正预测初始值 ---
    error = y_measure - Y0(1);    % 当前预测误差
    Y0 = Y0 + error * ones(P,1);  % 简单全时域误差补偿
    
    % --- 3. 计算参考轨迹（可选柔化）---
    Y_ref = ref * ones(P, 1);     % 阶跃参考
    
    % --- 4. 计算最优控制增量 ---
    DeltaU = (A' * Q * A + R) \ (A' * Q * (Y_ref - Y0)); % 无约束优化
    delta_u = DeltaU(1);          % 仅取当前时刻的控制增量
    
    % --- 5. 施加控制输入（带约束）---
    u_new = u + delta_u;
    % 输入约束（示例：幅值限制）
    u_new = max(min(u_new, 2), 0); % 限定输入范围 [0, 2]
    delta_u_actual = u_new - u;   % 实际可执行的控制增量
    
    % --- 6. 更新系统状态（真实系统仿真）---
    y = A_d * y + B_d * u_new;    % 一阶系统状态更新
    
    % --- 7. 更新预测初始值Y0 ---
    % 使用动态模型预测未来自然响应（无新控制增量）
    Y0 = [Y0(2:end); Y0(end)];    % 平移预测窗口
    Y0 = Y0 + A(:,1:M) * [delta_u_actual; zeros(M-1,1)]; % 叠加控制影响
    
    % --- 8. 记录数据 ---
    y_history(k) = y;
    u_history(k) = u_new;
    u = u_new; % 更新控制输入
end

% --- 可视化结果 ---
figure;
subplot(2,1,1);
plot(1:k_max, y_history, 'b-', 'LineWidth', 1.5); hold on;
plot(1:k_max, ref*ones(1,k_max), 'r--', 'LineWidth', 1.5);
xlabel('Time Step'); ylabel('Output');
title('DMC Control: Output vs Reference');
legend('Actual Output', 'Reference');
grid on;

subplot(2,1,2);
stairs(1:k_max, u_history, 'm-', 'LineWidth', 1.5);
xlabel('Time Step'); ylabel('Control Input');
title('Control Input');
grid on;

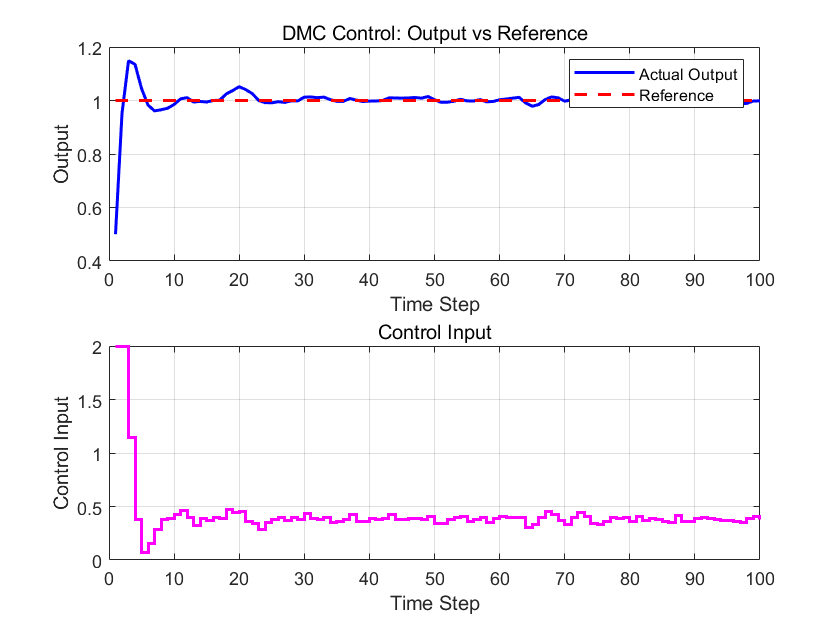
曲线可以看到我们的收敛时间非常非常快，虽然有点过冲，可以尝试调大P。但是总体效果非常好。

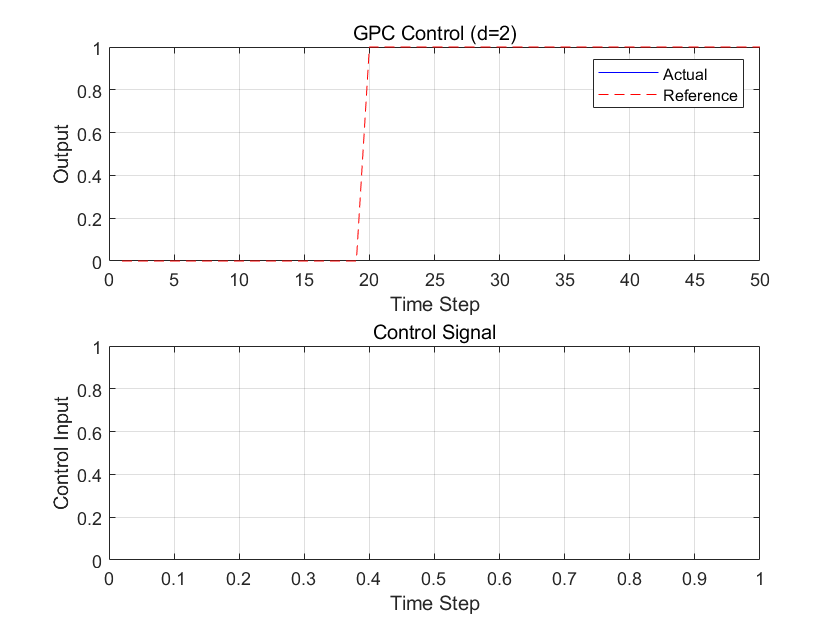
GPC

GPC也叫做广义预测控制，其本质基于数学模型CARIMA模型，通过多步优化进行控制，对比如下：

特性	GPC	DMC
模型类型	参数模型（CARIMA）	非参数模型（阶跃响应/脉冲响应）
噪声处理	显式建模随机扰动	依赖反馈校正
适用场景	随机扰动显著、模型复杂度高	确定性系统、低维动态
在线计算	需递归求解Diophantine方程	动态矩阵预计算
参数自适应性	支持在线参数估计（自校正GPC）	固定模型参数

首先介绍一下CARIMA模型，其表达式的原始形式如下：

$A(z^{-1}) y(k) = B(z^{-1}) z^{-d} u(k-d) + \frac{C(z^{-1})}{\Delta} e(k)$

当然常见的会设$C=1$进而得到简单表达式，经过简单的运算得到下面的格式：

$A(z^{-1}) \Delta y(k) = B(z^{-1}) \Delta u(k-d) + e(k)$

$d$ 为系统延迟步数, $e(k)$为零均值白噪声。
$\Delta = 1 - z^{-1}$：差分算子，用于消除稳态误差（积分作用）。
$A(z^{-1}) = 1 + a_1 z^{-1} + \cdots + a_{n_a} z^{-n_a}$：输出的自回归多项式。
$B(z^{-1}) = b_0 + b_1 z^{-1} + \cdots + b_{n_b} z^{-n_b}$：输入的滑动平均多项式。
$d$：系统延迟步数（输入到输出的延迟）。
$e(k)$：白噪声。

观察发现，这是一个针对离散系统的传递函数，其中的Z为特殊的拉普拉斯变换数值，即：$z=e^{j\omega}$，举个例子：

$y(k) = 0.9 y(k-1) + 0.1 u(k-2) + e(k)$

化成要求的格式得到：

$y(k) - 0.9y(k-1) = 0.1 u(k-2) + e(k)$

为此左右两边同时乘以差分算子得到：

$\Delta[ y(k) - 0.9y(k-1)] =\Delta[ 0.1 u(k-2) + e(k) ]$

展开得到：

$\Delta y(k) - 0.9z^{-1}\Delta y(k) = 0.1 \Delta u(k-2) + \Delta e(k)$

根据标准形式可以看出我们仅需处理$\Delta e(k)$，即：

$\Delta e(k) = e(k)-e(k-1)=e(k)-z^{-1}e(k)$

所以得到：

$(1- 0.9z^{-1})\Delta y(k) = 0.1 \Delta u(k-2) + (1-z^{-1}) e(k)$

列些其中的关键项即：

$A(z^{-1})=1- 0.9z^{-1}$ $B(z^{-1}) = 0.1$ $C(z^{-1})=1$ $d=2$

这里我重点强调一下，d本身并不为零，意味着系统天生存在2步滞后，这里很关键，在下文会用到

注意：差分算子是一种类似的积分算符，我尝试对整个方程进行了Z逆变换发现并不能得出求和或者积分项，原因也很简单，$\Delta$仅包含两个时刻的数据和，是一种等效的积分器，用表达式描述就是：

$u(k)=u(k-1)+\Delta u(k)\quad \Rightarrow \quad u(k) = \sum_{i=0}^k \Delta u(i)$

建立了CARIMA模型后我们需要进行长时间的预测，这里需要介绍一下Diophantine方程分解，这是一种对模型的处理，能够将模型分解为自由响应（过去输入输出的影响）和受控响应（未来输入的影响），我们需要通过递归求解Diophantine方程得到多项式 $G_j, F_j$，方程的标准形式如下：

$1 = E_j(z^{-1}) A(z^{-1}) \Delta + z^{-j} F_j(z^{-1})$

其中的j为步数，要求E和F的值，其值为多项式，如下：

$E_j(z^{-1}) = e_0 + e_1 z^{-1} + \cdots + e_{j-1} z^{-(j-1)}$ $F_j(z^{-1}) = f_0 + f_1 z^{-1} + \cdots + f_{n_a} z^{-n_a}$

而代求的$G_j$项又存在等式：

$G_j(z^{-1}) = E_j(z^{-1}) B(z^{-1})$

这样做的目的就是将未来输出$y(k+j)$ 分解为两部分：

自由响应（Free Response）：由历史输入和当前状态决定的自然响应$ F_j y(k)$。
受控响应（Forced Response）：由未来控制输入决定的响应$G_j \Delta u$。

我们继续按照之前的例子，假设j=1开始：

$1 = E_1 (1 - 0.9 z^{-1})(1 - z^{-1}) + z^{-1} F_1$

而j=1时，$E_1=e_0, F_1=f_0+f_1z^{-1}$，我们带入得到：

$1 = e_0 (1 - 1.9z^{-1} + 0.9z^{-2}) + f_0 z^{-1} + f_1 z^{-2}$

我们分别匹配$z^{0}、z^{-1}、z^{-2}$指数分别得到：

$1 = e_0 \cdot 1 \quad \Rightarrow \quad e_0 = 1$ $0 = e_0 (-1.9) + f_0 \quad \Rightarrow \quad -1.9 \cdot 1 + f_0 = 0 \quad \Rightarrow \quad f_0 = 1.9$ $0 = e_0 (0.9) + f_1 \quad \Rightarrow \quad 0.9 \cdot 1 + f_1 = 0 \quad \Rightarrow \quad f_1 = -0.9$

最终得到：

$E_1(z^{-1}) = 1, \quad F_1(z^{-1}) = 1.9 - 0.9 z^{-1}$

继续推理，当j=2时我们得到表达式：

$1 = E_2(z^{-1}) \cdot (1 - 0.9z^{-1})(1 - z^{-1}) + z^{-2} F_2(z^{-1})$ $1 = E_2(z^{-1}) (1 - 1.9z^{-1} + 0.9z^{-2}) + z^{-2} F_2(z^{-1})$

展开表达式得到：

$1 = (e_0 + e_1 z^{-1}) (1 - 1.9z^{-1} + 0.9z^{-2}) + z^{-2} (f_0 + f_1 z^{-1})$ $1 = e_0 (1 - 1.9z^{-1} + 0.9z^{-2}) + e_1 (z^{-1} - 1.9z^{-2} + 0.9z^{-3}) + f_0 z^{-2} + f_1 z^{-3}$

写作直观的表达式即：

$\begin{aligned} 1 &= e_0 \\ &+ (-1.9 e_0 + e_1) z^{-1} \\ &+ (0.9 e_0 - 1.9 e_1 + f_0) z^{-2} \\ &+ (0.9 e_1 + f_1) z^{-3} \end{aligned}$

继续匹配各项系数得到：

$1 = e_0 \cdot 1 \quad \Rightarrow \quad e_0 = 1$ $0 = e_0 (-1.9) + e_1 \cdot 1 \quad \Rightarrow \quad -1.9 \cdot 1 + e_1 = 0 \quad \Rightarrow \quad e_1 = 1.9$ $0 = 0.9 e_0 - 1.9 e_1 + f_0 \quad \Rightarrow \quad 0.9 \cdot 1 - 1.9 \cdot 1.9 + f_0 = 0$

计算得到：

$0.9 - 3.61 + f_0 = 0 \quad \Rightarrow \quad f_0 = 2.71$

继续匹配得到：

$0 = 0.9 e_1 + f_1 \quad \Rightarrow \quad 0.9 \cdot 1.9 + f_1 = 0 \quad \Rightarrow \quad f_1 = -1.71$

综上所述得到：

$E_2(z^{-1}) = 1 + 1.9 z^{-1}, \quad F_2(z^{-1}) = 2.71 - 1.71 z^{-1}$

有了这些过程我们就可以逐步得到G的数值，我们带入计算得到：

$G_1(z^{-1}) = E_1(z^{-1}) B(z^{-1}) = 1 \cdot 0.1 = 0.1$

根据系数得到：$g_1 = 0.1$，因不包含z项，输出时无延迟的。

$G_2(z^{-1}) = E_2(z^{-1}) B(z^{-1}) = (1 + 1.9 z^{-1}) \cdot 0.1 = 0.1 + 0.19 z^{-1}$

按照z的幂次得到系数为：$g_2^{(0)} = 0.1 , g_2^{(1)} = 0.19$

接下来需要构建预测方程，预测方程的表达式如下：

$\hat{y}(k+j) = \underbrace{F_j(z^{-1}) y(k)}_{\text{自由响应}} + \underbrace{G_j(z^{-1}) \Delta u(k+j-d)}_{\text{受控响应}} + \text{噪声项}$

预测方程表示未来输出$\hat{y}(k+j)$的表达式，由自由响应和受控响应组成：

我们现在有j=1和j=2时刻的所有中间变量值，我们进行预测y的值：

$\hat{y}(k+3|k) = F_3(z^{-1}) y(k) + G_3(z^{-1}) \Delta u(k+3-2) + \text{噪声项}$

我们需要继续分解j=3的Diophantine方程得到$F_3$，但为简化说明，假设利用j=1和j=2进而已计算得到：

$F_3(z^{-1}) = 3.249 - 2.439 z^{-1}$ $F_3(z^{-1}) y(k) = 3.249 y(k) - 2.439 y(k-1)$

接下来构建矩阵G，其表示未来控制增量对输出的影响其元素$ g_{i,j}$ 表示第$j$步控制增量对第$i$步输出的增益。

由于系统延迟$d=2$，控制增量 $\Delta u(k)$ 最早在第$ k+2$步影响输出。除了j=3以外都已经写出 $G_j(z^{-1})$ 的系数，这里省略步骤三的计算直接给出答案：

$G_1(z^{-1}) = 0.1$
$G_2(z^{-1}) = 0.1 + 0.19 z^{-1}$
$G_3(z^{-1}) = 0.1 + 0.19 z^{-1} + 0.171 z^{-2}$

预测时域$N_p=3$，控制时域$N_u=2$，得到矩阵为(考虑到d=2)：

$G = \begin{bmatrix} g_{3,1} & g_{3,2} \\ g_{4,1} & g_{4,2} \\ g_{5,1} & g_{5,2} \end{bmatrix} = \begin{bmatrix} 0.1 & 0 \\ 0.19 & 0.1 \\ 0.171 & 0.19 \end{bmatrix}$

其中：

$g_{3,1} = 0.1$: $\Delta u(k)$ 对 $ y(k+3) $ 的增益（延迟2步后生效）。
$ g_{4,1} = 0.19 $: $\Delta u(k)$ 的后续增益（动态特性）。
$ g_{4,2} = 0.1 $: $\Delta u(k+1)$ 对 $ y(k+4) $ 的增益。

然后我们需要构建目标函数，目标函数权衡输出跟踪精度和控制量变化，一般写作下式：

$J = \sum_{j=1}^{N_p} \left[ \hat{y}(k+d+j|k) - r(k+d+j) \right]^2 + \lambda \sum_{j=1}^{N_u} \Delta u(k+j-1)^2$

将预测方程代入，化简为矩阵形式：

$J = (\boldsymbol{G} \Delta \boldsymbol{U} + \boldsymbol{F} - \boldsymbol{R})^T (\boldsymbol{G} \Delta \boldsymbol{U} + \boldsymbol{F} - \boldsymbol{R}) + \lambda \Delta \boldsymbol{U}^T \Delta \boldsymbol{U}$

其中：

$ \Delta \boldsymbol{U} = [\Delta u(k), \Delta u(k+1)]^T $: 待优化的控制增量。
$ \boldsymbol{F} = [F_1(z^{-1}) y(k), F_2(z^{-1}) y(k), F_3(z^{-1}) y(k)]^T $: 自由响应向量。
$ \boldsymbol{R} = [r(k+3), r(k+4), r(k+5)]^T $: 参考轨迹向量。

通过对 $ \Delta \boldsymbol{U} $ 求导并令导数为零，得到最优解：

$\Delta \boldsymbol{U}^* = (\boldsymbol{G}^T \boldsymbol{G} + \lambda \boldsymbol{I})^{-1} \boldsymbol{G}^T (\boldsymbol{R} - \boldsymbol{F})$

最后我们就需要实时控制和优化了，过程非常简单，提取控制增量最优解的第一个元素：

$\Delta u(k) = \Delta \boldsymbol{U}^*[1]$

然后就可以更新控制了：

$u(k) = u(k-1) + \Delta u(k)$

自此循环下去。下面给出matlab代码：

% GPC参数设置
clear; clc;

% CARIMA模型参数
A = [1, -0.9];      % A(z^{-1}) = 1 - 0.9z^{-1}
B = [0, 0, 0.1];    % B(z^{-1}) = 0.1z^{-2}（延迟d=2）
d = 2;              % 输入到输出的延迟步数
C = [1, -1];        % C(z^{-1}) = 1 - z^{-1}

% GPC设计参数
Np = 10;            % 预测时域
Nu = 3;             % 控制时域
lambda = 0.1;       % 控制权重

% 生成参考轨迹（阶跃信号）
k_max = 50;
ref = zeros(k_max, 1);
ref(20:end) = 1;

% 初始化系统变量
y = 0;              % 当前输出
u = 0;              % 当前控制输入
y_history = zeros(k_max, 1);
u_history = zeros(k_max, 1);
DeltaU_past = zeros(d + Np - 1, 1); % 历史控制增量（覆盖延迟d=2的影响）

% 计算GPC多项式（离线步骤）
[E, F, G] = diophantine_solver(A, B, d, Np);

% 滚动优化循环
for k = 1:k_max
    % --- 预测自由响应（Free Response）---
    F_response = zeros(Np, 1);
    for j = 1:Np
        Fj = F{j};
        % 计算F_j(z^{-1}) y(k)（需历史输出y(k), y(k-1)）
        F_response(j) = Fj(1) * y;
    end
    
    % 计算历史控制增量影响 H * ΔU_past
    H = zeros(Np, length(DeltaU_past));
    for j = 1:Np
        Gj = G{j};
        for i = 1:length(DeltaU_past)
            if (j + d - i) > 0 && (j + d - i) <= length(Gj)
                H(j, i) = Gj(j + d - i);
            end
        end
    end
    H_response = H * DeltaU_past;
    
    Free_Response = F_response + H_response;
    
    % --- 构造参考轨迹 ---
    R = ref(k + d : min(k + d + Np -1, k_max)); % 对齐延迟d
    if length(R) < Np
        R = [R; repmat(ref(end), Np - length(R), 1)];
    end
    
    % --- 构建动态矩阵G（考虑延迟d=2）---
    G_matrix = zeros(Np, Nu);
    for j = 1:Np
        Gj = G{j};
        for m = 1:Nu
            step = j + d - m; % 控制增量 Δu(k+m-1) 在 j+d 步生效
            if step > 0 && step <= length(Gj)
                G_matrix(j, m) = Gj(step);
            end
        end
    end
    
    % --- 计算最优控制增量 ---
    DeltaU = (G_matrix' * G_matrix + lambda * eye(Nu)) \ (G_matrix' * (R - Free_Response));
    delta_u = DeltaU(1); % 取首步控制增量
    
    % --- 施加控制并更新系统 ---
    u_new = u + delta_u;
    % 系统仿真（真实模型）
    y = 0.9 * y + 0.1 * u_history(max(k-2,1)) + (randn() * 0.01); % 注意u的延迟d=2
    
    % --- 更新历史数据 ---
    DeltaU_past = [delta_u; DeltaU_past(1:end-1)]; % 维护历史控制增量
    u = u_new;
    
    % --- 记录结果 ---
    y_history(k) = y;
    u_history(k) = u;
end

% 可视化
figure;
subplot(2,1,1);
plot(1:k_max, y_history, 'b-', 1:k_max, ref, 'r--');
xlabel('Time Step'); ylabel('Output'); 
legend('Actual', 'Reference'); title('GPC Control (d=2)');
grid on;

subplot(2,1,2);
stairs(1:k_max, u_history, 'm-', 'LineWidth', 1.5); % 使用实线绘制
xlabel('Time Step'); ylabel('Control Input');
title('Control Signal');
grid on;


% --- Diophantine方程求解函数 ---
function [E, F, G] = diophantine_solver(A, B, d, Np)
    % 输入参数:
    %   A: 多项式A(z^{-1})的系数（行向量，如[1 -0.9]）
    %   B: 多项式B(z^{-1})的系数（带延迟，如[0 0 0.1]表示0.1z^{-2}）
    %   d: 输入到输出的延迟步数（此处d=2）
    %   Np: 预测时域（预测步数）
    % 输出参数:
    %   E: 元胞数组，E{j}对应E_j(z^{-1})的系数
    %   F: 元胞数组，F{j}对应F_j(z^{-1})的系数
    %   G: 元胞数组，G{j}对应G_j(z^{-1}) = E_j(z^{-1})*B(z^{-1})的系数

    % 初始化输出
    E = cell(Np, 1);
    F = cell(Np, 1);
    G = cell(Np, 1);

    % 计算Δ(z^{-1}) = 1 - z^{-1}的系数
    Delta = [1, -1];  % Δ(z^{-1}) = 1 - z^{-1}

    % 计算AΔ(z^{-1}) = A(z^{-1})*Δ(z^{-1})的系数
    A_Delta = conv(A, Delta);  % 多项式乘法

    % 递推求解Diophantine方程: 1 = E_j*AΔ + z^{-j}F_j
    for j = 1:Np
        % 计算E_j的阶数（j-1阶）
        E_degree = j - 1;
        % 初始化E_j的系数（待求解）
        E_j = zeros(1, E_degree + 1);

        % 构建系数方程组:
        % E_j*AΔ + z^{-j}F_j = 1
        % 分别匹配z^0, z^{-1}, ..., z^{-(nAΔ + E_degree -1)}的系数
        coeff_matrix = zeros(E_degree + length(A_Delta), E_degree + 1 + length(A_Delta) - 1);
        
        for k = 0:E_degree + length(A_Delta) - 1
            % E_j*AΔ的系数
            for m = max(0, k - (length(A_Delta)-1)):min(E_degree, k)
                if (m <= E_degree) && (k - m <= length(A_Delta)-1)
                    coeff_matrix(k+1, m+1) = A_Delta(k - m + 1);
                end
            end
            
            % z^{-j}F_j的系数（F_j的阶数为nAΔ -1）
            if k >= j && k - j <= length(A_Delta) - 1
                coeff_matrix(k+1, E_degree + 1 + (k - j)) = 1;
            end
        end

        % 右端向量（z^0的系数为1，其余为0）
        rhs = zeros(E_degree + length(A_Delta), 1);
        rhs(1) = 1;  % z^0的系数为1

        % 求解方程组
        solution = coeff_matrix \ rhs;
        
        % 提取E_j和F_j的系数
        E_j = solution(1:E_degree + 1)';
        F_j = solution(E_degree + 2:end)';

        % 计算G_j(z^{-1}) = E_j(z^{-1})*B(z^{-1})
        G_j = conv(E_j, B);

        % 存储结果
        E{j} = E_j;
        F{j} = F_j;
        G{j} = G_j;
    end
end

机器人学

#C++ #数学 #机器人学

机器人学基础——控制方法

https://blog.minloha.cn/posts/10071892ddae2f2025020740.html

作者

Minloha

发布于

2025年2月7日

更新于

2025年2月9日

许可协议

新年规划与杂谈下一篇