机器人学基础[控制章]——其他控制方法

说明

在本期开始前我必须要说一下，我之所以不按照控制器的线性与非线性划分，是因为非线性控制其实是一个大类，就比如反馈线性化、极点配置法、李雅普诺夫稳定、模型控制等等，都包含了非线性控制的思路，甚至于模糊控制和滑膜也是如此，所以无法按照一般的分类去看待控制器，只能利用控制特点进行区分，所以本期博客介绍两类极强的、范围极广的控制即：鲁棒控制和智能控制。

鲁棒控制将会写$H\infty$控制、$\mu$综合、滑模控制，智能控制将会说模糊控制、优化控制器以及强化学习控制。

本期内容我们会引入广义坐标的概念，我们可以指定一种状态方程即：

$x_{t+1}=Ax_t$

存在一种时序上的递推，我们假设A是单位矩阵，我们可以写成表达式：

$\begin{cases} \dot{x}_1 = x_0 \\ \dot{x}_2 = x_1 \\ \vdots \\ \dot{x}_n = x_{n-1}\\ \end{cases}$

类似这种以初始状态的递推过程。所以其下角标可以理解为前一个变量的导数。

鲁棒控制

提到鲁棒控制不得不说一下鲁棒性（Robustness），它指的是一类在参数变化、建模误差、外界扰动或传感器噪声等不确定性下，仍能维持预期性能的能力。（我也不知道为什么要音译，不如叫抗干扰性）

这些不确定性大概可以分为两类：

结构化不确定性：系统模型参数的变化范围已知（如机械臂关节质量±10%）
非结构化不确定性：高频未建模动态、未知干扰（如风扰动对无人机的影响）

所以我们需要规避这两种不确定性进行控制，我们必须保证控制的稳定性和对突发情况的适应性。这些都是传统的、单纯的PID无法做到的事情：

特性	经典控制（如PID）	鲁棒控制
模型依赖	依赖精确数学模型	允许模型存在不确定性
抗干扰能力	依赖实时反馈补偿	提前设计时考虑干扰范围
适用范围	确定性系统	高不确定性复杂系统
典型方法	频域设计、根轨迹法	$H\infty$控制、$\mu$综合、滑模控制

那么我们就可以开始本期博客

$H\infty$控制

又叫H无穷控制，关键在于定义了一种新范数（H无穷范数），这种范数并非平时常用的诱导范数，H范数是定义在频域上的而L范数是时域的，对于控制而言，我们可以在频域控制自然是最稳定的（因为我们可以找出最有可能的情况从而进行反馈），具体对比两组范数见下表：

特性	$H\infty$范数	$\mathcal{L}_\infty$诱导范数
定义域	频域（频率响应矩阵的最大奇异值）	时域（输入输出信号的无穷范数）
物理意义	系统在频域上的最大增益	系统在时域上的最大幅值响应
计算方法	通过传递函数矩阵的频率响应计算奇异值	通过脉冲响应或阶跃响应的时域积分或幅值计算

首先我们定义一种状态空间表达式：

$\begin{cases} \dot{x} = A x + B_1 w + B_2 u \\ z = C_1 x + D_{11} w + D_{12} u \\ y = C_2 x + D_{21} w \end{cases}$

其中：

x 是状态向量，
u 是控制输入，
w 是外部干扰或不确定性，
z 是被控输出（性能指标），
y 是测量输出。

然后我们引入H无穷范数，计算公式如下：

$\|G\|_{\infty} = \sup_{\omega} \bar{\sigma}(G(j\omega))$

含义为频域响应函数G的最大奇异值，归根结底我们还是需要设置反馈矩阵K，由李氏稳定判据，我们需要让输出误差在一定的范围内在可以断定其稳定：

$\|T_{zw}\|_{\infty} < \gamma$

其中 $\gamma$ 是一个给定的性能指标。而T就是闭环系统的传递函数。

类似LQR，我们同样需要设定一个K用于反馈控制，我们可以求解一个Riccati方程进行设计：

$A^T X + X A + X (B_1 B_1^T - \gamma^{-2} B_2 B_2^T) X + C_1^T C_1 = 0$

而反馈增益矩阵K可以写作：

$K = -B_2^T X$

接下来只需要进行求解即可，通过求解以下线性矩阵不等式来设计控制器：

$\begin{bmatrix} A X + X A^T + B_1 B_1^T & X C_1^T \\ C_1 X & -\gamma I \end{bmatrix} < 0$

求解这个方程即可，我们看一下matlab代码：

% 定义系统矩阵
A = [0 1; -1 -0.5];
B1 = [0; 1];
B2 = [0; 1];
C1 = [1 0];
D11 = 0;
D12 = 0;
C2 = [1 0];
D21 = 0;

% 构建状态空间模型
P = ss(A, [B1 B2], [C1; C2], [D11 D12; D21 0]);

% 设计H∞控制器
[K, CL, gamma] = hinfsyn(P, 1, 1); % 1个控制输入，1个测量输出

% 显示控制器和闭环系统
disp('H∞控制器 K:');
disp(K);
disp('闭环系统 CL:');
disp(CL);
disp('H∞范数 gamma:');
disp(gamma);

% 仿真闭环系统
t = 0:0.01:10;
w = 0.1 * sin(t); % 外部干扰
[y, t, x] = lsim(CL, w, t);

% 可视化结果
figure;
plot(t, y(:,1), 'b-', t, w, 'r--');
xlabel('Time'); ylabel('Output');
legend('Output z', 'Disturbance w');
title('H∞ Control Response');
grid on;

输出为：

H∞控制器 K: [-3.1288e+05 -841.8763]
闭环系统 CL: ss - [1 0 0 0]
H∞范数 gamma:
   8.4383e-06

从图上可以看到，无论如何增加干扰项w，输出z永远稳定。

$\mu$综合

我们需要给出一种结构不确定的控制，即不确定性以特定的结构和形式出现，我们需要一种叫$\mu$分析的办法。

我们的$\mu$其实是一种结构化的奇异值，我们可以用下面的方法计算出来：

$\mu_{\Delta}(M) = \frac{1}{\min\{\sigma(\Delta) | \det(I - M\Delta) = 0\}}$

$M$ 是系统的传递函数矩阵，
$\Delta$ 是描述不确定性的矩阵。

我们需要设置一个控制器，使得闭环系统在所有允许的不确定性下能够满足如下的要求：

1、稳健性：所有不确定的情况下都是稳定的
2、性能：所有不确定的情况下都能满足性能要求

既然如此，我们需要进行如下的设计步骤：

1、建立广义系统，包括对模型的标准描述和不确定性描述
2、定义不确定性矩阵，这里一般采用块对角矩阵描述，诸如参数不确定性和未建模动态等。（个人感觉是表达性更强的隶属度函数）
3、设置$\mu$综合控制器，通过迭代优化法使得闭环系统的$\mu$最小
4、最后可以对系统进行分析

下面是Matlab代码仿真：

clc; clear; close all;

%% 建立广义系统
s = tf('s');
G_nom = 1 / (s + 1);       
delta = ultidyn('delta', [1 1]);  
G_uncertain = G_nom * (1 + 0.2 * delta);  

%% 不确定性矩阵
W1 = makeweight(10, 1, 0.1);   
W2 = makeweight(0.1, 10, 10);  

%% 构建受控对象
systemnames = 'G_uncertain W1 W2';
inputvar = '[r; u]';
outputvar = '[W1; W2; r - G_uncertain]';
input_to_G_uncertain = '[u]';
input_to_W1 = '[r - G_uncertain]';
input_to_W2 = '[u]';
sysoutname = 'P';
cleanupsysic = 'yes';
sysic;

%% μ综合控制器设计
nmeas = 1;  
ncont = 1;  
[Kmu, CL, bnd, info] = dksyn(P, nmeas, ncont);
disp('μ综合上界（最小值）：');
disp(bnd(end));

%%提取性能函数
L = G_nom * Kmu;      
S = feedback(1, L);    
T = feedback(L, 1);    

%% 闭环系统阶跃响应
figure;
step(CL, 5);
title('图1：闭环系统阶跃响应');
xlabel('时间 (秒)');
ylabel('输出 y(t)');
legend('闭环响应');
grid on;
text(1.5, 0.8, '响应时间、超调等性能可视', 'FontSize', 10);

%% 灵敏度函数 S vs 1/W1
figure;
bodemag(S, inv(W1), {1e-2, 1e2});
title('图2：灵敏度函数 S 与 1/W1 对比');
xlabel('频率 (rad/s)');
ylabel('增益 (dB)');
legend('|S|', '1/W1（期望上限）', 'Location', 'SouthWest');
grid on;
text(3, 10, '目标：|S| 全部低于 1/W1', 'FontSize', 10);

%% 互补灵敏度函数 T vs 1/W2
figure;
bodemag(T, inv(W2), {1e-2, 1e2});
title('图3：互补灵敏度函数 T 与 1/W2 对比');
xlabel('频率 (rad/s)');
ylabel('增益 (dB)');
legend('|T|', '1/W2（控制器增益上限）', 'Location', 'SouthEast');
grid on;
text(1, 0, '目标：高频段 |T| < 1/W2', 'FontSize', 10);

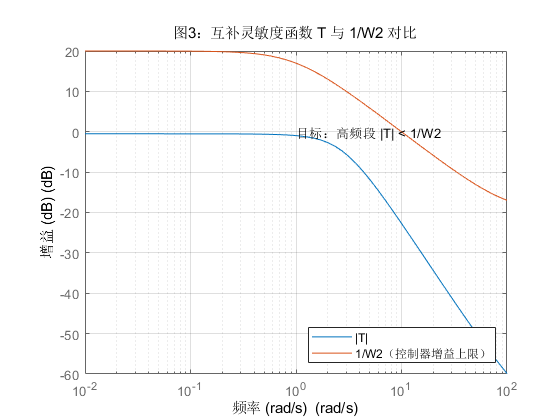
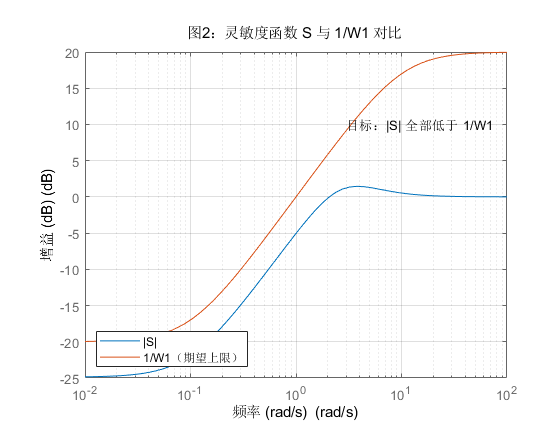
如图所示，其效果非常明显，这样我们完成了对不确定系统的稳健性控制。

非线性控制

在现代控制理论中也对非线性控制进行了介绍，其方法较为古老。比如反馈线性化和极点配置法等，其思路都是构建反馈矩阵。这一部分介绍反步法和滑模控制法，用于补充较为高级的非线性控制器，并且适合严格的反馈系统。

反步法

反步法是一种递归设计非线性控制器的方法，通过Lyapunov函数和虚拟控制律，将系统分解为多个子系统，逐步稳定每个子系统。我们假设一个反馈系统，我们可以写作：

$\begin{cases} \dot{x}_1 = f_1(x_1) + g_1(x_1)x_2 \\ \dot{x}_2 = f_2(x_1, x_2) + g_2(x_1, x_2)x_3 \\ \vdots \\ \dot{x}_n = f_n(x_1, x_2, \dots, x_n) + g_n(x_1, x_2, \dots, x_n)u \end{cases}$

其中：

$x_i$ 是系统状态。
$u$ 是控制输入。
$f_i$ 和 $g_i$是已知的非线性函数。

我们的关键分为三步：1、分解系统2、设计虚拟控制律3、构造Lyapunov函数。

首先需要定义一个误差，我们通过如下的方式定义：

$z_1 = x_1 - x_{1d}$

其中$ x_{1d}$为期望值，我们给误差提供一个比例，制定负反馈控制率：

$\alpha_1 = -k_1 z_1$

其中k为设计参数，且$k_1>0$

其次我们构建一个Lyapunov函数，我们可以用标准的二次方程：

$V_1 = \frac{1}{2} z_1^2$

我们对其求导，可以得到：

$\dot{V}_1 = z_1 \dot{z}_1 = z_1 (f_1(x_1) + g_1(x_1)x_2 - \dot{x}_{1d})$

其中的$x_2$为$x_1$的导数，其可以看作为广义坐标的一种表达方式（参考第一章机器人学基础——控制理论）我们可以通过虚拟控制率去保证Lyapunov导数小于0。

接下来我们需要对其进行递归设计，我们可以定义第二个误差：

$z_2 = x_2 - \alpha_1$

我们就可以更新Lyapunov函数：

$V_2 = V_1 + \frac{1}{2} z_2^2$

以此方法我们最终可以得出最终的控制率，因此我们实现matlab进行仿真：

function backstepping()
    % 系统参数
    x1 = 1; x2 = 0; % 初始状态
    x1d = 9; % 期望值
    k1 = 1; k2 = 2; % 控制增益

    % 仿真参数
    dt = 0.01; % 时间步长
    T = 10; % 仿真时间
    t = 0:dt:T; % 时间向量

    % 初始化状态
    x1_history = zeros(size(t));
    x2_history = zeros(size(t));
    u_history = zeros(size(t));

    % 仿真循环
    for i = 1:length(t)
        % 误差和虚拟控制律
        z1 = x1 - x1d;
        alpha1 = -k1 * z1;

        % 控制律
        z2 = x2 - alpha1;
        u = -k2 * z2 - z1;

        % 系统动态
        dx1 = x2;
        dx2 = u;

        % 更新状态
        x1 = x1 + dx1 * dt;
        x2 = x2 + dx2 * dt;

        % 记录状态和控制输入
        x1_history(i) = x1;
        x2_history(i) = x2;
        u_history(i) = u;
    end

    % 绘图
    figure;
    subplot(3, 1, 1);
    plot(t, x1_history, 'b', 'LineWidth', 1.5);
    xlabel('Time (s)');
    ylabel('x_1');
    title('State x_1');

    subplot(3, 1, 2);
    plot(t, x2_history, 'r', 'LineWidth', 1.5);
    xlabel('Time (s)');
    ylabel('x_2');
    title('State x_2');

    subplot(3, 1, 3);
    plot(t, u_history, 'g', 'LineWidth', 1.5);
    xlabel('Time (s)');
    ylabel('u');
    title('Control Input');
end

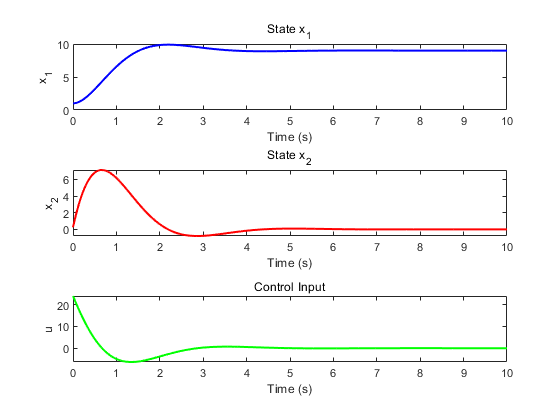
我们可以看到设定了期望值后可以非常快速的收敛，通过两个控制增益非常快速的收敛。

滑模控制器

滑模控制是非常强大的非线性控制方法，对不确定性和扰动的系统有极强的控制效果，核心思想是通过控制滑动的模态使得系统在有限步数内收敛到滑动模态并保持稳定。与反步法类似，我们也需要设定控制律，正如下面的抽象表述：

$u = u_{eq} + u_{sw}$

等效控制$u_{eq}$用于保持系统在滑动面上。
切换控制$u_{sw}$用于驱动态到滑动面。

而u作为系统的输入控制，我们可以发现其对不确定性和外部扰动具有强稳健性。

既然是滑模控制，我们首先假设一个系统：

$\dot{x} = f(x) + g(x)u + d(t)$

其中的d(t)为随机扰动，表示为一个时间函数，我们可以写出实际与期望的误差：

$e=x-x_d$

其中的$x_d$为期望值，我们就可以设定滑模面：

$s=\dot e+\lambda e$

其中的$\lambda>0$是我们的设计参数。接下来设定等效控制：

$u_{eq} = g^{-1}(x) (-\dot{f}(x) + \ddot{x}_d - \lambda \dot{e})$

以及切换控制律：

$u_{sw} = -K \, \text{sign}(s)$

其中的K是整体的设计参数，然后我们构建Lyapunov函数：

$V = \frac{1}{2} s^2$

同时满足李氏稳定判据即有界性：

$\dot{V} \leq -\eta |s|$

其中$\eta > 0$。然后我们假设一个二阶系统，我们写作：

$\begin{cases} \dot{x}_1 = x_2 \\ \dot{x}_2 = u + d(t) \end{cases}$

我们需要设定控制律u，使得$x_1$可以跟踪预设期望值，并抑制扰动。

重复上述步骤，首先定义误差：

$e = x_1 - x_{1d}$

设计滑动面：

$s = \dot{e} + \lambda e = x_2 - \dot{x}_{1d} + \lambda e$

这样我们就得到等效控制和切换控制：

$u_{eq} = -x_2 + \ddot{x}_{1d} - \lambda \dot{e}$ $u_{sw} = -K \text{sign}(s)$

同样的，李氏函数为：

$V = \frac{1}{2} s^2$

function SMC()
    % 系统参数
    x1 = 1; x2 = 0; % 初始状态
    x1d = 10; % 期望值
    lambda = 1; K = 5; % 控制参数

    % 仿真参数
    dt = 0.01; % 时间步长
    T = 10; % 仿真时间
    t = 0:dt:T; % 时间向量

    % 初始化状态
    x1_history = zeros(size(t));
    x2_history = zeros(size(t));
    u_history = zeros(size(t));

    % 仿真循环
    for i = 1:length(t)
        % 定义误差和滑动面
        e = x1 - x1d;
        s = x2 + lambda * e;

        % 等效控制
        u_eq = -x2 - lambda * x2;

        % 切换控制
        u_sw = -K * sign(s);

        % 控制律
        u = u_eq + u_sw;

        % 系统动态（假设扰动 d(t) = 0.1 * sin(t)）
        d = 0.1 * sin(t(i));
        dx1 = x2;
        dx2 = u + d;

        % 更新状态
        x1 = x1 + dx1 * dt;
        x2 = x2 + dx2 * dt;

        % 记录状态和控制输入
        x1_history(i) = x1;
        x2_history(i) = x2;
        u_history(i) = u;
    end

    % 绘图
    figure;
    subplot(3, 1, 1);
    plot(t, x1_history, 'b', 'LineWidth', 1.5);
    xlabel('Time (s)');
    ylabel('x_1');
    title('State x_1');

    subplot(3, 1, 2);
    plot(t, x2_history, 'r', 'LineWidth', 1.5);
    xlabel('Time (s)');
    ylabel('x_2');
    title('State x_2');

    subplot(3, 1, 3);
    plot(t, u_history, 'g', 'LineWidth', 1.5);
    xlabel('Time (s)');
    ylabel('u');
    title('Control Input');
end

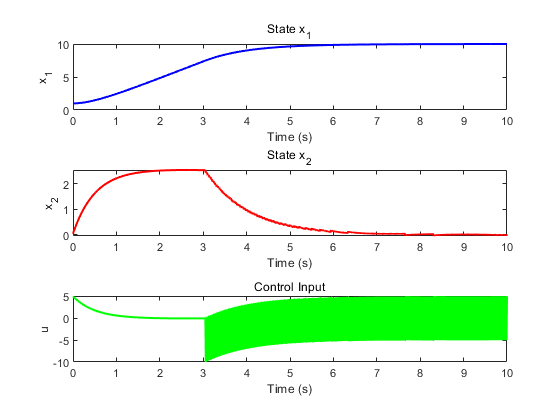
可以看到其反应速度一般快，但是对外部的正弦周期性扰动控制的非常好，甚至是稳健的。

智能控制

提到智能控制，首先想到的就是神经网络控制，但是这是优化较为费时的优化控制器，针对一些特殊的场合是十分受用的。但是对于一般情况我们需要一些基础的控制器，比如pid。

模糊PID

模糊通常意味不清晰，在日常生活中我们通常会对一些事物进行模糊的描述比如：沙发上白色的手机而非使用我的手机，亦或者树上红色的苹果。这些都有共同点就是用一系列约束条件去约束一个事物，每一个约束多值连续的映射，而这些映射最终存在交集即我们的目标。对于一般的控制器，我们也可以这样去修改，如果是一个模糊系统，通常包含四部分：

模糊化
规则
内在推理
去模糊化

其中的模糊化大有话说，我们通过经验指定规则，利用隶属度函数描述交给控制器，通过合适的规则即可让控制器收敛。对于我们的PID控制器，我们也可以对其模糊化。

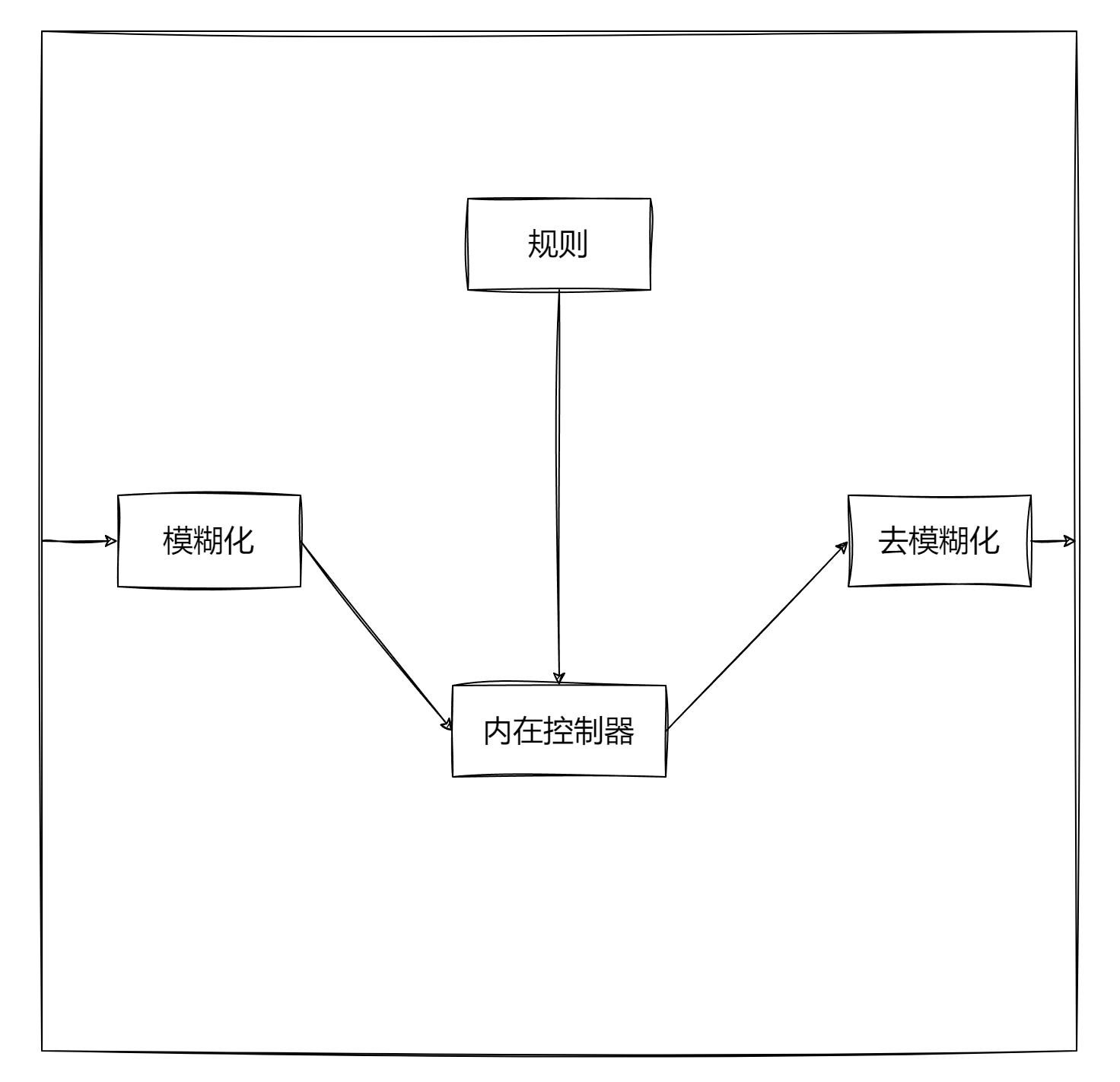
我们以模糊PID为，我们通过一系列描述函数进行动态系数变换，包括如下：

名称	作用
NB	负方向的大数
NM	负方向的中等数
NS	负方向的小数
ZO	0位的数
PS	正方向的小数
PM	正方向的中等数
PB	正方向的大数

我们通过这些函数既可以对PID进行动态变化。有一句描述非常正确的话处理pid：

IF e is NB AND de/dt is NB THEN ΔKp is PB, ΔKi is NB, ΔKd is PS

理解为：如果误差和误差变化率是NB的，则Kp是PB的，Ki是NB的，Kd是PS的，也就是Kp正大方向，Ki负大方向，Kd正小方向。

动态参数如下：

$K_p=K_{p0}+\Delta K_p,K_i=K_{i0}+\Delta K_i,K_d=K_{d0}+\Delta K_d$

对模糊PID我们需要利用隶属度动态调节PID，初始状态需要一个合适的PID系数，再通过模糊用于提高鲁棒性。模糊PID的代码在Github有大佬写好了，我就直接给出github链接了。

1	`https://github.com/FlameAlpha/fuzzy-pid.git`

隶属度函数包含很多形状，这些都是对信息过度进行不同强度的描述，代码给出了：

隶属度函数 Membership function
- 高斯隶属度函数 Gaussian membership function
- 广义钟形隶属度函数 Generalized bell-shaped membership function
- S形隶属度函数 Sigmoidal membership function
- 梯形隶属度函数 Trapezoidal membership function
- 三角形隶属度函数 Triangular membership function
- Z形隶属度函数 Z-shaped membership function
模糊算子 Fuzzy operator
- 并算子 Union operator
- 交算子 Intersection operator
- 平衡算子 Equilibrium operator
中心平均解模糊器 Mean of centers defuzzifier

按照大佬的C语言实例可以快速部署这个模糊pid到自己的C语言平台，我用Matlab简单仿真一下就好。

%% 高精度模糊PID控制器（修正版）
clear; clc; close all;

% 1. 增强型模糊推理系统设计
fis = newfis('precision_fuzzy_pid', 'mamdani');

% 输入1：误差e（7个隶属函数）
fis = addvar(fis, 'input', 'e', [-2 2]);
fis = addmf(fis, 'input', 1, 'NB', 'gaussmf', [0.3 -2]);
fis = addmf(fis, 'input', 1, 'NM', 'gaussmf', [0.3 -1]);
fis = addmf(fis, 'input', 1, 'NS', 'gaussmf', [0.2 -0.5]);
fis = addmf(fis, 'input', 1, 'ZO', 'gaussmf', [0.1 0]);
fis = addmf(fis, 'input', 1, 'PS', 'gaussmf', [0.2 0.5]);
fis = addmf(fis, 'input', 1, 'PM', 'gaussmf', [0.3 1]);
fis = addmf(fis, 'input', 1, 'PB', 'gaussmf', [0.3 2]);

% 输入2：误差变化率de/dt（3个隶属函数）
fis = addvar(fis, 'input', 'de_dt', [-0.5 0.5]);
fis = addmf(fis, 'input', 2, 'N', 'gaussmf', [0.1 -0.5]);
fis = addmf(fis, 'input', 2, 'Z', 'gaussmf', [0.05 0]);
fis = addmf(fis, 'input', 2, 'P', 'gaussmf', [0.1 0.5]);

% 输出：积分项调节（主要消除稳态误差）
fis = addvar(fis, 'output', 'delta_Ki', [-0.5 0.5]);
fis = addmf(fis, 'output', 1, 'NB', 'gaussmf', [0.1 -0.5]);
fis = addmf(fis, 'output', 1, 'NS', 'gaussmf', [0.05 -0.2]);
fis = addmf(fis, 'output', 1, 'ZO', 'gaussmf', [0.02 0]);
fis = addmf(fis, 'output', 1, 'PS', 'gaussmf', [0.05 0.2]);
fis = addmf(fis, 'output', 1, 'PB', 'gaussmf', [0.1 0.5]);

% 2. 精准调节规则库
rules = [
    1 1 1 1 1;  2 1 1 1 1;  3 1 2 1 1;  4 1 3 1 1;
    5 1 4 1 1;  6 1 5 1 1;  7 1 5 1 1;
    1 2 1 1 1;  2 2 2 1 1;  3 2 2 1 1;
    4 2 3 1 1;  5 2 4 1 1;  6 2 5 1 1;
    7 2 5 1 1;  1 3 5 1 1;  2 3 5 1 1;
    3 3 4 1 1;  4 3 3 1 1;  5 3 2 1 1;
    6 3 1 1 1;  7 3 1 1 1;
];
fis = addrule(fis, rules);

% 3. 仿真设置
dt = 0.01;
t = 0:dt:15;
r = ones(size(t));
y = zeros(size(t));
e = zeros(size(t));

% 初始参数
Kp = 3.0;
Ki = 0.5;
Kd = 0.3;

% 系统定义（状态空间形式更稳定）
A = [0 1; -20 -10];
B = [0; 1];
C = [1 0];
D = 0;
sys = ss(A,B,C,D);


% 4. 噪声生成（高斯白噪声+周期性干扰）
rng(1); % 固定随机种子
noise_amp = 0.1; % 噪声幅值
noise = noise_amp * randn(size(t)); 
periodic_noise = 0.05*sin(2*pi*0.5*t); % 0.5Hz低频干扰
disturbance = noise + periodic_noise;

% 4. 改进的控制循环（修复lsim问题）
x = [0; 0];  % 初始状态
integral = 0;
integral_max = 5;
u_prev = 0;

for k = 2:length(t)
    % 误差计算
    e(k) = r(k) - y(k-1);
    
    % 模糊推理
    norm_e = min(max(e(k)/2, -1), 1);
    norm_de = min(max((e(k)-e(k-1))/dt/0.5, -1), 1);
    delta_Ki = evalfis(fis, [norm_e, norm_de]);
    
    % 动态调整Ki
    Ki = max(0.1, Ki + 0.02*delta_Ki);
    
    % 抗饱和积分
    integral = integral + e(k)*dt;
    integral = sign(integral)*min(abs(integral), integral_max);
    
    % PID计算
    P = Kp * e(k);
    I = Ki * integral;
    D = Kd * (e(k)-e(k-1))/dt;
    % 整合输出并加入控制噪声
    u = P + I + D + 0.01 * randn();
    u = max(min(u, 50), -50);  % 输出限幅
    
    % 状态更新（使用ode45提高精度）
    [~,X] = ode45(@(t,x) A*x + B*u, [t(k-1) t(k)], x(:,k-1));
    x(:,k) = X(end,:)';
    y(k) = C*x(:,k);
end

% 5. 专业可视化
figure('Position', [100,100,1000,600])

% 响应曲线
subplot(3,1,1);
plot(t, r, 'k--', t, y, 'b', 'LineWidth', 1.5);
title(['Fuzzy PID Response (SSE: ', num2str(mean(abs(e(end-100:end))), '%.4f'), ...
      ', Kp=', num2str(Kp,2), ', Ki=', num2str(Ki,2), ', Kd=', num2str(Kd,2), ')']);
xlabel('Time (s)'); ylabel('Output');
legend('Reference', 'Output', 'Location', 'southeast');
grid on;
ylim([0 1.2]);

% 误差曲线
subplot(3,1,2);
plot(t, e, 'r', 'LineWidth', 1);
title('Error Evolution');
xlabel('Time (s)'); ylabel('Error');
grid on;
ylim([-1 1]);

% 积分项变化
subplot(3,1,3);
plot(t, disturbance, 'm', t, 0.01*randn(size(t)), 'c:', 'LineWidth', 1.2);
title('Noise Input Analysis');
xlabel('Time (s)'); ylabel('Amplitude');
legend('System Disturbance', 'Measurement Noise', 'Location', 'northeast');
grid on;

% 打印性能指标
rise_time = t(find(y>=0.9*r(end), 1)) - t(find(y>=0.1*r(end), 1));
overshoot = (max(y)-r(end))/r(end)*100;
fprintf('Performance Metrics:\n');
fprintf('Rise Time: %.3f s\n', rise_time);
fprintf('Overshoot: %.2f%%\n', overshoot);
fprintf('Steady-state Error: %.6f\n', mean(abs(e(end-100:end))));

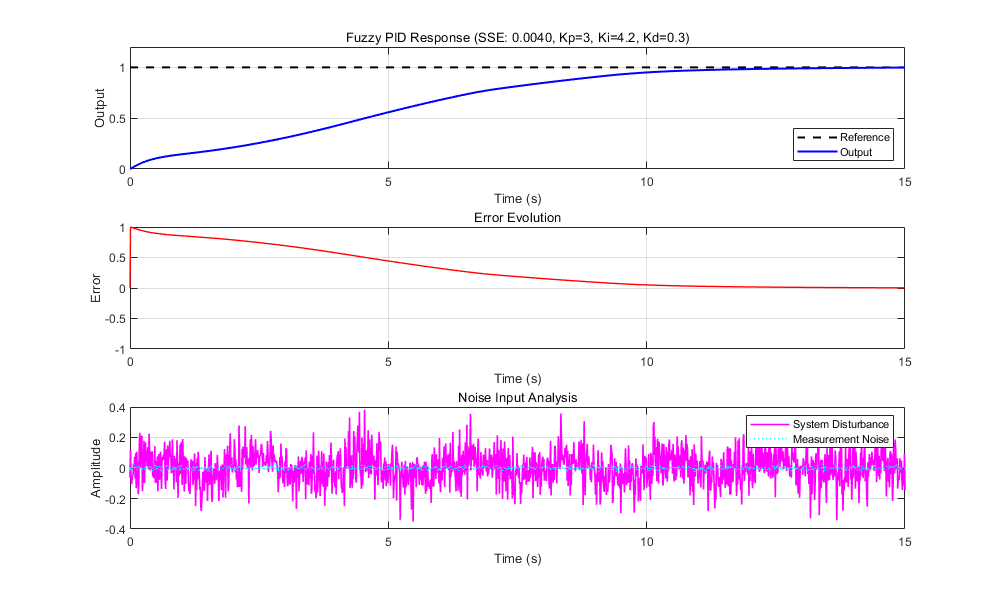
可以看出在给定一个高斯噪声的情况下，PID依然可以稳定的输出，对于这个传递函数，噪声会被放大很多很多，但是依然适应住了，所以模糊PID的鲁棒性要远远高于纯粹的PID。

遗传算法优化控制

在模糊控制后就是GA控制，这是一种模拟自然选择机制的优化算法，适合复杂的非线性多极值函数优化问题（一般的数值优化只能找到一个极值），对于GA利用类似DNA的过程进行基因的选择、交叉、变异等操作迭代出最优解。

我们可以写成下面的过程：

初始化种群：随机生成一组初始解，假设其完美
适应度评估：计算每个个体的性能指标（也就是衡量被优化对象好坏的指标）
选择：保留高适应度个体（轮盘赌、锦标赛选择等。就是随机杀死一些个体）。
交叉：交换部分基因，生成新个体。
假设个体 A: [a1, a2, a3, a4]，个体 B: [b1, b2, b3, b4]
交叉后可能变成 [a1, b2, a3, b4]、[b1, a2, b3, a4]等。
变异：随机修改某些基因，增加多样性。
随机对个体的某个基因（变量）做小范围扰动，避免陷入局部最优。
比如将某个变量加上一个小随机数 x_i = x_i + randn() * σ
替换/进化：把交叉和变异后的个体组成新的种群，继续下一代进化。回到第2步
终止条件：达到最大迭代次数或适应度收敛。

我们以PID为GA的优化对象，我们首先需要制定其性能指标，一般都是以积分项进行的，同时还有超调量的控制。我们首先制定误差的时间积分：

$IAE=\int_0^T|e(t)|dt$

然后给出时间平方的积分误差：

$ITAE=\int_0^Tte^2(t)dt$

我们写出matlab代码：

%% 遗传算法优化PID控制 - 最终修正版
clear; clc; close all;

% 步骤1：定义被控系统
s = tf('s');
sys = 1 / (s^2 + 10*s + 20);  % 传递函数：1/(s² + 10s + 20)
t = 0:0.01:5;                 % 仿真时间
r = ones(size(t));            % 参考信号（单位阶跃）

% 步骤2：遗传算法配置
options = optimoptions('ga',...
    'PopulationSize', 30, ...
    'MaxGenerations', 50, ...
    'CrossoverFraction', 0.7, ...
    'MutationFcn', {@mutationuniform, 0.1}, ...
    'SelectionFcn', 'selectionroulette', ...
    'Display', 'iter', ...
    'UseVectorized', false);

% 参数范围：Kp ∈ [0.1,5], Ki ∈ [0.1,3], Kd ∈ [0.1,1]
lb = [0.1, 0.1, 0.1];
ub = [5, 3, 1];

% 步骤3：运行遗传算法优化
rng(1);  % 固定随机种子
[best_K, best_fitness] = ga(@pid_fitness, 3, [], [], [], [], lb, ub, [], options);
fprintf('优化结果:\n Kp = %.4f\n Ki = %.4f\n Kd = %.4f\n', best_K);

% 步骤4：仿真对比
Kp0 = 1.0; Ki0 = 0.5; Kd0 = 0.2;  % 初始PID

% 确保优化参数在范围内
Kp_opt = max(lb(1), min(ub(1), best_K(1)));
Ki_opt = max(lb(2), min(ub(2), best_K(2)));
Kd_opt = max(lb(3), min(ub(3), best_K(3)));

% 仿真响应（强制列向量输出）
[y0, t] = step(feedback(pid(Kp0,Ki0,Kd0)*sys, 1), t);
[y0, t] = deal(y0(:), t(:));  % 确保列向量
[y_opt, ~] = step(feedback(pid(Kp_opt,Ki_opt,Kd_opt)*sys, 1), t);
y_opt = y_opt(:);  % 确保列向量

% 步骤5：计算性能指标（强制标量输出）
ise0 = sum((r(:) - y0).^2);
ise_opt = sum((r(:) - y_opt).^2);
overshoot0 = max(0, (max(y0) - 1) * 100);
overshoot_opt = max(0, (max(y_opt) - 1) * 100);

% 验证标量结果
if ~isscalar(ise0) || ~isscalar(ise_opt) || ~isscalar(overshoot0) || ~isscalar(overshoot_opt)
    error('性能指标计算错误：结果必须为标量值');
end

% 步骤6：绘制结果
figure('Position', [100,100,900,400])

% 阶跃响应对比
subplot(1,2,1)
plot(t, r, 'k--', t, y0, 'b', t, y_opt, 'r', 'LineWidth', 1.5)
xlabel('时间 (s)'); ylabel('输出');
title('阶跃响应对比');
legend('参考', '初始PID', '优化PID');
grid on;

% 性能指标对比（修正后的绘图方式）
subplot(1,2,2)
metrics = [ise0, ise_opt; overshoot0, overshoot_opt];
bar(metrics)
set(gca, 'XTickLabel', {'ISE', '超调量 (%)'});
ylabel('数值');
legend('初始PID', '优化PID', 'Location', 'northoutside');
title('性能指标对比');
grid on;

% 添加数值标签
for i = 1:size(metrics,1)
    for j = 1:size(metrics,2)
        text(j, metrics(i,j), sprintf('%.3f', metrics(i,j)),...
            'VerticalAlignment', 'bottom', 'HorizontalAlignment', 'center');
    end
end

% 适应度函数定义
function fitness = pid_fitness(K)
    persistent sys t r
    if isempty(sys)
        sys = tf(1, [1, 10, 20]);
        t = 0:0.01:5;
        r = ones(size(t));
    end
    
    K = abs(K);  % 确保参数为正
    
    % 创建PID控制器
    controller = pid(K(1), K(2), K(3));
    
    try
        [y, ~] = step(feedback(controller*sys, 1), t);
        y = y(:);  % 确保列向量
        
        % 计算ISE
        ise = sum((r(:) - y).^2);
        
        % 超调量惩罚
        overshoot = max(0, (max(y) - 1) * 100);
        if overshoot > 5
            ise = ise * (1 + overshoot/20);
        end
        
        fitness = 1/(ise + 1e-6);
    catch
        fitness = 1e-6;
    end
end

终端输出为：

Generation      Func-count        f(x)           f(x)    Generations
    1               60        0.002212        0.002941        0
    2               88        0.002212        0.002778        1
    3              116        0.002176        0.002576        0
    4              144        0.002176        0.002398        1
    5              172         0.00217        0.002355        0
    6              200        0.002164        0.002237        0
    7              228        0.002164         0.00228        0
    8              256        0.002102        0.002323        0
    9              284        0.002102        0.002233        1
   10              312        0.002092        0.002237        0
   11              340        0.002092        0.002231        1
   12              368        0.002092         0.00226        2
   13              396        0.002092        0.002231        3
   14              424        0.002092        0.002254        4
   15              452        0.002092        0.002275        5
   16              480        0.002092        0.002234        6
   17              508        0.002092        0.002216        7
   18              536        0.002092        0.002218        8
   19              564        0.002092        0.002206        9
   20              592        0.002092        0.002175       10
   21              620        0.002092        0.002142       11
   22              648        0.002092        0.002142       12
   23              676        0.002092        0.002169       13
   24              704        0.002092        0.002166       14
   25              732        0.002092        0.002126       15
   26              760        0.002092        0.002141       16
   27              788        0.002092        0.002203       17
   28              816        0.002092        0.002271       18
   29              844        0.002092        0.002269        0
   30              872        0.002092        0.002256        1

                                  Best           Mean      Stall
Generation      Func-count        f(x)           f(x)    Generations
   31              900        0.002092         0.00227        2
   32              928        0.002092        0.002145        3
   33              956        0.002092        0.002133        4
   34              984        0.002092        0.002179        5
   35             1012        0.002092         0.00213        6
   36             1040        0.002092         0.00211        7
   37             1068        0.002092        0.002201        8
   38             1096        0.002092        0.002229        9
   39             1124        0.002092        0.002261       10
   40             1152        0.002092        0.002267       11
   41             1180        0.002092        0.002276       12
   42             1208        0.002092        0.002263       13
   43             1236        0.002092        0.002312       14
   44             1264        0.002092        0.002277       15
   45             1292        0.002092        0.002201       16
   46             1320        0.002092        0.002133       17
   47             1348        0.002092        0.002191       18
   48             1376        0.002092        0.002202       19
   49             1404        0.002092        0.002206       20
   50             1432        0.002092        0.002127       21
Optimization terminated: maximum number of generations exceeded.
优化结果:
 Kp = 0.1524
 Ki = 0.1448
 Kd = 0.2019