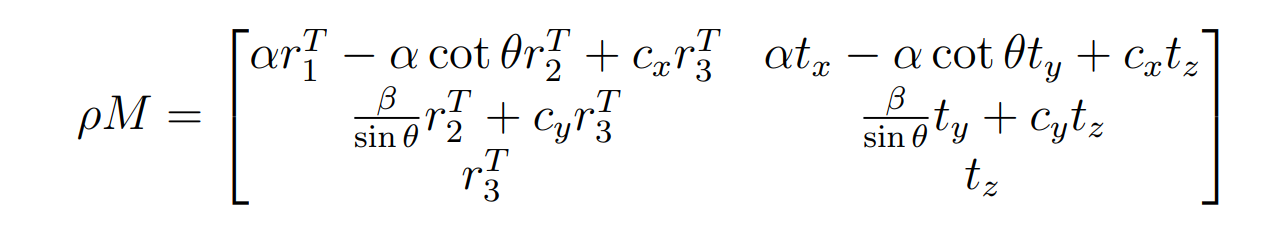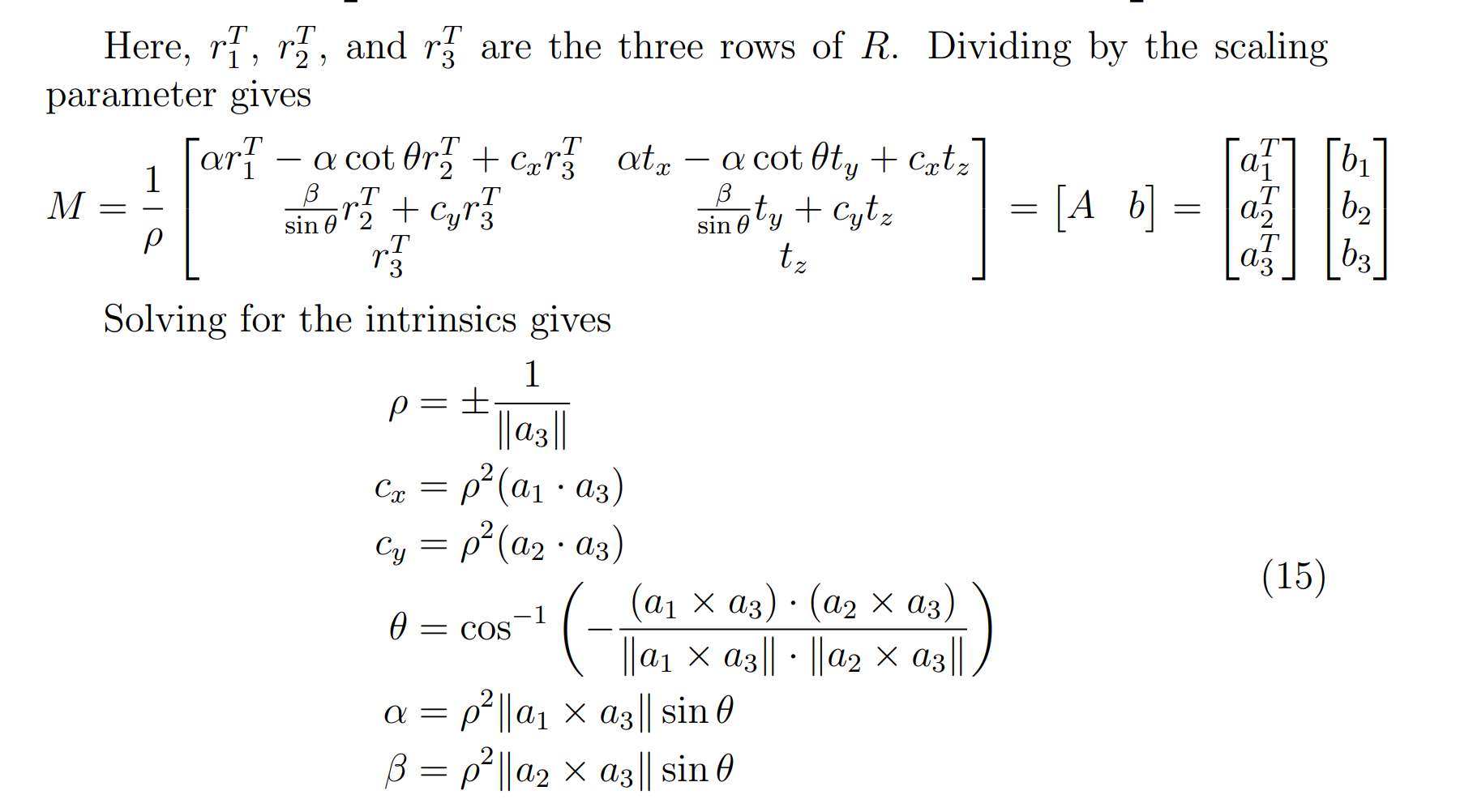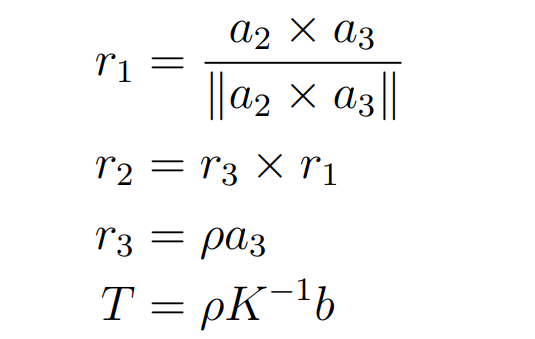相机模型
如果我们需要导航,在此之前我们需要一份相对详细的地图,那么视觉导航也是一样的,我们需要一个建图方法。对于机器人而言,视觉导航的关键在于相机的姿态和环境的深度信息。掌握这两点我们就可以进行建图了。
首先获取深度信息我们可以选择双目相机,结构光相机或者TOF相机等,通过一些简单的处理就可以获得相对准确的距离。如果使用单目相机,自然也是没关系的,我们也可以利用视差进行三角测量。相机的姿态也叫位姿,我们通过计算两帧图像特征点的差异得到本质矩阵,然后就可以还原前后的变化了。然后根据变换矩阵计算视差图,这样就可以实现和双目相机一样的算法了,只不过单目相机双帧有时差,而且位姿计算并不精确,所以难免会存在较高的误差。
为了解决这个问题,我们在计算单目相机的深度图时必须进行光心校正,我们知道相机成像是通过凸透镜成实像到CMOS上,但是这个凸透镜的中心并不完全在CMOS中心上,这使得成像中心并不在CMOS中心上,这个位移会在成像的图片上放大很多,这种情况就会产生成像畸变(包括桶形畸变和枕形畸变)所以在计算位姿时就必须考虑到这个问题。理论上相机成像可以理解为一个映射,把一个显示坐标映射到相平面即:
而这个P也可以写作下面的形式:
展开即为方程组:
其中的$c_x、c_y$就是凸透镜中心(也叫光心),这样校准相机就可以把相机给摸透了。
但是实际计算的P并不是在其他位置都是0,而是下面的形式:
其中的θ表示感光板的横边和纵边之间的角度,也就是CMOS与凸透镜径向的夹角(如下图)。
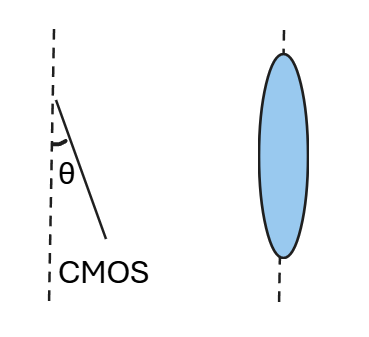
产生这个的原因很简单,凸透镜并不精细,边缘部分的焦距和这个方向并不一样,所以我们加入几个变量用于消除,而这个新的投影矩阵就是P’,解决办法很简单:
假设P’到P存在映射M,即:
在成像画面取各种特征点pi,均存在:
而$m_1、m_2、m_3$就是M的三行。我们把它变成线性方程的形式,即每个元素直接建立等式:
假设我们抽了n个变量,直接建立一个矩阵变化这个方程:
这样就变成了一个优化问题,只需要对这个P进行SVD,最优解就是D的最后一列(这个太超模了),截图发一发过程(选修)
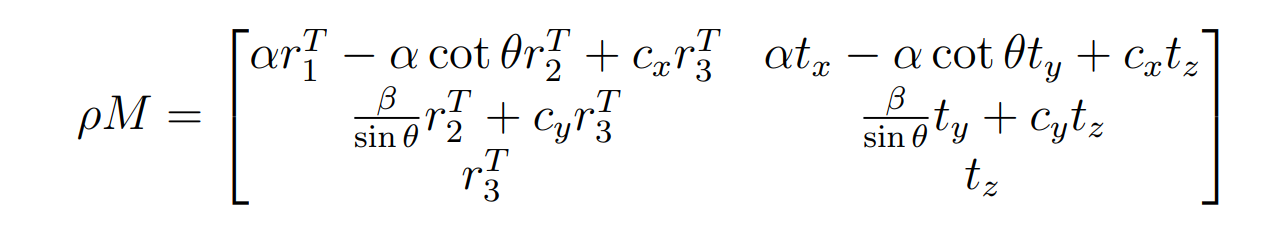
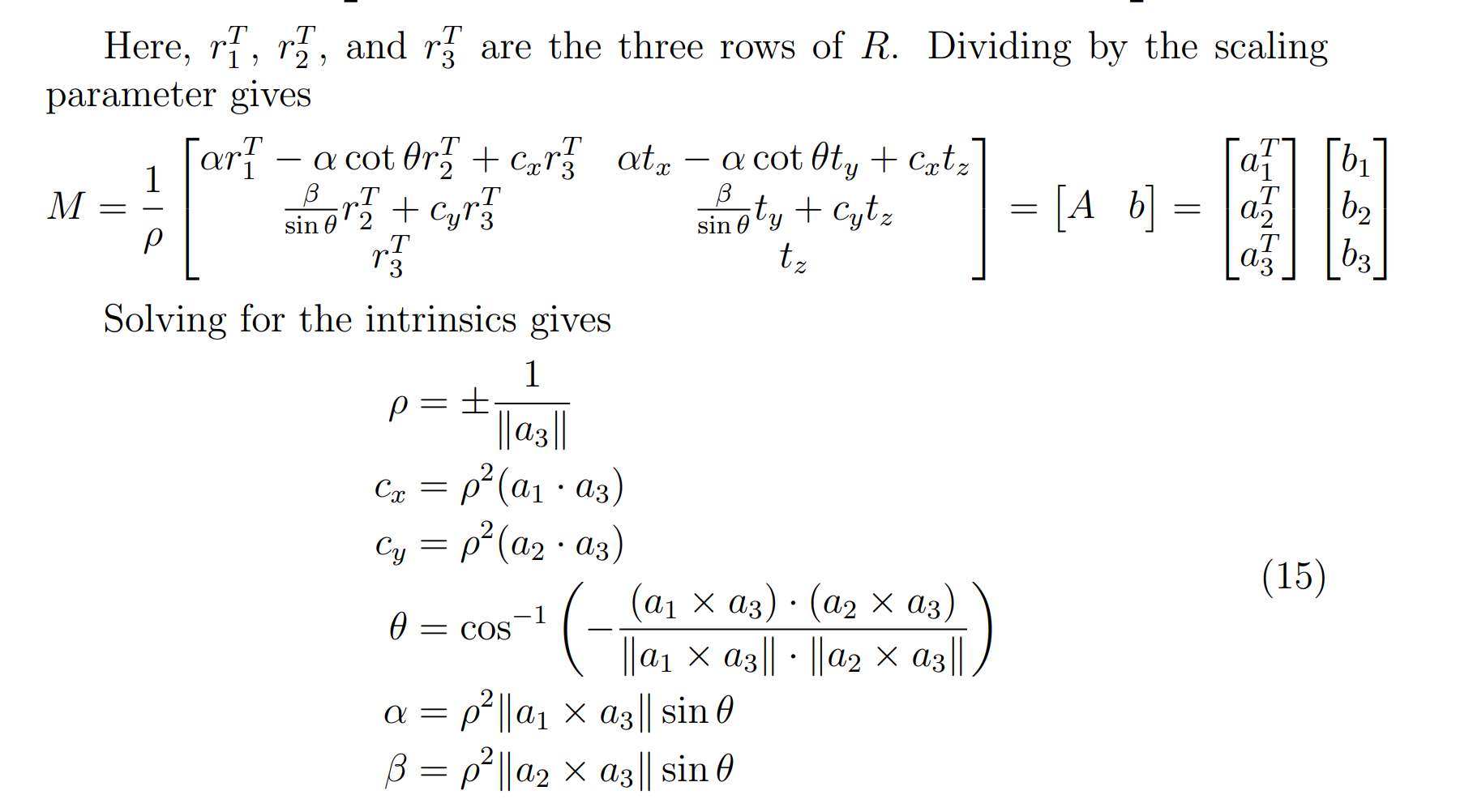
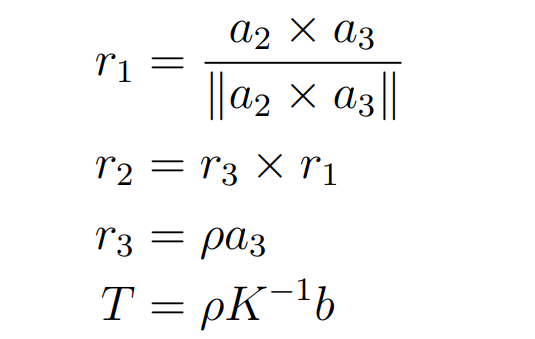
通过这个办法逐步收敛得到了矩阵K,而K就是内参矩阵,所以对于相机校准而言,图片必须要足够多:
提示:为什么相机标定需要标定板呢?答案很简单,我们通过计算角点得到标定板各个位置的坐标,以左上角为原点,各个点都有一个真实世界坐标,假设标定板的边长为W,那么各个点坐标都是(n×W,n×W,1)然后这些点当作真实世界坐标就可以放入上面的式子进行迭代优化了。
对极约束
对于相机而言,前后两帧存在变化:旋转和平移,即:
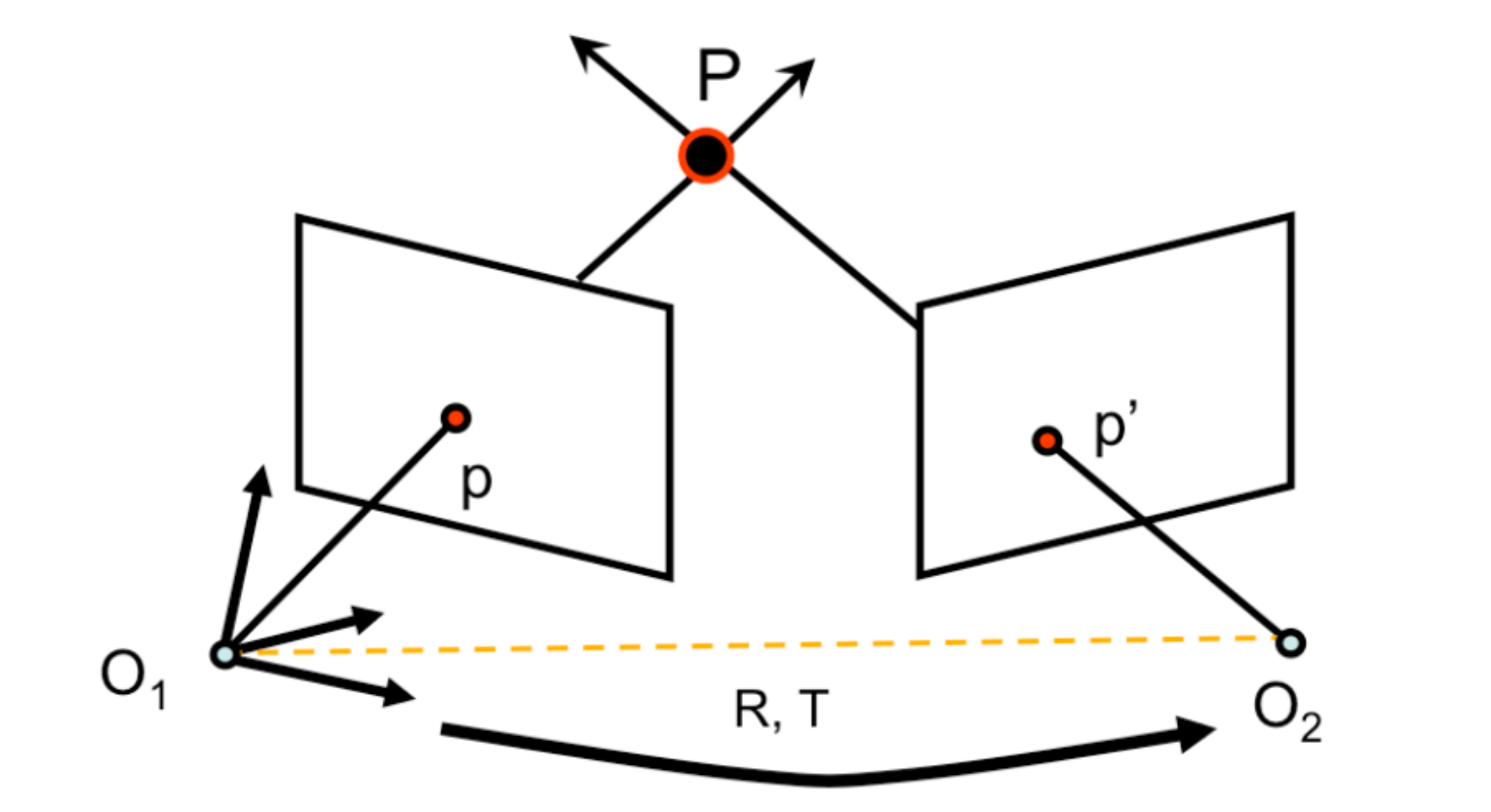
这里就不得不提及三幻神:F、E、H也就是基础矩阵,本质矩阵,和单应矩阵,这三幻神之间存在逐步递进的约束关系。
基础矩阵
本质矩阵就是描述两个图片之间关键点匹配后的关系,假设前后变化的点系为$x_2、x_1$,那么存在:
也就是两个图片的对极约束(上图中两帧不同的p与p’存在的约束)
求解F也非常简单,取出两帧的特征点(ORB、SIFT)利用RANSAC方法进行估计然后求解方程即可:
在此之前先补充一些知识:伪逆
假设有一个不可逆的矩阵A,我们希望求出一个满足下式条件的向量x:
我们不得不对A求逆,但是A不可逆只能求伪逆,伪逆求解过程如下:首先对A进行SVD分解
SVD分解如上式,A的SVD可以分解为三个变量,然后计算A的伪逆(因为A不一定可逆):
而:
也就是对奇异值矩阵非零的奇异值取倒数组成的矩阵。
这样就有左右同时乘伪逆就可以得出一个满足条件的特殊的x:
这个x也满足方程,仅此而已。
回归话题本身,求解基础矩阵只需要求:
对方程中的x展开特殊变量得到:
而u、v是x方向上的分量。通过求解A的伪逆就得到了特殊的F矩阵。
本质矩阵
本质矩阵是在已知相机内参的情况下,对两帧之间的特征点建立的关系即:
其中的K就是相机内参,F是基础矩阵。而E是平移量的反对称矩阵与旋转矩阵的乘积:
仅此而已,所以求出基础矩阵后就可以求出本质矩阵,进而恢复出相机的位姿。
这里举个代码的例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| void loadAndMatchImages(const cv::Mat& img1, const cv::Mat& img2, std::vector<cv::Point2f>& points1, std::vector<cv::Point2f>& points2) {
cv::Ptr<cv::ORB> detector = cv::ORB::create();
std::vector<cv::KeyPoint> keypoints1, keypoints2;
cv::Mat descriptors1, descriptors2;
detector->detectAndCompute(img1, cv::noArray(), keypoints1, descriptors1);
detector->detectAndCompute(img2, cv::noArray(), keypoints2, descriptors2);
cv::BFMatcher matcher(cv::NORM_HAMMING);
std::vector<cv::DMatch> matches;
matcher.match(descriptors1, descriptors2, matches);
for (const auto& match : matches) {
points1.push_back(keypoints1[match.queryIdx].pt);
points2.push_back(keypoints2[match.trainIdx].pt);
}
}
void recoverPose(const std::vector<cv::Point2f>& points1, const std::vector<cv::Point2f>& points2, const cv::Mat& K, cv::Mat& R, cv::Mat& t) {
cv::Mat E = cv::findEssentialMat(points1, points2, K);
int inliers = cv::recoverPose(E, points1, points2, K, R, t);
std::cout << "Inliers: " << inliers << std::endl;
}
|
然后简单调用就可以了:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| int main(){
cv::Mat img1 = cv::imread("img/img1.png");
cv::Mat img2 = cv::imread("img/img2.png");
cv::Mat K = (cv::Mat_<double>(3, 3) <<
308.5042733642555390, 0, 308.9428418257563749,
0, 306.0399135140206113, 229.3623543130335634
0, 0, 1);
std::vector<cv::Point2f> points1, points2;
loadAndMatchImages(img1, img2, points1, points2);
cv::Mat R, t;
recoverPose(points1, points2, K, R, t);
std::cout << "Rotation Matrix:\n" << R << std::endl;
std::cout << "Translation Vector:\n" << t << std::endl;
}
|
单应矩阵
单应矩阵也很简单理解,就是对两个图像的关键点进行映射的矩阵H即:
求解H后就可以用于同一场景的平面点之间的变换,适合用于图像配准和拼接等场景。两帧图像就可以无缝衔接到一起了。
举几个例子,这是一个使用ORB特征点计算单应矩阵得到H的算法,最终把两个图片拼接到一起的方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| void stitch(Mat &img1, Mat &img2, Mat &result){
Mat gray1, gray2;
cvtColor(img1, gray1, COLOR_BGR2GRAY);
cvtColor(img2, gray2, COLOR_BGR2GRAY);
Ptr<ORB> orb = ORB::create();
std::vector<cv::KeyPoint> kp1, kp2;
Mat des1, des2;
orb->detectAndCompute(gray1, Mat(), kp1, des1);
orb->detectAndCompute(gray2, Mat(), kp2, des2);
BFMatcher matcher(NORM_HAMMING);
std::vector<DMatch> matches;
matcher.match(des1, des2, matches);
double min_dist = 10000, max_dist = 0;
for (int i = 0; i < des1.rows; i++) {
double dist = matches[i].distance;
if (dist < min_dist) min_dist = dist;
if (dist > max_dist) max_dist = dist;
}
std::vector<cv::DMatch> goodMatches;
for (int i = 0; i < des1.rows; i++) {
if (matches[i].distance <= max(2 * min_dist, 28.0)) goodMatches.push_back(matches[i]);
}
std::vector<cv::Point2f> pts1, pts2;
for (size_t i = 0; i < goodMatches.size(); i++) {
pts1.push_back(kp1[goodMatches[i].queryIdx].pt);
pts2.push_back(kp2[goodMatches[i].trainIdx].pt);
}
Mat H = findHomography(pts2, pts1, RANSAC);
Mat imgWrap;
cv::warpPerspective(img2, imgWrap, H, cv::Size(img1.cols + img2.cols, img1.rows));
cv::imshow("imgWrap", imgWrap);
cv::waitKey(0);
}
|
VIO
这里介绍一下视觉里程计,我们通过一步一步计算本质矩阵E,一步一步还原位姿,我们就可以还原出一段连续变化的过程并绘制相机的路径图,而每两帧之间存在对级约束,又可以进行测距,这里写一下单目测距算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| void loadAndMatchImages(const cv::Mat& img1, const cv::Mat& img2, std::vector<cv::Point2f>& points1, std::vector<cv::Point2f>& points2) {
cv::Ptr<cv::ORB> detector = cv::ORB::create();
std::vector<cv::KeyPoint> keypoints1, keypoints2;
cv::Mat descriptors1, descriptors2;
detector->detectAndCompute(img1, cv::noArray(), keypoints1, descriptors1);
detector->detectAndCompute(img2, cv::noArray(), keypoints2, descriptors2);
cv::BFMatcher matcher(cv::NORM_HAMMING);
std::vector<cv::DMatch> matches;
matcher.match(descriptors1, descriptors2, matches);
for (const auto& match : matches) {
points1.push_back(keypoints1[match.queryIdx].pt);
points2.push_back(keypoints2[match.trainIdx].pt);
}
}
|
单目深度估计就可以用R变化先一帧,利用t的参数做极线进行三角测距:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| void estimateDepth(const std::vector<cv::Point2f>& points1, const std::vector<cv::Point2f>& points2, const cv::Mat& K, const cv::Mat& E, std::vector<cv::Point3f>& points3D) {
cv::Mat R, t;
cv::recoverPose(E, points1, points2, K, R, t);
cv::Mat P1 = K * cv::Mat::eye(3, 4, CV_64F);
cv::Mat P2 = K * (cv::Mat_<double>(3, 4) << R, t);
for (size_t i = 0; i < points1.size(); ++i) {
cv::Mat X;
cv::triangulatePoints(P1, P2, points1[i], points2[i], X);
X /= X.at<double>(3);
points3D.push_back(cv::Point3f(X.at<double>(0), X.at<double>(1), X.at<double>(2)));
}
}
|
为了看起来美观,这里加一个深度图绘制:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| void createDepthMap(const std::vector<cv::Point3f>& points3D, cv::Mat& depthMap, int width, int height) {
depthMap = cv::Mat::zeros(height, width, CV_32FC1);
for (const auto& point : points3D) {
int x = static_cast<int>(point.x);
int y = static_cast<int>(point.y);
if (x >= 0 && x < width && y >= 0 && y < height) {
depthMap.at<float>(y, x) = point.z;
}
}
cv::normalize(depthMap, depthMap, 0, 255, cv::NORM_MINMAX);
depthMap.convertTo(depthMap, CV_8UC1);
}
|
注意使用这个算法必须使用完全体的opencv即包括扩展包(有cuda默认会cuda加速,非常好用)
单目测距后绘制曲线需要可视化,因为我不会openGL所以我就不写了,放一段其他人的代码吧:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void recoverCameraMotion(const cv::Mat& E, const std::vector<cv::Point2f>& points1, const std::vector<cv::Point2f>& points2, const cv::Mat& K, std::vector<cv::Mat>& positions) {
cv::Mat R, t;
cv::recoverPose(E, points1, points2, K, R, t);
cv::Mat position = -R.t() * t;
positions.push_back(position);
glBegin(GL_LINE_STRIP);
for (const auto& pos : positions) {
glVertex3f(pos.at<double>(0), pos.at<double>(1), pos.at<double>(2));
}
glEnd();
}
|
双目测距写过很多了,懒得写了,直接上链接:
https://blog.minloha.cn/posts/21114578a6af8a2023031110.html
双目的位姿恢复和单目一样,就是用左眼或者右眼的图像进行计算本质矩阵E,然后恢复R与t。
位姿图的计算存在一些小误差,这里可以用梯度下降法进行优化,这样可以大大节省空间。假定变化位姿为T,使用对数映射求出T的李代数:
求导就可以用左扰模型进行计算,定义误差e:
而这个方程可以引入两个李代数即先后变化的两个位姿:
这里涉及了很多李代数的知识,可以通过阅读往期内容学会:
https://blog.minloha.cn/posts/1913234bff8c4f2024021323.html
这里缺失了一些些知识,也就是对状态估计的公式证明:



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| struct PoseGraphError {
PoseGraphError(const Eigen::Vector3d& observed) : observed_(observed) {}
template <typename T>
bool operator()(const T* const pose1, const T* const pose2, T* residuals) const {
Eigen::Map<const Eigen::Matrix<T, 3, 1>> p1(pose1);
Eigen::Map<const Eigen::Matrix<T, 3, 1>> p2(pose2);
Eigen::Matrix<T, 3, 1> error = p2 - p1 - observed_.cast<T>();
residuals[0] = error[0];
residuals[1] = error[1];
residuals[2] = error[2];
return true;
}
private:
Eigen::Vector3d observed_;
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void optimizePoseGraph(std::vector<Eigen::Vector3d>& poses, const std::vector<Eigen::Vector3d>& observations) {
ceres::Problem problem;
for (size_t i = 0; i < poses.size() - 1; ++i) {
problem.AddParameterBlock(poses[i].data(), 3);
problem.AddParameterBlock(poses[i + 1].data(), 3);
ceres::CostFunction* cost_function =
new ceres::AutoDiffCostFunction<PoseGraphError, 3, 3, 3>(
new PoseGraphError(observations[i]));
problem.AddResidualBlock(cost_function, nullptr, poses[i].data(), poses[i + 1].data());
}
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_SCHUR;
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
std::cout << summary.FullReport() << std::endl;
}
|
这个方法需要g2o库才可以运行。
通过这些方法就可以建图啦!
总结
本期博客的前置内容很多,需要按照顺序一步一步学习才可以学会,共勉
下面是之前写过的一点点笔记可以对付看看。