学会神经网络[3]——强化学习与脉冲神经网络

介绍本期内容

在之前我们介绍了强化学习的数学原理以及用tensorflow实现了DQN，那么本期我们的主要内容就是用pytorch实现一下DQN，首先我们需要复习一下什么是强化学习：

对于一些模糊对象的适应性学习，我们无法针对数学模型进行优化，人们通过自身经验性学习的策略给出了强化学习方法，即：计算机通过学习步骤的价值或收益进行优化学习，从而趋近最优解的一种方法。对于这种方法我们叫做强化学习

在22年的11月2日晚，我写了一篇关于强化学习的数学基础：强化学习基础超链接。这部分我们需要实现的DQN就是基于Q学习方法的数学原理进行实现的。

脉冲神经网络通过模拟神经元电信号的变化，进行数学估计信号，然后进行序列预测

然后我们需要实现一个脉冲神经网络的结构进行序列预测：脉冲神经网络超链接，进行简单的序列学习。

好的，介绍性的内容就是这么多，那么我们就开始实现本期博客的内容。

DQN

首先我们需要明白我们所做的内容是什么，DQN是通过深度神经网络去模拟经验的获取函数，让它可以给入一个系统状态，返回一个价值，通过比较价值的最优去进行学习，在切实采取模型输出的动作之后得到一个参考价值，然后进行学习。说白了，DQN就是在利用价值学动作，那么我们就可以模拟出下图：

1

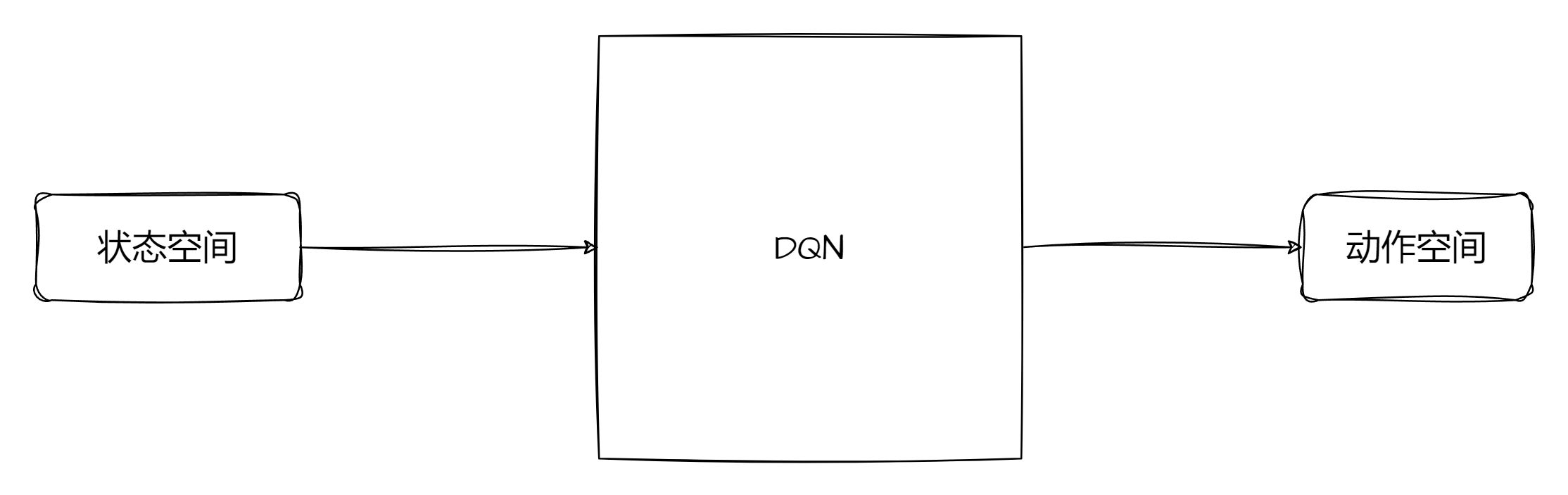
而Q学习有一个极大的缺点，那就是如果动作空间非常大，我们的Q表格也会变得很大，学习速度将会被拖垮。所以我们的DQN其实就是在模拟Q表格的过程。动作空间取决与外界环境，价值仅为一个向量即可。接下来实现模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
'''
@:param state_dim: 状态空间，取决于gym的状态空间
@:param action_dim: 动作空间, 取决于gym的动作数量
'''

class DQN(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(DQN, self).__init__()
        self.fc1 = nn.Linear(state_dim, 64)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Linear(64, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

当然，如果你的输入是图片的话也是可以的。然后我们需要实现一个MemoryPool，这里我们一般叫他经验回放池。其中需要有推入经验和随机取样经验的方法。这样我们的学习能力可以得到较大幅度的提高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class MemoryPool:
    def __init__(self, capacity):
        self.capacity = capacity
        self.memory = []
        self.position = 0

    def push(self, transition):
        if len(self.memory) < self.capacity:
            self.memory.append(None)
        self.memory[self.position] = transition
        self.position = (self.position + 1) % self.capacity

    def sample(self, batch_size):
        return random.sample(self.memory, batch_size)

    def __len__(self):
        return len(self.memory)

实现DQN时我们需要考虑一个问题就是震荡，也就是探索体在价值边界游走震荡的情况，为了解决这个问题我们一般会引入两个一模一样的DQN，分别叫做目标网络和探索体，探索体负责探索价值采取动作，直接学习，而目标网络是在探索体的基础上学习的，学习内容更加稳定。

1
2
3
4
5
6
7
8
import random
import torch
import torch.nn as nn
import torch.nn.functional as F
import gym

# 程序顶部加入
torch.cuda.set_device(0)

接下来就是我们的学习方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
'''
@:param env: gym环境
@:param policy_net: 探索体
@:param target_net: 目标网络
'''

def dqn_learning(env, policy_net, target_net, num_episodes=100, batch_size=64, gamma=0.99, epsilon=0.1, target_update=10):
    target_net.load_state_dict(policy_net.state_dict())
    # 不更新目标网络的梯度
    target_net.eval()
    # 使用Adam方法优化
    optimizer = torch.optim.Adam(policy_net.parameters())
    # 经验池与num_episodes一样大
    memory_pool = MemoryPool(100)
    # 奖励
    rewards = []
    for episode in range(num_episodes):
        state = env.reset()
        # 获取env环境状态
        state = torch.tensor(state[0], dtype=torch.float32)
        # 总奖励
        total_reward = 0
        while True:
            # epsilon贪婪策略
            if random.random() < epsilon:
                action = env.action_space.sample()
            else:
                with torch.no_grad():
                    action = policy_net(state).argmax().item()
            # 获取下一个状态
            res = env.step(action)
            next_state, reward, done, _, _ = res
            next_state = torch.tensor(next_state, dtype=torch.float32)
            # 计算总奖励
            total_reward += reward
            # 将状态存入经验池
            memory_pool.push((state, action, next_state, reward, done))
            state = next_state
            # 经验存放数量足够多时
            if len(memory_pool) > batch_size:
                # 从经验池中随机取出batch_size个经验
                transitions = memory_pool.sample(batch_size)
                batch = list(zip(*transitions))
                state_batch = torch.stack(batch[0])
                action_batch = torch.tensor(batch[1], dtype=torch.int64)
                next_state_batch = torch.stack(batch[2])
                reward_batch = torch.tensor(batch[3], dtype=torch.float32)
                done_batch = torch.tensor(batch[4], dtype=torch.float32)
                # 探索体计算Q值
                q_values = policy_net(state_batch).gather(1, action_batch.unsqueeze(1)).squeeze(1)

                with torch.no_grad():
                    # 目标网络计算下一个状态的Q值
                    next_q_values = target_net(next_state_batch).max(1)[0]
                    # 计算目标Q值
                    target_q_values = reward_batch + gamma * (1 - done_batch) * next_q_values
                # 计算探索体与目标网络的损失(分开独立训练学习)
                loss = F.mse_loss(q_values, target_q_values)
                optimizer.zero_grad()
                loss.backward()
                optimizer.step()
            if done:
                break
        # 追加奖励
        rewards.append(total_reward)
        if episode % target_update == 0:
            # 更新目标网络
            target_net.load_state_dict(policy_net.state_dict())
        if episode % 10 == 0:
            # 每10次输出一次奖励
            print('Episode:', episode, 'Reward:', total_reward)

这个方法实现后我们再来一个测试方法，用于检验我们的DQN学习情况的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def testEnv(env, policy_net):
    # 测试环境
    state = env.reset()
    # env显示图形界面
    env.render()
    state = torch.tensor(state[0], dtype=torch.float32)
    total_reward = 0
    # 不断循环
    while True:
        with torch.no_grad():
            action = policy_net(state).argmax().item()
        res = env.step(action)
        next_state, reward, done, _, _ = res
        next_state = torch.tensor(next_state, dtype=torch.float32)
        total_reward += reward
        state = next_state
        if done:
            break
    # 输出测试奖励
    print('Test Reward:', total_reward)

最后就是main方法了：

1
2
3
4
5
6
7
8
9
if __name__ == '__main__':
    env = gym.make("CartPole-v0", render_mode="rgb_array")
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.n
    policy_net = DQN(state_dim, action_dim)
    target_net = DQN(state_dim, action_dim)
    dqn_learning(env, policy_net, target_net)
    testEnv(env, policy_net)

我们运行一下就会发现：

1
2
3
4
5
6
7
8
9
10
11
Episode: 0 Reward: 83.0
Episode: 10 Reward: 16.0
Episode: 20 Reward: 9.0
Episode: 30 Reward: 15.0
Episode: 40 Reward: 13.0
Episode: 50 Reward: 11.0
Episode: 60 Reward: 9.0
Episode: 70 Reward: 52.0
Episode: 80 Reward: 9.0
Episode: 90 Reward: 130.0
Test Reward: 141.0

价值是在曲线上升，这也符合我们的策略。

A3C

A3C算法全名：Asynchronous Advantage Actor-Critic。也就是异步优势AC，主要需要两个结构：actor&critic所以我们就先通过类实现这两个结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 探索体身份(用于在环境测试学习)
class Actor(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(Actor, self).__init__()
        # 输入是状态空间尺寸
        self.fc1 = nn.Linear(state_dim, 64)
        self.fc2 = nn.Linear(64, 64)
        # 输出是动作
        self.fc3 = nn.Linear(64, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.softmax(self.fc3(x), dim=0)
        return x

探索体顾名思义就是在环境中探索的对象，我们需要让它可以输入一个状态输出一个动作。而评估体替代了DQN中的Q表格，使用单独的网络去拟合价值，这样我们就可以应对各种未知情况下的价值获取了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Critic(nn.Module):
    def __init__(self, state_dim):
        super(Critic, self).__init__()
        # 输入是一个状态
        self.fc1 = nn.Linear(state_dim, 64)
        self.fc2 = nn.Linear(64, 64)
        # 输出一个价值(数字)
        self.fc3 = nn.Linear(64, 1)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

然后用一个普通的类实现train和test方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class A3C:
    def __init__(self, state_dim, action_dim):
        self.actor = Actor(state_dim, action_dim)
        self.critic = Critic(state_dim)
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=0.01)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=0.01)

    def train(self, env, max_episode=100):
        for episode in range(max_episode):
            state = env.reset()
            state = torch.tensor(state[0], dtype=torch.float32)
            total_reward = 0
            while True:
                # 采样动作
                with torch.no_grad():
                    action = self.actor(state).argmax().item()
                res = env.step(action)
                # 放入预取动作，返回价值和状态
                next_state, reward, done, _, _ = res
                next_state = torch.tensor(next_state, dtype=torch.float32)
                total_reward += reward
                # 计算时序差分误差TD_error
                with torch.no_grad():
                    td_target = reward + 0.9 * self.critic(next_state)
                    td_error = td_target - self.critic(state)
                # 计算actor损失
                actor_loss = -torch.log(self.actor(state)[action]) * td_error
                # 计算critic损失
                critic_loss = F.mse_loss(self.critic(state), td_target)

                # 更新actor
                self.actor_optimizer.zero_grad()
                actor_loss.backward()
                self.actor_optimizer.step()
                # 更新critic
                self.critic_optimizer.zero_grad()
                critic_loss.backward()
                self.critic_optimizer.step()
                state = next_state
                if done:
                    break
            print('Episode:', episode, 'Reward:', total_reward)

    def test(self, env):
        state = env.reset()
        state = torch.tensor(state[0], dtype=torch.float32)
        total_reward = 0
        while True:
            with torch.no_grad():
                action = self.actor(state).argmax().item()
            res = env.step(action)
            next_state, reward, done, _, _ = res
            next_state = torch.tensor(next_state, dtype=torch.float32)
            total_reward += reward
            state = next_state
            if done:
                break
        print('Reward:', total_reward)

最后实现一个环境进行学习训练即可：

1
2
3
4
5
6
7
8
9
10
11
def main():
    env = gym.make('CartPole-v0', render_mode="rgb_array")
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.n
    a3c = A3C(state_dim, action_dim)
    a3c.train(env)
    a3c.test(env)


if __name__ == "__main__":
    main()

运行一下看看效果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Episode: 0 Reward: 9.0
Episode: 1 Reward: 10.0
Episode: 2 Reward: 10.0
Episode: 3 Reward: 9.0
Episode: 4 Reward: 10.0
Episode: 5 Reward: 9.0
Episode: 6 Reward: 10.0
Episode: 7 Reward: 9.0
Episode: 8 Reward: 10.0
......
Episode: 93 Reward: 8.0
Episode: 94 Reward: 9.0
Episode: 95 Reward: 8.0
Episode: 96 Reward: 9.0
Episode: 97 Reward: 8.0
Episode: 98 Reward: 8.0
Episode: 99 Reward: 9.0
Reward: 10.0

SNN

SNN仅仅是MP的进阶结构，所以我们还是按照MP的全连接进行训练学习，在早期我们讲解过脉冲神经网络的数学原理这里给出一个超链接：脉冲神经网络

对于一个神经元必要的参数就是激活电压阈值和膜电压衰退。这部分的存在意义可以查看超链接。神经细胞的输入是一个向量，输出是一个等型向量，并不会影响尺寸，所以使用的话只需要声明调用即可，神经节点数完全无需考虑。

1
2
3
4
5
6
7
8
9
10
11
12
class SpikingNeuron(nn.Module):
    def __init__(self, threshold=1.0, decay=0.9):
        super(SpikingNeuron, self).__init__()
        self.threshold = threshold
        self.decay = decay
        self.membrane_potential = 0

    def forward(self, x):
        self.membrane_potential += x
        spike = (self.membrane_potential >= self.threshold).float()
        self.membrane_potential = self.membrane_potential * (1 - spike) * self.decay
        return spike

如此一来我们就有了一个神经细胞，接下来我们就在FNN中嵌入一层神经细胞：

1
2
3
4
5
6
7
8
9
10
11
12
class SNN(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(SNN, self).__init__()
        self.fc1 = nn.Linear(input_dim, 64)
        self.neuron = SpikingNeuron()
        self.fc2 = nn.Linear(64, output_dim)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.neuron(x)
        x = self.fc2(x)
        return x

然后按照惯例，我们写一个样本生成方法，这里打算完成输入内容之间有某种联系，神经网络进行预测。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def train(net, num_epochs, data_loader, loss, optimizer):
    for epoch in range(num_epochs):
        epoch_loss = 0
        correct = 0
        total = 0

        for X_batch, y_batch in data_loader:
            optimizer.zero_grad()
            outputs = net(X_batch)
            l = loss(outputs.view(-1), y_batch)
            l.backward()
            optimizer.step()

            epoch_loss += l.item()
            correct += ((outputs.view(-1) > 0) == y_batch).sum().item()
            total += y_batch.size(0)

        print(f'Epoch {epoch + 1}/{num_epochs}, Loss: {epoch_loss / total:.4f}, Accuracy: {correct / total:.4f}')

然后给出测试方法：

1
2
3
4
5
6
7
8
9
def test(net):
    # 生成测试数据
    X_test = torch.randn(100, 2)
    y_test = (X_test[:, 0] + X_test[:, 1] > 0).float()
    # 画出测试数据与预测数据
    plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap='cool')
    # 预测点画x
    plt.scatter(X_test[:, 0], X_test[:, 1], c=(net(X_test) > 0).float().detach().numpy(), marker='x')
    plt.show()

最后就是main函数，我们多一些数据样本用于学习，epoch给到10轮即可，效果以及非常不错了。

1
2
3
4
5
6
7
8
9
10
11
if __name__ == "__main__":
    torch.cuda.set_device(0)
    X = torch.randn(1000, 2)
    y = (X[:, 0] + X[:, 1] > 0).float()
    dataset = data.TensorDataset(X, y)
    data_loader = data.DataLoader(dataset, batch_size=100, shuffle=True)
    net = SNN(2, 1)
    loss = nn.BCEWithLogitsLoss()
    optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
    train(net, 20, data_loader, loss, optimizer)
    test(net)

然后运行看看效果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Epoch 1/20, Loss: 0.0057, Accuracy: 0.8270
Epoch 2/20, Loss: 0.0043, Accuracy: 0.8960
Epoch 3/20, Loss: 0.0034, Accuracy: 0.9200
Epoch 4/20, Loss: 0.0030, Accuracy: 0.9100
Epoch 5/20, Loss: 0.0027, Accuracy: 0.9150
Epoch 6/20, Loss: 0.0025, Accuracy: 0.9160
Epoch 7/20, Loss: 0.0024, Accuracy: 0.9150
Epoch 8/20, Loss: 0.0025, Accuracy: 0.9040
Epoch 9/20, Loss: 0.0022, Accuracy: 0.9180
Epoch 10/20, Loss: 0.0023, Accuracy: 0.9130
Epoch 11/20, Loss: 0.0021, Accuracy: 0.9170
Epoch 12/20, Loss: 0.0021, Accuracy: 0.9200
Epoch 13/20, Loss: 0.0020, Accuracy: 0.9260
Epoch 14/20, Loss: 0.0020, Accuracy: 0.9150
Epoch 15/20, Loss: 0.0020, Accuracy: 0.9110
Epoch 16/20, Loss: 0.0020, Accuracy: 0.9170
Epoch 17/20, Loss: 0.0019, Accuracy: 0.9180
Epoch 18/20, Loss: 0.0019, Accuracy: 0.9220
Epoch 19/20, Loss: 0.0019, Accuracy: 0.9150
Epoch 20/20, Loss: 0.0019, Accuracy: 0.9080

2

3

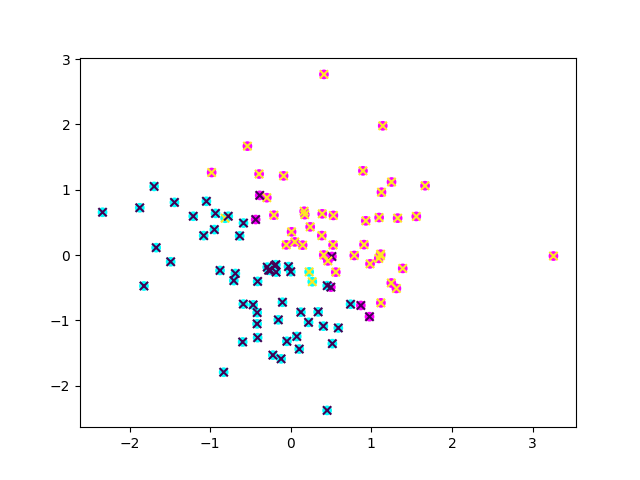
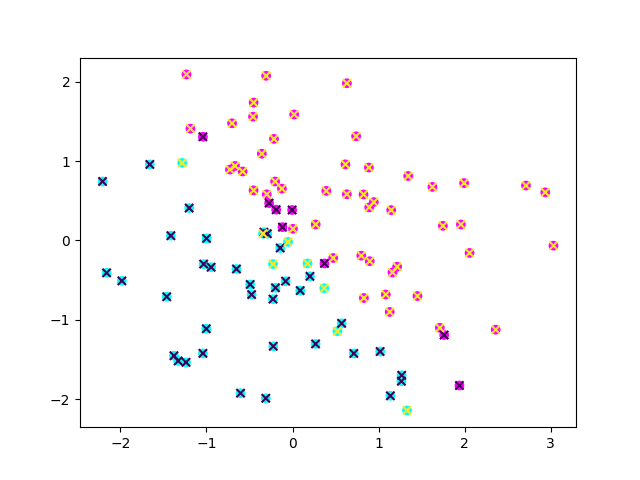
我这里运行两次，可以发现×几乎无偏的落在目标点上。可以看到SNN的效果还是可以的。

学会神经网络
#神经网络 #python
学会神经网络[3]——强化学习与脉冲神经网络
https://blog.minloha.cn/posts/211021ae243d902024031030.html
作者
Minloha
发布于
2024年3月10日
更新于
2024年9月15日
许可协议